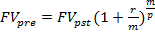Функция №4 – периодический взнос на погашение кредита (взнос на амортизацию единицы)

При рассмотрении функции №3 сложного процента «Текущая стоимость аннуитета» была выведена общая формула оценки текущей стоимости срочного аннуитета постнумерандо.

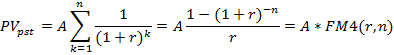
где 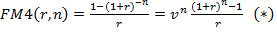- фактор текущей стоимости обычного аннуитета.

Обратную величину множителя, имеющую вид 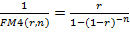называют фактором фонда обычной амортизации (функция сложного процента).

Из формулы (*) следует, что фактор фонда обычной амортизации равен величине периодического платежа, погашающего за n лет при заданной процентной ставке r основную сумму кредита в одну единицу и проценты за невозмещенную сумму (кредита). Причем платежи осуществляются в конце каждого года.

Временная оценка денежных потоков может поставить перед аналитиком проблему определения величины самого аннуитета, если известны его текущая стоимость, число взносов и ставка дохода.

Задача. Какую сумму можно ежегодно снимать со счета в течение пяти лет, если первоначальный вклад 1,5 тыс. руб. Банк начисляет ежегодно 10% при условии, что снимаемые суммы будут одинаковые.

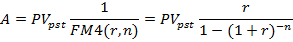
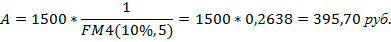
Таким образом, если положить на счет под 10% годовых 1,5 тыс. руб., то можно пять раз в конце года изъять со счета по 395 руб. 70 коп. Дополнительно полученные деньги в сумме 478,50 руб. (395,70 * 5 – 1500) является результатом начисления процентов на уменьшающийся остаток вклада.

Функция «периодический взнос на погашение кредита» является обратной по отношению к функции «текущая стоимость аннуитета».

Если текущая стоимость аннуитета равна произведению аннуитета и фактора текущей стоимости аннуитета, то определение величины аннуитета при помощи фактора текущей стоимости аннуитета возможно по формуле:

Аннуитет = Текущая стоимость аннуитета * (1 / Фактор текущей стоимости аннуитета).

Аннуитет может быть как поступлением (то есть входящим денежным потоком) так и платежом (то есть исходящим денежным потоком) по отношению к инвестору, поэтому данная функция может использоваться при необходимости для расчета величины равновеликого взноса в погашение кредита при заданном числе взносов и заданной процентной ставке. Такой кредит называется самоамортизирующимся.

Пример. Рассчитать величину ежегодного взноса в погашение кредита, предоставленного на 15 лет под 12% годовых в сумме 40 тыс. руб.

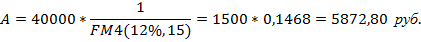
Заемщик уплатит кредитору за 15 лет 88092 руб. (5872,80*15), что превышает величину выданного кредита на 48092 руб. (88092-40000) Разница является результатом процентов, уплаченных заемщиком за пользование кредитом за весь период кредитования при условии, что основной долг постоянно уменьшается.

В разделе 4.3. была записана формула определения приведенной стоимости переменного аннуитета пренумерандо.

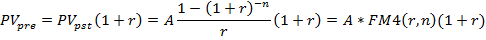
где 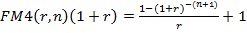- фактор текущей стоимости авансового аннуитета (множитель).

Обратную величину множителя 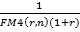называют фактором авансовой амортизации.

Фактор фонда авансовой амортизации равен величине периодического платежа, погашающего за n лет при заданной процентной ставке r основную сумму кредита в одну единицу и проценты за невозмещеную сумму (кредита). Причем платежи осуществляются в начале каждого года.

4.5. Функция 5 – будущая стоимость аннуитета (наращение – прямая задача)

Прямая задача предполагает оценку с позиции будущего, т.е. на конец периода n, когда реализуется схема наращения

С1

С2

С3

..........

Сn-1

Cn

Cn

Cn-1(1+r)

………….

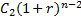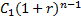На первое денежное поступление С₁ начисляются сложные проценты за (n-1)период и оно в конце n-го периода станет равным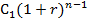

На второе денежное поступление С₂ начисляются сложные проценты за (n-2) периода и оно станет равным 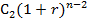и т.д.

На последнее денежное поступление C_n-1 проценты начисляются за один период и оно будет в конце n-го периода равно С_n-1(1+r).

На последнее денежное поступление Сn проценты не начисляются.

Следовательно, наращенный денежный поток для исходного потока постнумерандо имеет вид

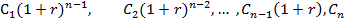
Будущая стоимость FV исходного денежного потока (аннуитета) постнумерандо может быть оценена как сумма наращенных поступлений

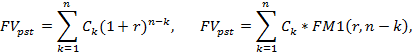
где FM1(r,n)=(1+r)ⁿ – множитель наращения.

Логика оценки аннуитета пренумерандо аналогична. Для прямой задачи схема наращения будет выглядеть следующим образом.

С1

С2

С3

..........

Cn

Cn(1+r)

………….

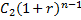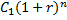n-1

n

Наращенный денежный поток имеет вид:

С₁(1+r)ⁿ, C₂(1+r)^n-1, …. , C_n(1+r)

Будущая стоимость аннуитета пренумерандо рассчитывается по форомуле

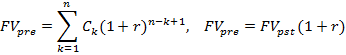
Оценка постоянного аннуитета постнумерандо

Аннуитет называется постоянным, если все денежные поступления равны между собой

С₁=С₂=С₃₌А

Прямая задача оценки срочного аннуитета при заданных величинах регулярного поступления (А) и процентной ставке r предполагает оценку будущей стоимости аннуитета (FV_pst).

Как следует из логики, присущей схеме аннуитета, записанный в порядке поступления платежей наращенный денежный поток (в аннуитет постнумерандо) имеет вид

А(1+r)^n-1, A(1+r)^n-2, ….. , A(1+r), A

Этот ряд представляет собой геометрическую прогрессию со знаменателем q=(1+r) и первым членом А. Число членов прогрессии равно n. Тогда будущая стоимость аннуитета равна сумме этой прогрессии

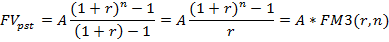
где 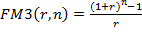– коэффициент наращения аннуитета.

Экономический смысл коэффициента наращения аннуитета заключается в том, что он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета.

Коэффициент наращения аннуитета показывает, во сколько раз наращенная сумма аннуитета больше величины денежного поступления А. В связи с этим его также называют коэффициентом аккумуляции вкладов или фактором будущей стоимости обычного аннуитета.

Если r – процентная ставка (в десятичных дробях) за базовый период, а начисление процентов происходит m раз в течение этого периода, то наращенный денежный поток, начиная с последнего денежного поступления имеет вид

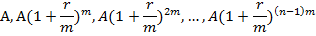
Получили геометрическую прогрессию, первый член которой равен А и знаменатель 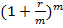. Сумма n первых членов этой прогрессии равна

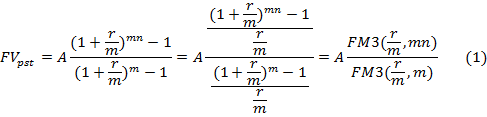
Ситуацию, когда в течение базового периода начисления процентов денежные поступления происходят несколько раз, а проценты начисляются один раз в конце периода, можно рассматривать с двух позиций.

1) Пусть в течение базового периода денежные поступления происходят р раз и один раз в конце периода начисляются проценты в соответствие со ставкой r.

Определим сумму, которая накопится к концу любого периода, если на отдельные взносы, поступающие в течение периода, начисляются сложные проценты.

На р-е поступление проценты не начисляются и оно остается равным А.

На предпоследнее (р-1) – е поступление начисляются сложные проценты за -ю часть периода и оно будет равно

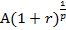
(в числителе 1,2 и т.д. до р-1 означает степень, в которую возводится множитель члена аннуитета)

На р-е поступление начисляются сложные проценты за -ю часть периода и оно будет равно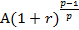

Полученная последовательность величин представляет собой геометрическую прогрессию с первым членом А, знаменателем 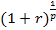и числом членов, равным р. Сумма этих величин равна:

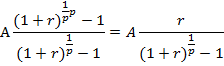
Т.о., можно считать, что имеем аннуитет в котором денежные поступления равны величине 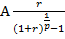и происходят в конце каждого базового периода начисления процентов. Поэтому получим:

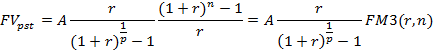
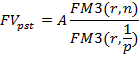
2) Пусть на отдельные взносы, поступающие в течение периода, начисляются простые проценты. Определим сумму, которая накопится к концу любого периода.

Последнее р-1 поступление равно А.

На предпоследнее (р-1)-е поступление начисляются простые проценты за -ю часть периода и оно будет равно .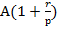

(p-2) – е поступление станет равным 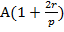и т.д.

Первое поступление станет равным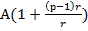

Полученные величины образуют арифметическую прогрессию, следовательно их сумма равна

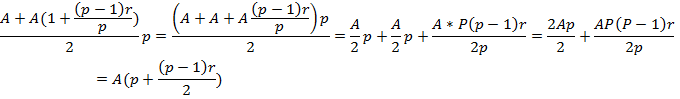
Аналогичным образом можно рассмотреть и самую общую ситуацию, когда в течение базового периода денежные поступления происходят р раз и проценты начисляются m раз за период. Например, если начисляются только сложные проценты, то как и ранее, определяем вначале сумму, образовавшуюся в конце любого периода.

Позднее р-е поступление в периоде остается равным А. Предпоследнее (р-1)-е поступление после начисления сложных процентов составит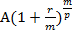

(р-2)-е поступление -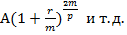

Находим сумму полученных величин

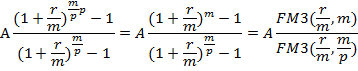
Cчитая, что есть аннуитет с денежными поступлениями, равными полученной сумме с использованием формулы (1) получим:

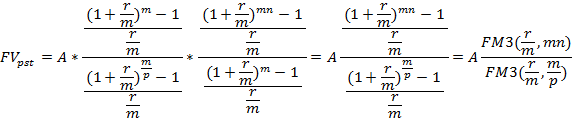
Оценка постоянного аннуитета пренумерандо

Т.к денежные поступления в аннуитете пренумерандо происходят в начале каждого периода, то этот аннуитет отличается от аннуитета постнумерандо количеством периодов начисления процентов.

Например, для срочного аннуитета пренумерандо с регулярными денежными поступлениями, равными А, и процентной ставкой r, наращенный денежный поток имеет вид:

Учитывая, что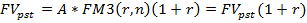

Т.е. наращенная сумма (будущая стоимость) аннуитета пренумерандо в (1+r) раз больше наращенной суммы постнумерандо.

Множитель 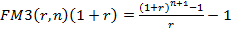называется фактором будущей стоимости авансового аннуитета.

Для аннуитета пренумерандо с начислением процентов m раз в течение базового периода, используя формулу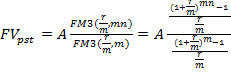

получим:

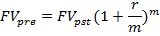
Пусть в течение базового периода денежные поступления происходят р раз. Тогда с учетом того, что 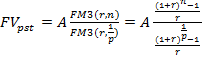можно записать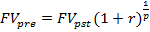

Пусть денежные поступления происходят р раз и проценты начисляются m раз за период. Тогда с учетом 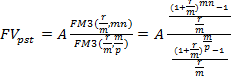можно записать