Определение текущей стоимости аннуитета

Обратная задача подразумевает оценку с позиции текущего момента, т.е. на конец периода. В этом случае реализуется схема дисконтирования, а расчет необходимо вести по приведенному потоку, все элементы которого с помощью дисконтных множителей приведены к настоящему моменту времени.

Элементы приведенного денежного потока можно суммировать. Их сумма характеризует приведенную или текущую стоимость аннуитета, которую при необходимости можно сравнивать с величиной первоначальной инвестиции.

Схема дисконтирования для исходного потока постнумерандо

С1

С2

С3

Сn-1

Сn

n-1

n

…….

………….

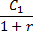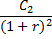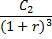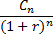Приведенный денежный поток для исходного потока постнумерандо имеет вид:

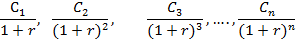
Приведенная стоимость денежного потока (аннуитета) постнумерандо рассчитывается по формуле:

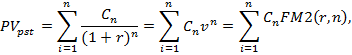
где 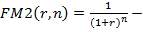множитель дисконтирования.

Оценка с позиции настоящего потока будущих доходов носит также название капитализации доходов.

Схема дисконтирования для исходного потока пренумерандо

С1

С2

С3

Сn-1

Сn

n-2

n-1

…….

С1

………….

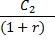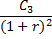n

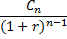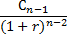Приведенный денежный поток для исходного потока пренумерандо имеет вид:

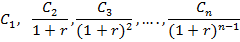
Приведенная стоимость потока пренумерандо рассчитывается по формуле:

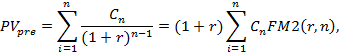
где 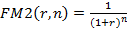- множитель дисконтирования.

PV_pre = PV_pst (1+r)

Оценка постоянного аннуитета постнумерандо

Производится оценка будущих денежных поступлений с позиции текущего момента, под которым в данном случае понимается момент времени, начиная с которого отсчитываются равные временные интервалы, входящие в аннуитет.

Член аннуитета равен А, срок аннуитета – n, дисконтирование ежегодное. В этих условиях дисконтированная величина:

первого платежа равна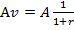

второго платежа равна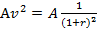

………

последнего платежа равна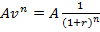

эти величины образуют ряд, соответствующий геометрической прогрессии с первым членом Av и знаменателем v.

Сумма членов этой прогрессии равна:

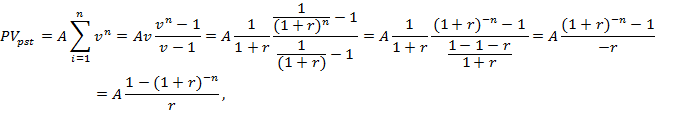
где 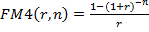- коэффициент дисконтирования аннуитета.

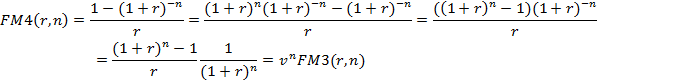
где 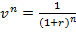- множитель дисконтирования,

А – член аннуитета,

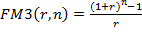- коэффициент наращения аннуитета.

Экономический смысл дисконтного множителя 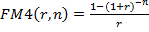заключается в следующем. Он показывает, чему равна с позиции текущего момента стоимость аннуитета с регулярными денежными поступлениями в размере одной денежной единицы (например, 1 рубль), продолжающегося n равных периодов с заданной процентной ставкой r.

Дисконтный множитель 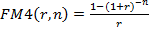называется фактором текущей стоимости обычного аннуитета (третья функция сложного процента).

Для постоянного аннуитета постнумерандо с начислением сложных процентов m раз за базовый период приведенный денежный поток имеет вид:

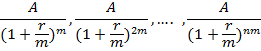
Следовательно сумма этих величин (приведенная стоимость аннуитета) равна (геометрическая прогрессия с членом 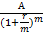и знаменателем ):

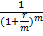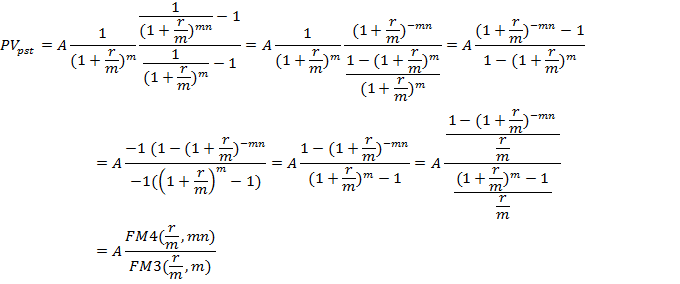
Таким образом: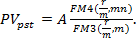

Для р- срочных аннуитетов с начислением сложных процентов один раз за базовый период формула определения текущей стоимости аннуитета выводится следующим образом.

Число членов аннуитета составляет np.

Величина первого платежа составляет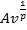

Величина второго платежа составляет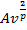

Величина последнего платежа составляет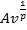

Первый член геометрической прогрессии равен 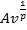, знаменатель геометрической прогрессии равен .

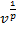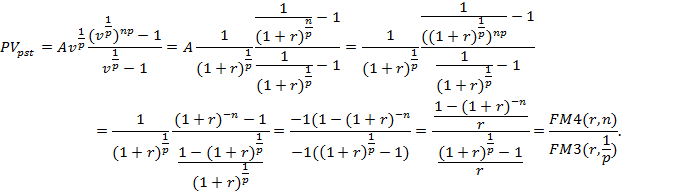
Таким образом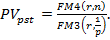

Для р- срочных аннуитетов с начислением сложных процентов m раз за базовый период формула имеет вид

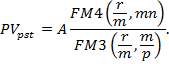
Проценты, полученные по учетной ставке называются антисипативными.

При антисипативном начислении процентов по сложной учетной ставке d наращенный денежный поток (при m=1, p=1), начиная с последнего денежного поступления, примет вид:

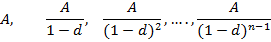
Следовательно: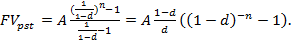

Бессрочный аннуитет.

Аннуитет называется бессрочным, если денежные поступления продолжаются достаточно длительное время. Математически это означает, что n→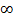

(пример бессрочного аннуитета –выпускаемые правительствами некоторых стран облигации, по которым производятся регулярные купонные выплаты, но которые не имеют фиксированного срока).

В этом случае прямая задача (определение будущей стоимости аннуитета) не имеет смысла. Имеет решение только задача об определении приведенной стоимости аннуитета.

Поток платежей в постоянном бессрочном аннуитете при одном денежном поступлении А за период, являющийся базовым для начисления процентов по ставке r, представляет собой бессрочно убывающую геометрическую прогрессию с первым членом 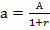и знаменателем .

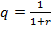Для бессрочного аннуитета постнумерандо используя формулу 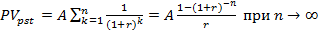получим:

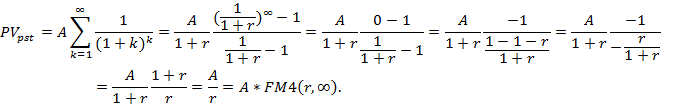
Таким образом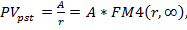

где FM4(r,n) =1/r.

Формула показывает, что поток с даже неограниченным числом платежей имеет все же конечную приведенную стоимость.

Из формулы 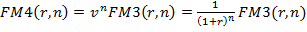следует:

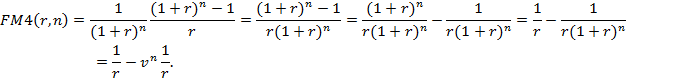
Если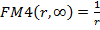

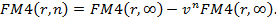
Пусть 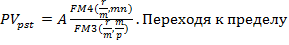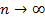, для бессрочного аннуитета постнумерандо с денежными поступлениями р раз за базовый период и начислением сложных процентов m раз за базовый период получим:

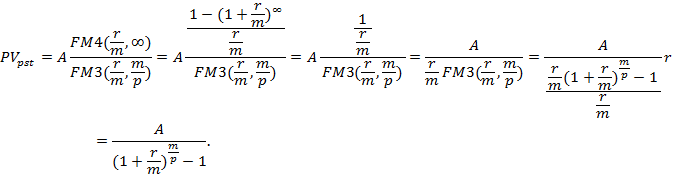
Приведенная стоимость бессрочно аннуитета пренумерандо в общем виде определяется с помощью приведенной стоимости бессрочного аннуитета постнумерандо по формуле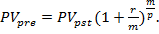

При р=1, m=1 из этой формулы следует (при ):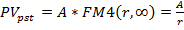

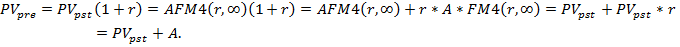
Таким образом приведенная стоимость бессрочного аннуитета пренумерандо отличается от таковой для постнумерандо на величину первого платежа.

Оценка постоянного аннуитета пренумерандо

Приведенная стоимость постоянного аннуитета пренумерандо определяется по формуле:

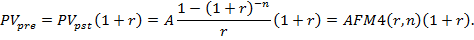
Приведенная стоимость постоянного р-срочного аннуитета пренумерандо определяется по формулам:

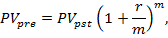
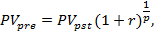
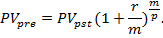
Иногда множитель 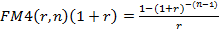называют фактором текущей стоимости авансового аннуитета.

В случае антисипативного начисления процентов формула для оценки аннуитета пренумерандо имеет вид:

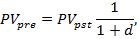
где d – учетная ставка.

Метод депозитной книжки

Суть метода. Сумма, положенная на депозит, приносит доход в виде процентов. При снятии с депозита некоторой суммы базовая величина, с которой начисляются проценты, уменьшается. Эта ситуация и имеет место в случае с аннуитетом.

Текущая стоимость аннуитета – это величина депозита с общей суммой причитающихся процентов, ежегодно уменьшающаяся на равные суммы.

Эта сумма годового платежа включает в себя начисленные за очередной период проценты, а также некоторую часть основной суммы долга. Таким образом, погашение исходного долга осуществляется постепенно в течение всего срока действия аннуитета.

Структура годового платежа постоянно меняется: в начальные периоды в нем преобладают начисленные за очередной период проценты. С течением времени доля процентных платежей постоянно уменьшается и повышается доля погашаемой части основного долга.

Интерпретация приведенной стоимости аннуитета с помощью метода депозитной книжки.

Пусть получена ссуда в сумме D₁=S на n лет под процентную ставку r. Сложные проценты начисляются на непогашенный остаток.

Определяем величину годового платежа при возврате долга равными суммами в конце каждого года.

Пусть А – годовой платеж.

В конце первого года часть годового платежа I₁=S*r идет на уплату процентов.

Оставшаяся часть H₁=A-S*r – идет на уплату части долга.

Таким образом на начало второго года величина непогашенного остатка:

D₂=S-(A-S*r)=S(1+r)-A=D₁(1+r)-A.

Аналогично остаток долга на начало k-го года связан остатком долга на начало предыдущего года следующим соотношением:

D_k=D_k-1(1+r)-A, (*)

Из этой формулы:

А=D_k-1*r + (D_k-1 – D_k) – годовой платеж.

где D_k-1*r - проценты, начисляемые на текущий долг,

D_k-1-D_k – сумма, идущая на погашение основного долга.

Если D₁=S, D₂=S(1+r)-A, то

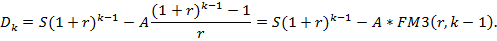
Т.к. долг должен быть выплачен через n лет, то D_n-1=0, т.е. справедливо равенство (k=n+1):

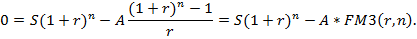
Из этого равенства следует:

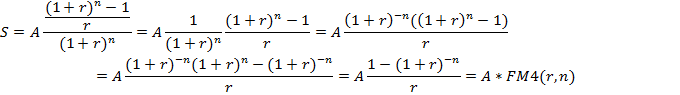
Следовательно S- приведенная стоимость постоянного аннуитета постнумерандо с членом, равным А, т.е.:

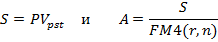
I_k=D_k*r – величина процентов за k-й год.

Умножая обе части (*) на r получим:

D_k*r=D_k-1(1+r)r-A*r,

т.е.I_k=I_k-1(1+r)-A*r (**)

Н_k=A-I_k – погашенная часть долга в k-м платеже.

Согласно (**) H_k=A-I_k-1(1+r)+A*r=(A-I_k-1)(1+r).

Таким образом

Н_k=H_k-1(1+r)

Из последней формулы видно, что суммы, идущие на погашение основного долга увеличиваются.