Простая и сложная ставка учетного процента

Начисление по простой учетной ставке процентов d используется при учете векселей и других денежных обязательств :

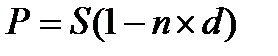, (4.16)

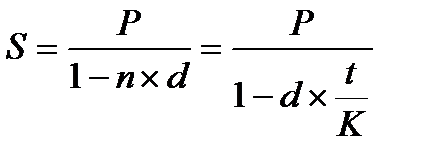. (4.17)

Простая учетная ставка d используется при дисконтировании по методу банковского учета. Например, выкупная цена (современная стоимость) векселя определяется по формуле

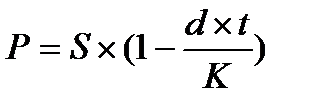, (4.18)

где t – срок, остающийся до погашения векселя, в днях.

Второй сомножитель этого выражения (1– d × t/К) называется дискон-тным множителем банковского учета по простым процентам. Как правило, при банковском учете применяются обыкновенные (коммерческие) проценты с точной длительностью ссуды (365/360).

Начисление по ставке сложных процентов 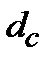относится к разряду финансовой экзотики:

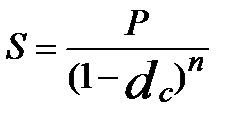, (4.19)

где 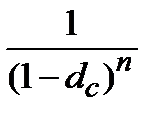– множитель наращения сложных антисипативных процентов.

Для начисления процентов m раз в году:

, (4.20)

где f – номинальная годовая учетная ставка при начислении m раз в году.

Эквивалентность процентных ставок

Эквивалентные процентные ставки – ставки разного вида, например простая годовая ставка ссудного процента и сложная годовая ставка ссудного процента, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.

Например:

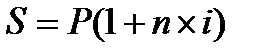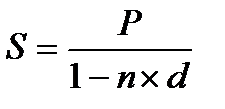Так как и , то .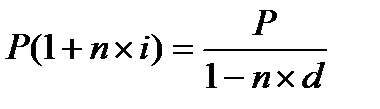

Следовательно, уравнение эквивалентности имеет вид:

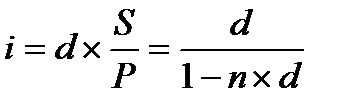, (4.21)

Соблюдая это условие, можно получать эквивалентные результаты, начисляя проценты как по формуле 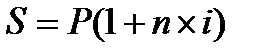, так и по формуле .

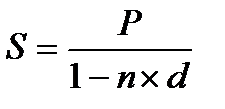Уравнения эквивалентности:

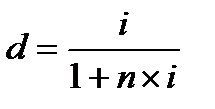, (4.22)

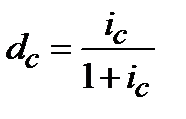, (4.23)

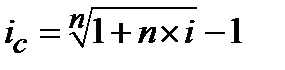, (4.24)

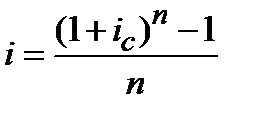, (4.25)

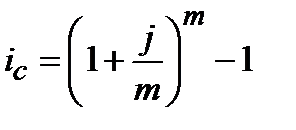, (4.26)

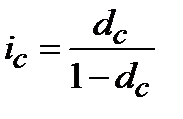. (4.27)

Уравнение эквивалентности – это соотношение, выражающее зависимость между процентными ставками различного вида.

Примеры построения графика платежей по кредиту

Рассмотрим расчет платежей по кредиту при различных вариантах погашения кредитов.

Платежи по кредиту в общем случае состоят из двух частей:

- погашение основной суммы долга – амортизация долга, то есть возмещение заемщиком суммы выданного кредита;

- уплата процентных денег за пользование кредитом, то есть плата за предоставление заемщику денег в долг.

Следует иметь в виду, что при расчете платежей по кредиту день получения кредита и день погашения кредита чаще всего учитываются как один день.

Выделяют следующие базовые варианты погашения кредита и уплаты процентов по нему:

1) погашение кредита равными частями с уплатой процентов по нему в конце каждого интервала начисления (декурсивный способ начисления процентов, простая ставка ссудного процента);

2) погашение кредита шаровым платежом: уплата процентов производится в конце каждого интервала начисления в течение всего срока действия кредитного договора, а погашение основной суммы долга – одним платежом в конце срока кредитования;

3) погашение кредита аннуитетными платежами: погашение основной суммы долга и уплата процентов осуществляются в конце каждого интервала начисления, но сумма кредитного платежа постоянная, то есть не меняется по интервалам.

Рассмотрим порядок построения платежей по первому варианту кредитования.

Пример 4.2. 3 марта привлечен кредит на 4 месяца в объеме 24 млн. руб. Процентная ставка 18 % годовых. Составить график платежей по кредиту с учетом точного количества дней в году.

Решение:

Рассчитаем сумму ежемесячного погашения основного долга, как отношение объема привлеченного кредита к количеству интервалов начисления, то есть 24 млн. руб. /4 месяца = 6 млн. руб.

Находим дневную процентную ставку 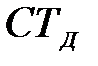делением годовой процентной ставки на точное количество дней в году.

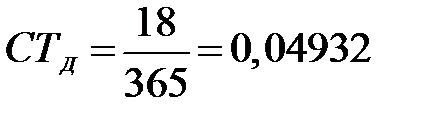% (или в долях от единицы 0,000493).

Примем в расчетах, что день получения кредита учитывается при начислении процентов, а за последний день пользования кредитом проценты не начисляются.

Построение графика платежей удобно проводить в форме таблицы.

Таблица 4.2 – График платежей по кредиту с ежемесячным погашением основной суммы долга и ежемесячной уплатой процентов по кредиту

Дата платежа	Остаток задолжен-ности по кредиту, млн. руб.	Количество дней начисления процентов	Составляющие кредитного платежа, млн. руб.	Общий платеж по кредиту (гр. 4 + гр. 5)
погашение основной суммы долга	процентные деньги по кредиту, гр. 2 × гр. 3 ×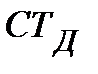
1 апреля за март		31 – 2 = 29		0,3431	6,3431
1 мая за апрель	24 – 6 = 18			0,2662	6,2662
1 июня за май	18 – 6 = 12			0,1834	6,1834
1 июля за июнь	12 – 6 = 6			0,0887	6,0887
Итого:				0,8815	24,8815

Таким образом, переплата по кредиту составила (0,8815 / 24) × 100 = = 3,67 %

При погашении кредита шаровым платежом остаток задолженности по кредиту равен первоначальной сумме кредита в течение всего периода кредитования. Поэтому проценты в каждом интервале кредитования начисляются на одну и ту же первоначальную сумму долга.

Ежемесячный платёж при аннуитетной схеме погашения кредита состоит из двух частей. Первая часть платежа – это процентные деньги за пользование кредитом. Вторая часть – погашение основной суммы долга. Аннуитетная схема погашения отличается от дифференцированной тем, что в начале кредитного периода проценты составляют большую часть платежа. Поэтому сумма основного долга уменьшается медленно, соответственно переплата процентов при такой схеме погашения кредита получается больше.

Расчет кредитных платежей при методе аннуитетных платежей проводится по формуле 4.28

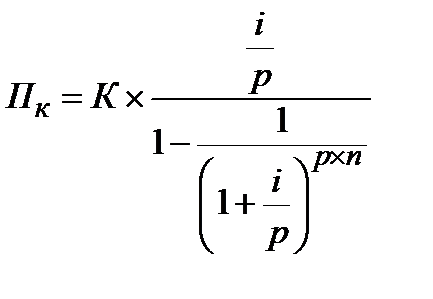, (4.28)

где 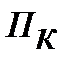– аннуитетный платеж по кредиту, руб.; К – сумма кредита, руб.; i – годовая процентная ставка по кредиту, в долях от единицы; р – количество кредитных платежей в одном году; n – срок кредитования, в годах.

Пример 4.3. Привлечен кредит в размере 6 млн. руб. сроком на 1 год. Погашение кредита и уплата процентнов осуществляются ежемесячно аннуитетными платежами. Построить график платежей по кредитному договору. Годовая ставка – 19,9 %.

Решение:

Определим ежемесячный аннуитетный платеж по кредиту по формуле 4.28.

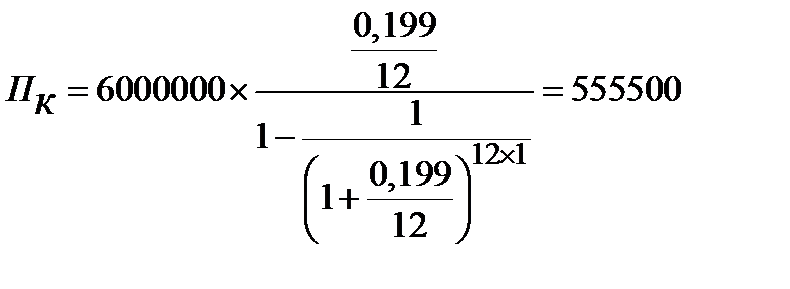руб.

Таблица 4.3 – Расчёт графика выплат по аннуитетному кредиту

Дата платежа	Остаток задолженности по кредиту, руб.	Составляющие кредитного платежа, млн. руб.	Общий платеж по кредиту (гр. 3 + гр. 4)
погашение основной суммы долга	процентные деньги по кредиту,
января	6 000 000	555 500 – 99 500 = = 456 000	6000 000 × 0,199/12 = = 99500	555 500
20 февраля	6 000 000 – – 456 000 = = 5 544 000	555500 – 91938 = = 46 3562	5544 000 × 0,199/12 = = 91 938	555 500
и т. д.

Как видно из результатов расчетов , особенностью данного вида кредитов является ежемесячное увеличение платежей по возврату основной суммы долга и уменьшение выплат по начисленным процентам.

Вопросы и задания по теме

1. Если вам предстоит по условиям финансового контракта получить определенную сумму денег через 4 года, какую (простую или сложную) ставку процентов вы предпочли бы использовать в расчетах, если бы столкнулись с необходимостью продать этот контракт и определить его сегодняшнюю стоимость?

2. Уменьшается ли приведенная стоимость денег с линейной скоростью, с нарас­тающей скоростью или с уменьшающейся скоростью при изменении продол­жительности времени до того момента в будущем, когда деньги должны быть получены? Почему?

3. «Правило 72» предполагает, что сумма на сберегательном счете удвоится за 12 лет при ежегодном начислении 6 % по методу сложных процентов (или за 6 лет при ежегодном начислении 12 %). Может ли это правило с успехом применять­ся на практике, какова его точность?

4. Рассматриваются два варианта помещения сбережений на депозит. В соответствии с первым каждые шесть месяцев будут помещаться на счет 10 тыс. руб. под 7 % годовых, начисляемых по методу сложных процентов каждые полгода. В соответствии со вторым вариантом каждый год помещаются на счет 20 тыс. руб. под 7,5 % годовых, начисляемых по методу сложных процентов каждый год. Первоначальный вклад, в соответствии с первым вариантом, помещается на сбе­регательный счет через шесть месяцев, а в соответствии со вто­рым вариантом – через год (отсчет времени ведется от настоящего момента).

А. Каким вариантом следует воспользоваться?

Б. Изменится ли ваш ответ на предыдущий вопрос, если процентная став­ка по второму варианту составит 7 % годовых?

5. В соответствии с финансовым контрактом вы имеете возможность получить либо 50 тыс. руб. через шесть лет, либо 100 тыс. руб. – через двенадцать лет. При какой процентной ставке (начисляемой ежегодно по методу сложных процентов) оба эти варианта окажутся для вас равноценными?

6. Банк предлагает приобрести семимесячный депозитный сертификат, по которому выплачиваются проценты в размере 7,06 % годовых, что обеспечит вам годовую эффективную доходность в размере 7,25 %. Определите, с какой периодичностью (ежедневно, еженедельно, ежемесячно или ежеквар­тально) начисляются проценты по депозитному сертификату?

7. Каким окажется по истечении пяти лет начальный депозит величиной $ 2500 при начислении сложных процентов (к тому же в конце каждого года на протяжении всех пяти лет производилась выплата в размере $ 50), если годовая процентная ставка рав­няется: 10 %, 5 %, 0 %?

8. Ваши родители решили, что в ка­ждый очередной день вашего рождения, начиная с того момента, когда Вам исполнилось три года, они будут помещать на предназначен­ный для вас сберегательный счет по $ 100 ежегодно. На сберегательный счет начисляются сложные проценты (4 % годовых). Вам исполнилось 18 лет, и вы хотите получить всю накопившуюся сумму. Однако оказывается, что в день Вашего 7-ми и 13-летия счет не пополнялся. Какая сумма накопится на этом сберегательном счете ко дню вашего 18-летия?

9. Предприятие собирается купить здание. С этой целью получен ипотечный кредит на 20 лет в размере, эквивалентном $ 120000. Ссудные проценты, выплачиваемые в соответствии с этим кредитом, составляют 6 % годовых, начисляемых по ставке сложных процентов. Погашение долга и выплата процентов производится ежегодно равными частями в течение 20 лет. Какова сумма ежегодных платежей?