Простая и сложная ставки ссудного процента

Начисление простых процентов при декурсивном способе производится по формуле

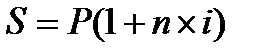или 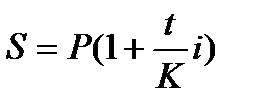, (4.7)

где n – продолжительность периода начисления в годах; t – продолжительность периода начисления процентов в днях; (1+n×i) – множитель наращения простых процентов. Он показывает, во сколько раз вырос первоначальный капитал; K – продолжительность года в днях (временная база для расчета процентов).

Если К = 360 дней, то рассчитывают обыкновенный (коммерческий) процент, если К = 365 или 366 дней, то говорят о точном расчете процентов. В свою очередь подсчет продолжительности периода начисления процентов (длительности ссуды) может быть приближенным или точным. Наиболее часто встречающиеся комбинации:

- точный расчет процентов с точной длительностью ссуды;

- коммерческие проценты с точным числом дней ссуды;

- обыкновенные проценты с приближенной длительностью ссуды.

Ставки процентов могут быть плавающие (переменные). В этом случае в каждом интервале начисления или в каждой группе интервалов начисление процентов производится по разным ставкам. Для банков – это способ минимизации рисков. Общая формула расчета будет иметь следующий вид:

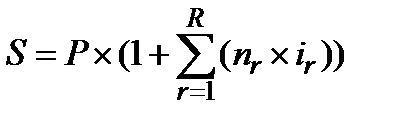, (4.8)

где R – общее число периодов, в течение которых проценты начисляются по неизменной ставке.

Простая процентная ставка i используется при математическом дисконтировании. Расчеты выполняются по формуле

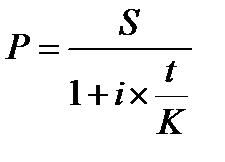. (4.9)

Выражение 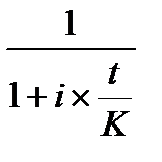называется дисконтным множителем математического дисконтирования по простым процентам.

Начисление сложных процентов при декурсивном способе:

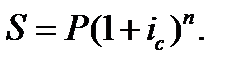(4.10)

Простые ставки ссудных процентов обычно применяются в краткосрочных финансовых операциях (до года).

Быстрый способ решения задач по удвоению капитала со сложными процентами получил название «Правило 72»: если 72 разделить на количество лет, в течение которых деньги будут находиться на депозите, то получится приблизительное значение процентной ставки i_c,которое требуется для того, чтобы сбережения удвоились. Полученный ответ не является точным, но позволяет получить результаты, достаточно близкие к точным значениям.

Если срок кредита в годах n не является целым числом, то расчет ведется по формуле 4.11.

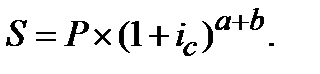(4.11)

Наиболее щепетильные кредиторы, принимая во внимание большую эффективность простых процентов на коротких отрезках времени, используют смешанный порядок начисления процентов в случае, когда срок операции (ссуды) не равен целому числу лет: сложные проценты начисляются на период, измеренный целыми годами, а проценты за дробную часть срока начисляются по простой процентной ставке. Смешанный порядок начисления процентов:

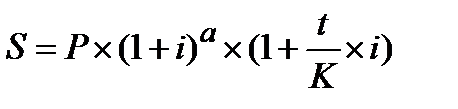, (4.12)

где a – число полных лет в составе продолжительности операции; t – число дней в отрезке времени, приходящемся на неполный год; K – временная база.

Если 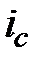будет различной на разных интервалах начисления, то

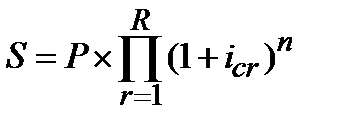. (4.13)

Важной особенностью сложных процентов является зависимость конечного результата от количества начислений в течение года, так как база начисления увеличивается после каждого интервала начисления. В связи с этим принято различать номинальную и эффективную годовые процентные ставки при начислении сложных процентов.

Номинальной (или объявленной)называется годовая сложная процентная ставка, указываемая применительно к периоду в один год и не корректируемая в соответствии с частотой начисления процентов. Эффективная годовая процентная ставка – фактическая процентная ставка, используемая после внесения в номинальную ставку поправки на такой фактор, как количество интервалов начисления процентов за год. Если проценты начисляются несколько раз в год, эффективная процентная ставка оказывается выше, чем номинальная.

Пример 3.1. Определить эффективную процентную ставку при начислении сложных процентов по 4 % ставке ежеквартально.

Решение:

Номинальная годовая ставка составляет: j = 4×4 = 16 % годовых.

При начислении по номинальной ставке процентов коэффициент наращения за год составит:

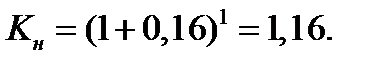
При начислении 4 раза в год по ставке 4 % ежеквартально коэффициент наращения за год

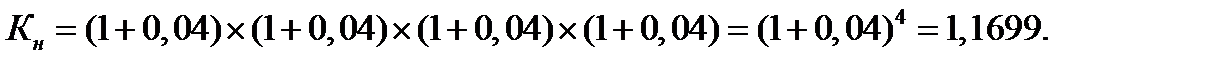
Следовательно, эффективная годовая ставка сложных процентов составит 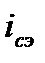=16,99 %.

Начисление сложных процентов при начислении их m раз в год ведется по формуле

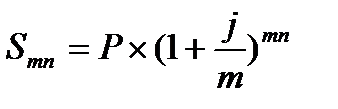, (4.14)

где j – номинальная ставка ссудного процента при начислении m раз в году.

Для расчета эффективной годовой процентной ставки можно воспользоваться формулой 4.15

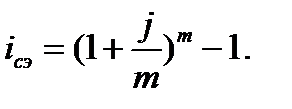(4.15)

Воспользуемся данными примера 4.1 для расчета эффективной процентной ставки

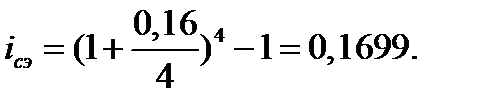
По мере увеличения частоты начислений в год разница между величиной номинальной и эффективной ставки будет возрастать.