Тема: Финансовая функция ПЛТ

Время выполнения - 3 часа.

Цель работы: научиться использовать финансовую функцию ПЛТ табличного процессора Microsoft Excel для решения экономических задач, с использованием представленных примеров.

Последовательность выполнения:

1.Решить все описанные упражнения самостоятельно, руководствуясь методическими указаниями;

2. Выполнить задание;

3. Проверить свои знания по контрольным вопросам и сдать лабораторную работу.

Основные сведения по теме:

Финансовая функция ПЛТ

Лист1 в книге ФИНАНСОВЫЙ АНАЛИЗ переименуйте в ПЛТ. Все упражнения в данной лабораторной работе выполняйте на листе ПЛТ.

Рассмотрим пример расчета 30-летней ипотечной ссуды со ставкой 8% годовых при начальном взносе 20% и ежемесячной (ежегодной) выплате с помощью функции ПЛТ.

Для приведенного на рис.4.1.1 ипотечного расчета в ячейки введены формулы, показанные на рис. 4.1.2.

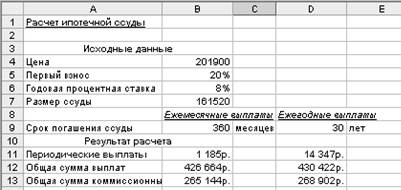
Рис. 4.1.1 Расчет ипотечной ссуды

Введите представленные на рис. 4.1.2. данные на лист ПЛТ и сравните полученный результат с данными на рис. 4.1.1.

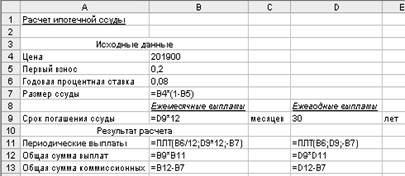
Рис. 4.1.2 Формулы для расчета ипотечной ссуды

Функция ПЛТ вычисляет величину постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянном процентной ставке.

Синтаксис: ПЛТ(ставка; кпер; пс; бс; тип).

Аргументы:

ставка—процентная ставка по ссуде, кпер — общее число выплат по ссуде, пс — приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой, бс — требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение бс равно 0, Тип — число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.

Если бс = 0 и тип = 0, то функция ПЛТ вычисляет по формуле 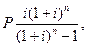(1):

(1)

где Р — пс;

i — ставка;

n — кпер.

Отметим, что очень важно быть последовательным в выборе единиц измерения для задания аргументов ставка и КПЕР. Например, если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12% годовых, то для задания аргумента ставка используйте 12%/12, а для задания аргумента КПЕР - 4*12. Если вы делаете ежегодные платежи по тому же займу, то для задания аргумента ставка используйте 12%, а для задания аргумента КПЕР - 4.

Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на величину КПЕР. Интервал выплат — это последовательность постоянных денежных платежей, осуществляемых за непрерывный период. Например, заем под автомобиль или заклад являются интервалами выплат. В функциях, связанных с интервалами выплат, выплачиваемые вами деньги, такие как депозит на накопление, представляются отрицательным числом, а деньги, которые вы получаете, такие как чеки на дивиденды, представляются положительным числом. Например, депозит в банк на сумму 1000 руб. представляется аргументом -1000, если вы вкладчик, и аргументом 1000, если вы — пpeдставитель банка.

Задание

Рассчитайте 5-летнюю ипотечную ссуду в размере 500 тыс. руб. со ставкой 18% годовых при начальном взносе 20% и ежемесячной (ежегодной) выплате.

Задание выполняйте в новой книге Задания.xls , Лист1 переименуйте в ПЛТ.

Порядок отчета лабораторной работы:

При отчете лабораторной работы необходимо:

1) Продемонстрировать выполненные упражнения, описанные в методических указаниях;

2) Продемонстрировать выполненное задание, прокомментировать порядок его выполнения и объяснить полученные результаты;

3) Ответить на контрольные вопросы.

Контрольные вопросы:

1) Какие задачи позволяет решать Microsoft Excel?

2) Как вызывается нужная функция?

3) Какие категории функций Вам известны?

4) Что позволяет вычислить функция ПЛТ?

5) Какие параметры у функции ПЛТ?

Список литературы:

1. Гарнаев А.Ю. Использование MS Excel и VBA в экономике и финансах.-СПб.: БХВ- Санкт-Петербург, 1999.- 336 с., ил.

2. Информатика. Серия «Учебники, учебные пособия». И57 // Под ред. П.П. Беленького. – Ростов н/Д: Феникс, 2002. 448с.

3. А.В. Могилев, Пак, Хеннер. Информатика. М: Изд. центр «Академия», 2000г.- 816 с.

Лабораторная работа №2