Расчет простых и сложных процентов.

Процент – сумма дохода от предоставления капитала в долг или плата за пользование ссудным капиталом во всех его формах (депозитный процент, кредитный процент, процент по облигациям, процент по векселям и т.п.).

Процентная ставка, используемая в процессе наращения или дисконтирования стоимости денежных средств (оценки их будущей и настоящей стоимости), классифицируется по следующим основным признакам.

1. По использованию в процессе форм оценки стоимости денег во времени:

а) ставка наращения – процентная ставка, по которой осуществляется процесс наращения стоимости денежных средств (компаундинг), т.е. определяется их будущая стоимость;

б) ставка дисконтирования (дисконтная ставка) – процентная ставка, по которой осуществляется процесс дисконтирования стоимости денежных средств, т.е. определяется их настоящая стоимость.

2. По стабильности уровня используемой процентной ставки в рамках периода начисления:

а) фиксированная ставка – ее уровень неизменен на протяжении всех интервалов общего периода начисления;

б) плавающая (или переменная) процентная ставка – по соглашению сторон ее уровень регулярно пересматривается в отдельных интервалах общего периода начислений.

3. По обеспечению начисления определенной годовой суммы процента:

а) периодическая ставка процента – при обеспечении определенной годовой суммы процента может варьировать как по уровню, так и по продолжительности отдельных интервалов на протяжении годового периода платежей;

б) эффективная ставка процента (или ставка сравнения) – характеризует среднегодовой уровень ставки, определяемый отношением годовой суммы процента, начисленного по периодическим его ставкам, к основной сумме капитала.

4. По условиям формирования:

а) базовая процентная ставка – характеризуется определенным исходным ее уровнем в качестве первоначальной основы последующей ее конкретизации кредитором (заемщиком) в зависимости от условий осуществления соответствующей инвестиционной операции;

б) договорная процентная ставка – характеризует конкретизированный ее уровень, согласованный кредитором и заемщиком и отраженный в соответствующем инвестиционном договоре.

Методика оценки стоимости денег по простым процентам.

1. При расчете суммы простого процента в процессе наращения стоимости (компаундинга) используется следующая формула:

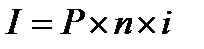
I – сумма процента за обусловленный период времени в целом;

P – первоначальная сумма (стоимость) денежных средств;

n – количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени;

i – используемая процентная ставка, выраженная десятичной дробью.

Будущая стоимость вклада с учетом начисленной суммы процента определяется по формуле:

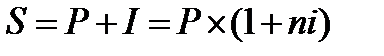
Множитель (1+ni) называется множителем (или коэффициентом) наращения суммы простых процентов. Его значение всегда должно быть больше единицы.

2. При расчете суммы простого процента в процессе дисконтирования стоимости (т.е. суммы дисконта) используется следующая формула:

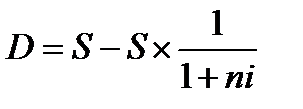
D – сумма дисконта (рассчитанная по простым процентам) за обусловленный период времени в целом;

S – стоимость денежных средств;

n – количество интервалов, по которым осуществляется расчет процентных платежей, в общем обусловленном периоде времени;

i – используемая дисконтная ставка, выраженная десятичной дробью.

Настоящая стоимость денежных средств (Р) с учетом рассчитанной суммы дисконта определяется по формуле:

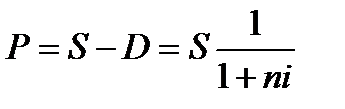
Множитель ( 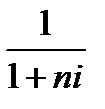) называется дисконтным множителем (коэффициентом) суммы простых процентов, значение которого всегда должно быть меньше единицы.

Методика оценки стоимости денег по сложным процентам.

1. При расчете будущей суммы вклада (стоимости денежных средств) в процессе его наращения по сложным процентам используется следующая формула:

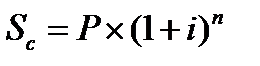
S_c – будущая стоимость вклада (денежных средств) при его наращении по сложным процентам;

P – первоначальная сумма вклада;

i – используемая процентная ставка, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

Сумма процента (I_c) в этом случае определяется по формуле:

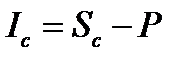
2. При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам используется следующая формула:

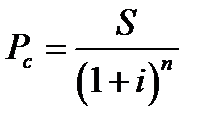
P_c – первоначальная сумма вклада;

S – будущая стоимость вклада при его наращении, обусловленная условиями инвестирования;

i – используемая дисконтная ставка, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периоде времени.

Сумма дисконта (D_c) в этом случае определяетсяпо формуле

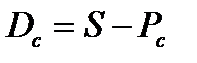
3. При определении средней процентной ставки, используемой в расчетах стоимости денежных средств по сложным процентам, применяется следующая формула:

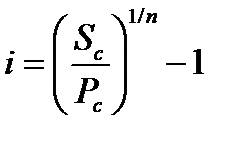
i – средняя процентная ставка, используемая в расчетах стоимости денежных средств по сложным процентам, выраженная десятичной дробью;

S_c – будущая стоимость денежных средств;

P_c – настоящая стоимость денежных средств;

n – количество интервалов, по которым осуществляется каждый процентный платеж, в общем обусловленном периодевремени.

4. Длительность общего периода платежей, выраженная количеством его интервалов, в расчетах стоимости денежных средств по сложным процентам определяется путем логарифмирования по следующей формуле:

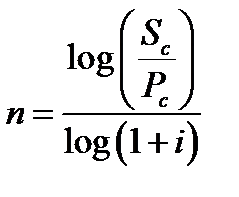
S_c – будущая стоимость денежных средств;

P_c – настоящая стоимость денежных средств;

i – используемая процентная ставка, выраженная десятичнойдробью.

5. Определение эффективной процентной ставки в процессе наращения стоимости денежных средств по сложным процентам осуществляется по формуле:

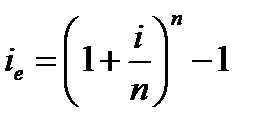
i_е – эффективная среднегодовая процентная ставка при наращении стоимости денежных средств по сложным процентам, выраженная десятичной дробью;

i – периодическая процентная ставка, используемая при наращении стоимости денежных средств по сложным процентам, выраженная десятичной дробью;

n – количество интервалов, по которым осуществляется каждый процентный платеж по периодической процентной ставке на протяжении года.

При оценке стоимости денег во времени по сложным процентам необходимо иметь в виду, что на результат оценки оказывает большое влияние не только используемая ставка процента, но и число интервалов выплат в течение одного и того же общего платежного периода. Иногда оказывается более выгодным инвестировать деньги под меньшую ставку процента, но с большим числом интервалов в течение предусмотренного периода платежа.

Множители (1+i)ⁿ и 1/(1+i)ⁿ называются соответственно множителем наращения и множителем дисконтирования суммы сложных процентов.