Тема 1.2. Финансовые вычисления
Тесты
1. Банковский вклад за один и тот же период увеличивается больше при применении ... процентов
А) простых
Б) сложных
2. Годовая номинальная ставка банковского процента ... годовой фактической ставки:
А) больше
Б) меньше
В) равна
3. Метод аннуитета применяется при расчете:
А) равных сумм платежей через равные промежутки времени
Б) остатка долга по кредиту
В) величины процентов на вклады
4. Дисконтирование - это ...
А) определение будущей стоимости сегодняшних денег
Б) определение текущей стоимости будущих денежных средств
В) учет инфляции
5. Термин «альтернативные издержки» или «упущенная выгода» означает
А) уровень банковского процента
Б) доход, от которого отказывается инвестор, вкладывая деньги в иной
проект
В) издержки по привлечению данной суммы денежных средств
Г) доходность государственных ценных бумаг
6. При использовании долгосрочного кредита расчет ежегодных общих сумм платежей методом аннуитета ... общие выплаты по кредиту
А) уменьшает
Б) увеличивает
В) не изменяет
7. Метод ежегодного погашения кредита равными суммами и метод аннуитета при погашении кредита и выплате процентов приводит к существенной разнице ежегодных выплат при:
А) высокой ставке процентов за кредит
Б) небольшой сумме кредита
В) коротких сроках его погашения
8. По какой формуле рассчитывается процентная ставка, если известно, что PV - исходная сумма, FV - сумма, ожидаемая к поступлению?
А) 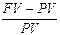 Б)
Б) 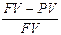 В)
В) 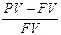
9. В чём состоит принципиальная разница между простым и сложным
процентом?
А) ни в чём
Б) начисление простых процентов происходит с неизменной базы, а сложных - с постоянно возрастающей
В) начисление сложных процентов происходит с неизменной базы, а простых - с постоянно возрастающей
10. При каких условиях будущая и дисконтированная стоимости совпадают?
А) при коэффициенте дисконтирования, равным 1
Б) при дефляции или отсутствии инфляции в экономике страны
В) при коэффициенте дисконтирования равным 0
11. Какая схема наиболее удобна (приемлема) при начислении процентов за дробное число лет?
А) смешанная схема, предусматривающая начисление сложных процентов за целое число лет и простых процентов за дробную часть года
Б) схема сложных процентов
В) схема простых процентов
12. Что такое аннуитет пренумерандо?
А) денежный поток с равными поступлениями, осуществляющимися в начале периода
Б) денежный поток с равными поступлениями, осуществляющимися неопределённо долго
В) денежный поток с равными поступлениями, осуществляющимися в начале периода и продолжающийся ограниченное время
13. Указать название ставки, по которой за базу начисления процентов берётся первоначальная сумма долга.
А) антисипативная
Б) учётная
В) декурсивная
14. Какой тип наращения предпочтителен при хранении денег в банке?
А) простые проценты
Б) зависит от процентной ставки
В) сложные проценты
15. На счете в банке 1,1 млн. руб. Банк платит 20% годовых. Предлагается войти всем капиталом в совместное предприятие, при этом прогнозируется удвоение капитала через 5 лет. Каким образом следует поступить?
А) принять решение
Б) не принимать
16. Инвестор имеет 10 млн. руб. и хотел бы удвоить эту сумму через 3 года.
Каково минимально приемлемое значение процентной ставки?
А) 33,3%
Б) 20,5%
В) 26%
17. Банк предлагает 10% годовых.
Чему должен быть равен первоначальный вклад, чтобы через 3 года иметь на счете 10 млн. руб.?
А) 3,3 млн. руб.
Б) 8 млн. руб.
В) 2,7 млн. руб.
18. Какая сумма предпочтительнее при ставке 10% - 1300 млн. руб. сегодня
или 2600 млн. руб. через 5 лет?
А) 1300 млн. руб.
Б) 2600 млн. руб.
В) нет правильных ответов
19. Рассчитайте наращенную сумму с исходной суммы 2 млн. руб. при размещении ее в банк
под 10% годовых на 5 лет по сложной ставке процентов.
А) 3,0 млн. руб.
Б) 2,2 млн. руб.
В) нет правильных ответов
20. На вклад в банк в размере 2 млн. руб. сроком на 3 года банк начисляет 10% годовых. Какая сумма будет на счете к концу срока, если начисление процентов производится по схеме сложных процентов каждые полгода?
А) 2,7 млн. руб.
Б) 3,2 млн. руб.
В) 1,6 млн. руб.
21. Клиент занял на 4 года 9 млн. руб. под 10% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определите величину годового платежа.
А) 2,8 млн. руб.
Б) 3,2 млн. руб.
В) 1,8 млн. руб.
22. Инвестор вложил 8000 тыс. руб. в пенсионный контракт. На основе анализа таблиц смертности страховая компания предложила условия, согласно которым определенная сумма будет выплачиваться ежегодно в течение 10 лет исходя из ставки 16 % годовых. Какую сумму будет получать ежегодно инвестор?
А) 1264,5 тыс. руб.
Б) 1384,6 тыс. руб.
В) 1655,2 тыс. руб.
23. К моменту выхода на пенсию, т.е. через 8 лет, инвестор желает иметь на счету 30 млн. руб. Для этого он намерен делать ежегодный взнос в банк по схеме пренумерандо. Определить размер взноса, если банк предлагает 8 % годовых.
А) 3,2 млн. руб.
Б) 2,6 млн. руб.
В) 1,6 тыс. руб.
24. Рассчитайте будущую стоимость 10 млн. руб. через 5 лет, если банк начисляет проценты 3 раза в год по ставке 8% годовых.
А) 29,7 млн. руб.
Б) 24,8 млн. руб.
В) 36,6 тыс. руб.
25. Рассчитайте текущую стоимость денежного поступления в 30 млн. руб. через 7 лет, если коэффициент дисконтирования равен 13 % годовых.
А) 13,2 млн. руб.
Б) 12,8 млн. руб.
В) 11,6 тыс. руб.
26. Какие условия предоставления кредита более выгодны банку:
А) 27% годовых, начисление ежеквартальное;
Б) 29% годовых, начисление полугодовое?
27. Предприятие приобрело здание за 20 млн. руб. на следующих условиях:
1) 25% стоимости оплачивается немедленно;
2) оставшаяся часть оплачивается равными годовыми платежами в течение 10 лет с начислением 13 % годовых на непогашенную часть кредита по схеме сложных процентов. Определите величину годового платежа.
А) 2,8 млн. руб.
Б) 3,2 млн. руб.
В) 1,6 тыс. руб.
28. Банк А начисляет доход по сложному проценту раз в полгода из расчёта 20% годовых, банк Б – по простому проценту. Сумма вклада 10000 тыс. руб. Какой процент должен начислять банк Б, чтобы по итогам трёх лет клиент получил сумму на 10% больше, чем в банке А?
А) 29,5%
Б) 30,3%
В) 31,6%
29. Инвестор вносит в банк по 10 тыс. руб. в конце каждого квартала. Банк начисляет по 5% в квартал по сложной ставке. Какая сумма будет на счёте через год?
А) 42 тыс. руб.
Б) 43,1 тыс. руб.
В) 44, 2 тыс. руб.
30. Банк А начисляет 0,4% в месяц, банк Б начисляет 2,5% раз в полгода. С учётом реинвестирования куда выгоднее вкладывать: в А или Б?
А) А лучше Б
Б) Б лучше А
В) одинаковые условия
31. Инвестор имеет 100 тыс. руб. в начале 2013 г. Он хочет разместить их так, чтобы в начале 2018 г. у него было не менее 300 тыс. руб. Банк А предлагает исчисление 10% на сумму, находящуюся на счёте, один раз в полгода. Банк Б предлагает начисление 25% на сумму находящуюся на счёте один раз в год. В какой из банков следует вложить деньги при прочих равных условиях?
А) банк А
Б) банк Б
В) ни в какой, т.к. ни один банк не выполняет этих требований
Задания
1. а) Первоначальная сумма Р руб. помещена в банк на срок п лет под i% годовых (проценты простые). Определить наращенную сумму, эквивалентные значения простой учетной ставки, сложной процентной ставки, сложной номинальной процентной ставки (проценты начисляются т раз в году). Найти наращенную сумму, если ставка налога на проценты q%. Уровень инфляции за рассматриваемый период оказался равным α%. Какова реальная доходность операции?
б) Первоначальная сумма Р руб., наращенная сумма S руб., процентная ставка i % годовых (проценты простые). Определить период начисления.
в) Первоначальная сумма Р руб., наращенная сумма S руб., период начисления п лет. Определить простую процентную ставку.
г) Первоначальная сумма Р руб. помещена в банк на срок с а по b под i% годовых (проценты простые). Определить наращенную сумму при К=365 дней.
| Вариант | Р | n | i | q | т | α | S | а | b |
| 0,5 | 1,1 | 12.03 | 27.08 | ||||||
| 0,25 | 1,2 | 03.04 | 15.09 | ||||||
| 0,75 | 1,3 | 11.05 | 09.10 | ||||||
| 0,5 | 1,4 | 17.06 | 23.11 | ||||||
| 0,25 | 1,5 | 24.07 | 05.12 | ||||||
| 0,75 | 1,6 | 23.03 | 14.08 | ||||||
| 0,5 | 1,7 | 16.04 | 26.09 | ||||||
| 0,25 | 1,8 | 19.05 | 21.10 | ||||||
| 0,75 | 1,9 | 24.06 | 09.11 | ||||||
| 0,75 | 11.07 | 15.12 |
Методические указания к решению задания 1
Пусть Р ‒ первоначальная сумма, S ‒ наращенная сумма, i ‒ годовая процентная ставка (проценты простые). Так как проценты простые, то в течение всего периода начисления они применяются к первоначальной сумме Р. Если п ‒ период начисления процентов (в годах), то наращенная сумма через п лет S = Р (1 + ni).
Зная первоначальную сумму Р, наращенную сумму S, простую годовую процентную ставку i, можно определить период начисления n (в годах): S = Р (1 + ni) => 1 + ni = S/Р => ni = S/Р ‒ 1 => n = 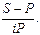
Зная первоначальную сумму Р, наращенную сумму S, период начисления n (в годах), можно определить простую годовую процентную ставку S = Р (1+ni)=>1+ni = S/ P=>ni = S/ P‒1=>i= 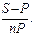
Математическим дисконтированием называется операция, когда по наращенной сумме S, периоду начисления n и простой процентной ставке i нужно определить первоначальную сумму Р:S=Р(1+ni)=> P=S/(1+ni).
В формуле S = Р (1+ ni) период начисления п измеряется в годах. Это не всегда удобно, так как период начисления может быть меньше года (например, с 18 марта 2014 года по 20 октября 2014 года). В этом случае полагают n ‒ t/K, где t ‒ период начисления (в днях), К ‒ продолжительность года (в днях). Тогда S=Р(1+it/К). Дата выдачи и дата погашения ссуды всегда считаются за один день.
2.а) Первоначальная сумма Р руб. помещена в банк на срок п лет под простую учетную ставку d% годовых. Определить наращенную сумму, эквивалентные значения простой процентной ставки, сложной процентной ставки, сложной номинальной процентной ставки (проценты начисляются т раз в году). Найти наращенную сумму, если ставка налога на проценты q%. Уровень инфляции за рассматриваемый период оказался равным α%. Какова реальная доходность операции?
б) Первоначальная сумма Р руб., наращенная сумма S руб., простая учетная ставка d% годовых. Определить период начисления.
в) Первоначальная сумма Р руб., наращенная сумма S руб., период начисления п лет. Определить простую учетную ставку.
г) Первоначальная сумма Р руб. помещена в банк на срок с a nob под простую учетную ставку d% годовых. Определить наращенную сумму при К=365 дней.
| Вариант | Р | п | d | т | α | S | а | b | q |
| 0,5 | 1,1 | 12.03 | 27.08 | ||||||
| 0,25 | 1,2 | 03.04 | 15.09 | ||||||
| 0,75 | 1,3 | 11.05 | 09.10 | ||||||
| 0,5 | 1,4 | 17.06 | 23.11 | ||||||
| 0,25 | 1,5 | 24.07 | 05.12 | ||||||
| 0,75 | 1,6 | 23.03 | 14.08 | ||||||
| 0,5 | 1,7 | 16.04 | 26.09 | ||||||
| 0,25 | 1,8 | 19.05 | 21.10 | ||||||
| 0,75 | 1,9 | 24.06 | 09.11 | ||||||
| 0,75 | 11.07 | 15.12 |
Методические указания к решению задания 2
В задании используется антисипативный способ начисления простых процентов. Сумма получаемого дохода рассчитывается, исходя из наращенной суммы S. S ‒ это величина получаемого кредита. Заемщик получает в начале периода начисления процентов сумму Р = S ‒ Д где D ‒ это дисконт (разность между размером кредита S и непосредственно выданной суммой Р). Такая операция называется дисконтированием по простой учетной ставке (банковским учетом). Пусть d ‒ простая учетная ставка, п ‒ период начисления процентов (в годах). Тогда D = ndS и Р= S ‒ D = S‒ndS = S(1 ‒ nd). На практике простые учетные ставки применяются при учете (покупке) векселей.
3.а) Первоначальная сумма Р руб. помещена в банк на срок п лет под i % годовых (проценты сложные). Определить наращенную сумму, эквивалентные значения простой учетной ставки, простой процентной ставки, сложной номинальной процентной ставки (проценты начисляются т раз в году). Уровень инфляции за рассматриваемый период оказался равным α%. Какова реальная доходность операции?
б) Первоначальная сумма Р руб., наращенная сумма S руб., процентная ставка i% годовых (проценты сложные). Определить период начисления.
в) Первоначальная сумма Р руб., наращенная сумма S руб., период начисления п лет. Определить сложную процентную ставку.
| Вариант | Р | п | i | т | α | S |
| 1,1 | ||||||
| 1,2 | ||||||
| 1,3 | ||||||
| 1,4 | ||||||
| 1,5 | ||||||
| 1,6 | ||||||
| 1,7 | ||||||
| 1,8 | ||||||
| 1,9 | ||||||
Методические указания к решению задания 3
Пусть Р ‒ первоначальная сумма, S ‒ наращенная сумма, i ‒ годовая процентная ставка (проценты сложные). Так как проценты сложные, то в конце каждого интервала начисления процентная ставка применяется к наращенной сумме на начало этого интервала начисления. Если п‒ период начисления процентов (в годах), то наращенная сумма через плет S = Р(1 + i)n.
При использовании простой процентной ставки i наращенная сумма равна S1 = Р(1+ni). При использовании сложной процентной ставки iсл наращенная сумма будет S2 = Р(1 + iсл )n .
Так как ставки эквивалентны, то наращенные суммы равны: S1 = S2, то есть Р(1 + ni) = Р(1 + iсл )n . Отсюда 1 + ni = Р(1 + iсл )n => i = ((1 + iсл)n -1)/n.
При использовании номинальной сложной процентной ставки j (проценты за год начисляются т раз) наращенная сумма будет S2 = Р(1 +j/т)пт.
Так как ставки эквивалентны, то наращенные суммы равны: S1=S2,то есть P(1+iсл)n = Р(1+j/т)пт. Отсюда 1+iсл=(1+j/т)т => iсл=(1+j/m)m ‒1. Эта формула определяет эффективную годовую ставку сложных процентов, эквивалентную номинальной сложной процентной ставке, и не зависит от периода начисления п.
Cумму Sα можно получить, поместив первоначальную сумму Р на срок п под сложную ставку ссудных процентов iα, учитывающую инфляцию: Sα = Р (1+iα)n.
Отсюда Р(1+i)n (1+ α) = Р(1+iα) п =>(1+i)n (1+α) = (1+ia)n => (1+ia)n =>(1+i) 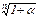 =1+iα=>iα=(1+i)
=1+iα=>iα=(1+i) 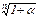 ‒1. Именно под такую сложную ставку ссудных процентов нужно положить первоначальную сумму на срок п, чтобы при уровне инфляции а за рассматриваемый период обеспечить реальную доходность в виде сложной годовой ставки ссудных процентов /.
‒1. Именно под такую сложную ставку ссудных процентов нужно положить первоначальную сумму на срок п, чтобы при уровне инфляции а за рассматриваемый период обеспечить реальную доходность в виде сложной годовой ставки ссудных процентов /.
(1+i) 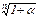 =1+iα=>i=(1+ia)/
=1+iα=>i=(1+ia)/ 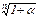 ‒1. Это формула реальной доходности в виде сложной годовой ставки ссудных процентов для случая, когда первоначальная сумма была инвестирована под сложную ставку ссудных процентов iα на срок п при уровне инфляции α за рассматриваемый период.
‒1. Это формула реальной доходности в виде сложной годовой ставки ссудных процентов для случая, когда первоначальная сумма была инвестирована под сложную ставку ссудных процентов iα на срок п при уровне инфляции α за рассматриваемый период.
4.а) Размер ежегодных платежей R руб., срок п лет, проценты начисляются по сложной процентной ставке i% годовых. Определить наращенную (будущую) сумму и современную стоимость простых рент постнумерандо и пренумерандо. Преобразовать эту простую ренту в общую ренту (проценты начисляются т раз в году, р платежей в году).
б) Определить размер ежегодных платежей в конце года по сложной процентной ставке i% годовых для накопления через п лет суммы S руб.
в) Определить размер ежегодных платежей в конце года по сложной процентной ставке i% годовых для погашения в течение п лет долга A руб.
г) Размер ежегодных платежей R руб., процентная ставка i% годовых, наращенная сумма S руб. Определить сроки простых рент постнумерандо и пренумерандо.
д) Размер ежегодных платежей R руб., процентная ставка i% годовых, современная стоимость А руб. Определить сроки простых рент постнумерандо и пренумерандо.
е) Определить, под какую процентную ставку нужно вносить каждый год R руб., чтобы через п лет накопить сумму S руб. (для рент постнумерандо и пренумерандо).
ж) Определить, под какую процентную ставку нужно вносить каждый год R руб., чтобы через п лет погасить долг А руб. (для рент постнумерандо и пренумерандо).
з) Современная стоимость бессрочной ренты постнумерандо А руб., процентная ставка i% годовых. Определить размер ежегодных выплат.
| Вариант | R | п | i | S | А | t | W | т | Р |
Методические указания к решению задания 4
Наращенная (будущая) сумма для простой ренты:
1) постнумерандо определяется по формуле S=R(1+i)n-1+ +R (1+i)n-2 + R (1+i)n-3 + ... + R (1+i)+ R= R 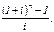
2) пренумерандо определяется по формуле S=R(1+i)n+R (1+ i)n-1 + +R (1+i)n-2 + R (1+i)2 + ... + R (1+i)= R (1+i) 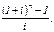
Современная стоимость для простой ренты:
3) постнумерандо определяется по формуле A=R/(1+i)+ +R/(1+i)2 + R/(1+i)3 + ... + R/(1+i)n-1 +R/(1+i)n=R 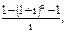
4) пренумерандо определяется по формуле A=R+R/(1+i) + R/(1+i)2 + ... + R/(1+i)n +R/(1+i)n-1=R(1+i) 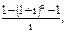
5) Преобразование простой ренты в общую осуществляется по формуле W= R ((1+i)m/p ‒1)/i, где W и R – величины выплат общей и простой рент соответственно.
6) Современная стоимость бессрочной ренты постнумерандо определяется из соотношения А=R/i
5.Банк выдает кредит на сумму А, срок п лет, процентная ставка i% годовых. Составить план погашения долга c помощью простой ренты постнумерандо на основе приведённой таблицы.
| Год | Остаток непогашенного долга на конец года | Годовой взнос | ||
| Сумма погашения основного долга | Сумма погашения процентов | Всего | ||
| … | ||||
| n |
Методические указания к решению задания 5
Для определения погасительного взноса следует воспользоваться выражением R=Ai/(1-1/(1+i)n)
МОДУЛЬ 2 АНАЛИЗ И ПЛАНИРОВАНИЕ В УПРАВЛЕНИИ
ФИНАНСАМИ ПРЕДПРИЯТИЯ
