Оценка инструментов с фиксированными доходами на основании расчета приведенной стоимости
В главе 4 описано, что если существует единственная безрисковая (ее также называют гарантированной, или надежной) процентная ставка, расчет приведенной стоимости любого потока ожидаемых денежных поступлений не представляет особой сложности. Эта задача включает в себя применение формулы расчета чистой приведенной стоимости с использованием безрисковой процентной ставки в качестве ставки дисконтирования.
Предположим, что вы приобрели ценную бумагу с фиксированным доходом с ежегодной выплатой по ней 100 долл. на протяжении последующих трех лет. Какова стоимость этого трехлетнего финансового контракта типа аннуитета, если известно, что соответствующая дисконтная ставка составляет 6% в год? Как показано в главе 4, ответ будет равен 267,30 долл. и может быть легко получен с помощью специального финансового калькулятора, таблицы, в которой указаны коэффициенты приведенной стоимости или с помощью математической формулы.
Напомним формулу для расчета приведенной стоимости обычного аннуитета, равного 1 долл. для периодов, при процентной ставке (i):
| PV = | 1 - (1+i)-n |
| i |
В финансовый калькулятор введем значения для и, (", РМТ и рассчитаем приведенную стоимость (PV):
| n | i | PV | FV | РМТ | Результат |
| ? | Pl/=267,30 |
Теперь предположим, что через час после покупки этой ценной бумаги вам необходимо ее продать, но за это время безрисковая процентная ставка поднялась с 6% до %в год. Сколько теперь можно получить за нее?
Уровень процентных ставок изменился, но ожидаемые денежные поступления от инвестиций в данную ценную бумагу остались неизменными. Для того чтобы инвестор смог получить 7% доходности в год, цена этого актива должна понизиться. Насколько? До той отметки, при которой она будет равна приведенной стоимости ожидаемых денежных потоков, дисконтированных по 7%-ной ставке.
| n | i | PV | FV | PMT | Результат |
| ? | PV=262,43 |
Ценная бумага с фиксированным доходом с ежегодной выплатой по ней 100 долл. на протяжении последующих трех лет имеет приведенную стоимость 262,43 долл. и обеспечивает своему владельцу доходность в размере 7% в год. Таким образом, при повышении рыночных процентных ставок курс любых ценных бумаг с фиксированным доходом понижается. Это связано с тем, что инвесторы приобретут только в том случае, если они обеспечат им уровень доходности, соответствующий новым рыночным условиям.
Итак, повышение процентной ставки на 1% приведет к падению курса ценной бумаги на 4,87 долл. И наоборот, понижение процентной ставки приведет к соответствующему повышению ее курса.
Это иллюстрирует основной принцип, используемый при оценке активов с заведомо известными, фиксированными денежными потоками. Изменение рыночных процентных ставок приводит к изменению в противоположном направлении рыночных цен всех имеющихся финансовых контрактов с фиксированными поступлениями платежей.
Поскольку процесс изменения процентных ставок непредсказуем, то и курс ценных бумаг с фиксированным доходом непредсказуем вплоть до момента их погашения.
| Контрольный вопрос 8.1 |
| Что произойдет с курсом ценной бумаги с фиксированным доходом с ежегодной выплатой по ней 100 долл., если рыночная процентная ставка упадет с 6% до 5% годовых? |
На практике оценка стоимости известных денежных потоков не всегда так проста, как в приведенном примере. Это связано с тем, что в реальной жизни обычно неизвестно, какую именно дисконтную ставку следует использовать в формуле вычисления, приведенной стоимости денежных поступлений. Как было отмечено в главе 2, рыночные процентные ставки различаются в зависимости от сроков погашения финансовых инструментов. На рис. 8.1 представлен график, отображающий кривую доходности (зависимость между доходностью облигаций примерно одинакового инвестиционного качества и сроками их погашения. — Прим. ред.) по облигациям Казначейства США.
Было бы заманчиво предположить, что для оценки трехлетнего аннуитета, рассматриваемого в нашем примере, в качестве дисконтной ставки может быть применена процентная ставка по облигациям Казначейства США со сроком погашения 3 года. Однако это было бы неправильно. Реальная процедура, позволяющая выполнять оценку других известных денежных потоков на основании информации, содержащейся в кривой доходности, намного более сложна.
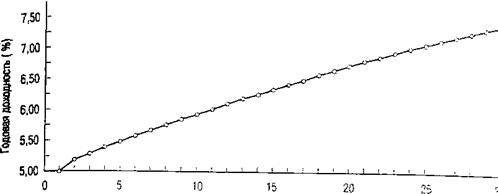
Срок до погашения (лет) Источник. The Wall Street Journal, April 3, p.C21
Рис. 8.1. Кривая доходности ценных бумаг Казначейства США
