МОДЕЛЬ совершенной конкуренции.

Все товары отрасли являются совершенными заменителями, а перекрестная эластичность спроса по цене для любой пары фирм стремится к бесконечности:

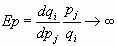
Это означает, что любое сколь угодно малое повышение цены одним производителем сверх рыночного уровня ведет к сокращению спроса на его продукцию до нуля. Неценовая конкуренция отсутствует.

Количество экономических субъектов на рынке неограниченно велико, а их удельный вес столь мал, что решения отдельной фирмы (отдельного потребителя) об изменении объема ее продаж (покупок) не влияют на рыночную ценупродукта. При этом, естественно, предполагается отсутствие сговора между продавцами или покупателями для получения монопольной власти на рынке. Рыночная цена является результатом совместных действий всех покупателей и продавцов.

14. Дискретные зависимые переменные и цензурированные выборки: модели бинарного и множественного выбора, модели с урезанными и цензурированными выборками

В классических моделях линейной регрессии относительно зависимой переменной явно или неявно предполагалось, что она выражает количественный признак, принимая «непрерывное» множество значений. В частности, в нормальной линейной регрессионной модели предполагается, что ошибка имеет гауссовское распределение, откуда следует, что зависимая переменная у может принимать любые значения. В то же время довольно часто интересующая нас величина по своей природе является дискретной. Выделим несколько типичных ситуаций.

1. Выбор из двух или нескольких альтернатив. Примеры:

· голосование;

· решение работать или не работать;

· решение покупать или не покупать какой-либо товар длительного пользования (автомобиль, дом и т.п.);

· форма собственности (государственная, смешанная, частная);

· выбор профессии (научный работник, преподаватель, консультант, менеджер);

· способ попадания из дома на работу (пешком, автобус, метро, метро и автобус, автомобиль); и т.д.

Если есть только две возможности (бинарный выбор), то результат наблюдения обычно описывается переменной, принимающей значения 0 или 1, называемой бинарной. В общем случае при наличии k альтернатив результат выбора можно представить переменной, принимающей, например, значения l,...,k. Если альтернативы нельзя естественным образом упорядочить (как в двух последних примерах), то их нумерация может быть произвольной. В этих случаях соответствующую переменную называют номинальной (qualitative).

· 2.Ранжированный выбор. Как и в первом случае, есть несколько альтернатив, но они некоторым образом упорядочены. Примеры:

· доход семьи (низкий, средний, высокий, очень высокий);

· уровень образования (незаконченное среднее, среднее, среднее техническое, высшее);

· состояние больного (плохое, удовлетворительное, хорошее); И т.д.

Соответствующая переменная называется порядковой, ординальной или ранговой (ranking).

3.Количественная целочисленная характеристика. Примеры:

· количество прибыльных предприятий;

· количество частных университетов;

· число патентов, зарегистрированных в течение года; и т. д.

Для моделей с дискретными зависимыми переменными конечно же возможно формальное применение метода наименьших квадратов, однако достаточно удовлетворительные с содержательной точки зрения результаты можно при этом получить, как правило, лишь для моделей третьей группы с количественными целочисленными переменными. В случае порядковых переменных интерпретация оценок коэффициентов при объясняющих переменных значительно затруднена: увеличение на единицу порядковой переменной означает переход к следующей по рангу альтернативе, однако далеко не всегда переход от первой альтернативы ко второй численно эквивалентен переходу от второй к третьей.

Если же зависимая переменная является номинальной и количество альтернатив больше двух, то результаты оценивания вообще теряют смысл в силу произвольности нумерации альтернатив. Таким образом, стандартная регрессионная схема, которую мы использовали ранее для анализа зависимости интересующей нас переменной от экзогенных факторов, в случае номинальных эндогенных переменных нуждается в существенной коррекции.

Сначала рассматриваются модели бинарного выбора, затем показывается, что модели с несколькими альтернативами могут быть либо непосредственно сведены к моделям бинарного выбора, либо могут быть исследованы аналогичными методами.

Другой класс моделей, связан с цензурированными (censored) и урезанными (truncated) выборками. Классический пример цензурирования дает изучение расходов семей на покупку товаров длительного пользования (автомобиля, дома и т. п.). Ясно, что эти расходы не могут быть отрицательными и в то же время при проведении обследования будут встречаться наблюдения с нулевым значением этих расходов, что просто означает отказ от покупки соответствующего товара. Здесь осуществляется цензурирование выборки на уровне 0 значения зависимой переменной. Другой пример дает определение «времени жизни» технического изделия с помощью испытания в одинаковых условиях в течение определенного периода нескольких экземпляров изделия. Для тех образцов, которые в процессе испытаний вышли из строя, время жизни будет зафиксировано точно, для остальных временем жизни будет считаться длительность испытаний, а истинное его значение останется неизвестным. В этом случае уровнем цензурирования является период испытаний. Можно показать, что в подобных ситуациях непосредственное применение метода наименьших квадратов дает смещенные оценки параметров.

Пример урезания выборки дает исследование распределения семей по объему выплачиваемых налогов или изучение зависимости выплачиваемых налогов от размера семьи, возраста ее членов и т. п. Здесь из рассмотрения могут исключаться семьи, имеющие доход ниже официального уровня бедности. В этом случае уровень бедности определяет урезание выборки. Метод наименьших квадратов здесь также приводит к смещенным оценкам.

Разница между цензурированием и урезанием. В первой ситуации даже для цензурированного наблюдения известны значения независимых переменных, в то время как во втором случае известен лишь уровень урезания, а значения независимых переменных для исключенных из рассмотрения объектов неизвестны.

В случае бинарного выбора используются линейная модель вероятности, probitи logitмодели. Множественный выбор может быть представлен как последовательность бинарных выборов. Для цензурированных выборок используется tobitмодель, а также модели «времени жизни».

Модели «времени жизни»

Цензурирование или урезание наблюдений естественным образом возникает при исследовании длительности какого-либо процесса, времени нахождения в каком-либо состоянии: период безотказной работы прибора, время жизни пациента после трансплантации сердца, промежуток времени между двумя арестами рецидивиста, период безработицы, длительность забастовки и т. п. Модели подобных явлений называют моделями «времени жизни» (duration models). Если к моменту наблюдения процесс не завершился, то точное значение его длительности неизвестно и она цензурируется моментом наблюдения или же это наблюдение исключается из рассмотрения (урезание).

Модели «времени жизни» уже в течение нескольких десятилетий изучаются в технике, медицине, демографии. В экономике их исследование началось сравнительно недавно ((Lancaster, 1974), (Lancaster, 1985), (Heckman and Singer, 1984), (Kiefer, 1988)).

15. Панельные данные – основные модели: модель с фиксированным эффектом, модель со случайным эффектом

Панельные данные состоят из наблюдений одних и тех же экономических единиц, которые осуществляются в последовательные периоды времени. Панельные данные насчитывают три измерения: признаки (переменные) – объекты – время. Для них разработаны специальные методы анализа.

Имеется множество объектов (индивидуумы, домашние хозяйства, фирмы, регионы, страны и т.п.), занумерованных индексами 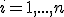. Они наблюдаются в моменты времени 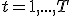. Каждый рассматриваемый объект характеризуется 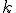переменными (признаками):

.

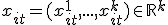Для большинства баз панельных данных характерно, что они содержат наблюдения о большом количестве объектов за относительно короткий промежуток времени.

Панельные данные ценны для экономистов тем, что при правильном их анализе можно избавиться от влияния индивидуальных особенностей объектов (individual heterogeneity), которые, как правило, являются одной из серьезнейших проблем анализа однократных данных.

Примеры использования моделей панельных данных

Пример 1. Макроэкономика. Объекты – страны; 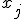– характеристики (например, инфляция, объем инвестиций, объем экспорта, импорта); 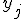– показатель ВВП на душу населения. Хотим выяснить, как он зависит от приведенных показателей.

Пример 2. Микроэкономика. Объекты – домашние хозяйства; 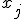– доход, число человек в семье, недвижимость, количество иждивенцев в семье, образование, возраст, пол; 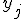– структура расходов. Данная задача часто возникает в маркетинге, когда необходимо выяснить каков рынок тех или иных товаров.

Пример 3. Объекты – выборка телезрителей ; 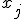– доход, образование, возраст, пол; 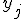– структура просмотров:

· часы – необходимо выяснить для каких групп населения выгодно проводить в данное время передачу или рекламу

· в каком отношении делятся по популярности передачи: развлечения/новости/спорт/…

· доля не попущения рекламы.

Пример 4. Объекты – коммерческие фирмы; 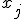– оборот, прибыль, число сотрудников, отрасль; 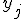– рыночная стоимость.

Обозначения

Введем обозначения:

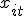· – набор независимых переменных (вектор размерности )

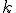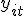· – зависимая переменная для экономической единицы 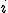в момент времени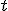

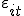· – соответствующая ошибка.

· Обозначим также:

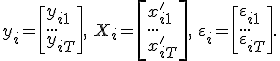
· Введем также «объединенные» наблюдения и ошибки:

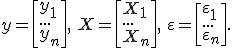
Здесь 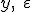– 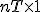векторы, 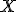– 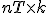матрица.