Условия правильности проведения выборочного отбора.

Основное условие – случайность отбора, репрезентативность или представительность отбора.

Ошибки репрезентативности могут быть систематическими и случайными. Случайные возникают в том случае, если выборочная совокупность недостаточно представительна. Систематические возникают при нарушении установленных правил отбора единиц.

Величина случайных ошибок определяет надежность данных выборочных наблюдений, их пригодность для суждения о генеральной совокупности. При помощи формул теории вероятности можно рассчитать возможную максимальную случайную ошибку – вероятностный (стохастический) предел ошибки выборки (Δ). Максимально возможная (предельная) ошибка – это отклонение выборочной средней (или доли) от генеральной средней (доли). Ее величина зависит:

– от степени колеблемости изучаемого признака генеральной совокупности

– от способа формирования выборочной совокупности

– от объема выборки.

Ошибка репрезентативности представляет собой разность между показателями выборочной и генеральной совокупности:

Для средней

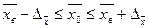
предельная ошибка выборки для средней

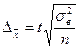[20] или 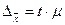, где

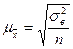– средняя ошибка выборки для средней

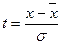– стандартное отклонение – «коэффициент доверия», который зависит от вероятности, с которой гарантируется предельная ошибка вероятности.

Для генеральной доли

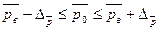
предельная ошибка выборки для доли

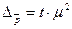[21], где

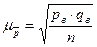[22] – средняя ошибка выборки для доли

Помимо ошибок репрезентативности существуют ошибки регистрации, которые свойственны для выборочного и сплошного наблюдения. Это ошибки, которые возникают вследствие недостаточной квалификации наблюдателя, неточности расчетов и несовершенством приборов.

Таким образом, ошибки статистического наблюдения складываются из ошибок регистрации (сплошное и выборочное наблюдение) и ошибок репрезентативности (выборочное наблюдение).

3. Задачи выборки:

– определение доверительных пределов, в которых находятся показатели генеральной совокупности (Δ)

– определение доверительной вероятности того, что разность между показателями выборочной и генеральной совокупности не превзойдет наперед заданного числа: Р = F(t). F(t) – интеграл вероятности.

– определение минимального объема выборки. Необходимо отобрать как можно меньше единиц выборки, но достаточное количество для данных условий (n)

Виды отбора:

– Повторный (по схеме возвращенного в урну шара)

– Бесповторный (по схеме не возвращенного в урну шара)

При повторном отборе численность единиц генеральной совокупности в процессе выборки остается неизменной. Ту или иную единицу, попавшую в выборку возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами попасть в выборку при повторном отборе.

При бесповторном отборе единица совокупности, попавшая в выборку не возвращается и при последующих отборах в выборке не участвует. Таким образом, при бесповторной выборке численности единиц генеральной совокупности сокращается в процессе исследования[23].

Способы отбора

Способы отбора определяют конкретный механизм отбора единиц из генеральной совокупности.

По степени охвата единиц совокупности разделяют большие и малые выборки (с объемом ).

Наибольшее распространение получили следующие виды выборки:

– собственно-случайная

– механическая

– типическая

– серийная (гнездовая)