Расчет индексов цен, физического объема и стоимости
| Вид товара | Единицы измерения | Цена за единицу, тыс. руб. | Количество реализованной продукции | Стоимость реализованной продукции, тыс. руб. | ||||
| I квартал | II квартал | I квартал | II квартал | I квартал | II квартал | Условная стоимость во 2-м квартале в ценах 1-го квартала | ||
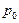 | 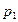 | 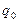 | 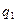 | 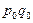 | 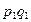 | 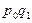 | ||
| А | Б | 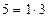 | 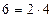 | 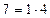 | ||||
| А | л | 1,0 | 1,5 | |||||
| Б | кг | 4,0 | 10,0 | |||||
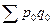 =2300 =2300 | 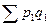 =5500 =5500 | 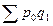 =3000 =3000 |
Решение: Прежде чем определить индексы, необходимо найти стоимость реализованной продукции за I-ый и II-ой кварталы, а также условную стоимость во II-м квартале при ценах I-го квартала (см гр.5, 6, 7 табл. 13).
А теперь построим индексную и факторную взаимосвязь и сделаем выводы:
Индексная связь
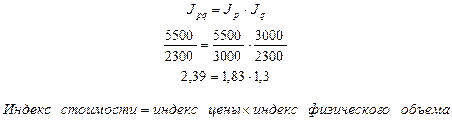
Фактическая взаимосвязь
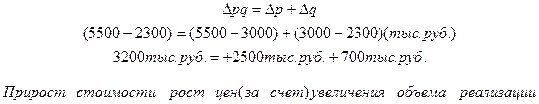
Таким образом, в отчетном периоде (II квартале) по сравнению с базисным (I квартал) стоимость реализованной продукции возросла на 139% ( 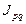 =2,39) за счет роста цен на 83% (
=2,39) за счет роста цен на 83% ( 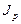 =1,83) и прироста объема реализованной продукции на 30% (
=1,83) и прироста объема реализованной продукции на 30% ( 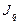 =1,3), что составило в абсолютном выражении прирост стоимости на 3200 тыс. руб., за счет роста цен прирост стоимости составил 2500 тыс. руб. и увеличилась стоимость реализованной продукции на 700 тыс. руб. за счет роста объема продукции; на сумму 2500 тыс. руб. произошел перерасход денежных средств у населения.
=1,3), что составило в абсолютном выражении прирост стоимости на 3200 тыс. руб., за счет роста цен прирост стоимости составил 2500 тыс. руб. и увеличилась стоимость реализованной продукции на 700 тыс. руб. за счет роста объема продукции; на сумму 2500 тыс. руб. произошел перерасход денежных средств у населения.
Надо отметить, что при построении индексов и изучении влияния изменения факторов на признак-результат не надо соблюдать последовательность факторов. Основным условием при формировании индексов надо знать, что при построении индексов качественного состава необходимо индексируемую величину взвешивать по весам отчетного (текущего) периода. Индексы количественного состава соизмеряются при помощи соизмерителей базисного периода ( 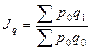 ).
).
Метод цепных подстановок
Этот метод предусматривает проведение нескольких расчетов для изучения количественного влияния факторов на признак-результат. Однако в отличие от первых двух методов в этом методе при расчете учитывается последовательность. Сначала рассчитывается влияние количественного фактора, затем структурного и в последнюю очередь качественного. В случае, если модель состоит из нескольких факторов одного и того же вида, то выбирается, логически, сначала более весомый фактор. Следующей особенностью этого метода является то, что в расчетах производится последовательная замена базовой величины каждого из факторов, его фактической величиной, остальные факторы остаются неизменными. Причем, при изучении влияния последующих факторов, предшествующие берутся на уровне отчетного периода, а остальные – на уровне базисного. Так, при изучении влияния 2-го фактора, 1-ый берется на уровне отчетного периода, а остальные на уровне базисного периода. При расчете влияния 3-го фактора первые два берутся на уровне базисного периода. При расчете влияния 4-го фактора первые три берутся на уровне отчетного периода, а остальные – на уровне базисного периода и т.д. Если порядок подстановки не соблюдается, то влияние каждого фактора искажается, а сумма влияния всех факторов совпадает с общим отклонением признака-результата.
Надо отметить, что при цепном методе подстановки производится на один расчет меньше чем факторов. Если факторов четыре производится три расчета, если факторов три – два расчета, если факторов два – один расчет. Цепной метод может применятся во всех моделях детерминированного анализа (см. табл. 11).
Покажем, на примере задачи (см. табл. 12) – цепной метод подстановки детерминированного фактора анализа.
В алгоритме данной задачи:  , первым фактором – количественным является
, первым фактором – количественным является  – численность работников предприятия, вторым структурным – d-доля рабочих среди всех работников предприятия, третьим фактором – качественным –
– численность работников предприятия, вторым структурным – d-доля рабочих среди всех работников предприятия, третьим фактором – качественным –  средняя выработка рабочих.
средняя выработка рабочих.
Многофакторная модель изменения выпуска продукции равна:

 – изменение выпуска продукции в отчетном периоде по сравнению с базисным
– изменение выпуска продукции в отчетном периоде по сравнению с базисным
за счет влияния:
 – численности работников предприятия
– численности работников предприятия
 – структуры рабочих среди всех работников предприятия
– структуры рабочих среди всех работников предприятия
 – средний выработки рабочих
– средний выработки рабочих
Рассмотрим изменение факторов на выпуск продукции за счет:
- Изменение численности работников

- Изменение доли рабочих среди всех работников предприятия

- Изменение средней выработки рабочих

Многофакторная модель изменения выпуск продукции равна:
 (см. гр. 7, табл. 12)
(см. гр. 7, табл. 12)
 – изменение выпуска продукции
– изменение выпуска продукции
за счет влияния:
 – численности работников предприятия
– численности работников предприятия
 – структуры рабочих среди всех работников предприятия
– структуры рабочих среди всех работников предприятия
 – средний выработки рабочих
– средний выработки рабочих
Термин «цепных подстановок» назван потому что вычитаемое первой разности –  равно вычитателю второй разности, а вычитаемое второй разности равно вычитателю третьей разности –
равно вычитателю второй разности, а вычитаемое второй разности равно вычитателю третьей разности –  . И производится только два расчета:
. И производится только два расчета:  и
и  .
.
Метод абсолютных разниц
Этот метод является упрощенным вариантом метода цепных подстановок. Абсолютное отклонение по первому фактору умножается на базовые значения остальных факторов. Затем абсолютное отклонение по второму фактору умножается на фактическое значение первого фактора и на базисные значения остальных факторов. В последующих расчетов абсолютное отклонение изучаемого фактора умножается на фактические значения предыдущих, рассмотренных факторов и на базисные значения последующих не рассмотренных факторов.
При использовании метода абсолютных и относительных разниц так же как и при методе цепных подстановок соблюдается последовательность расчета факторов. Этот метод может применятся в мультипликативных и смешанных моделях совмещающих мультипликативные и аддитивные модели (см.табл. 11).
На примере задачи (см. табл. 12) проиллюстрируем применение метода абсолютных разниц. Итак, многофакторная модель изменения выпуска составлена из следующих факторов:

Выпуск продукции в отчетном периоде по сравнению с базисным за счет:
- роста численности работников вырос на:

- увеличение доли рабочих среди работников вырос на:

- рост выработки рабочих вырос на:

Многофакторная модель изменения выпуска продукции равна:
 (см. гр. 8, табл. 12).
(см. гр. 8, табл. 12).
Метод относительных разниц
Метод относительных разниц основан на методе цепных подстановок и индексном методе.
При этом методе, используются только мультипликативные модели (см. табл. 11) как произведение относительных отклонений индивидуальных индексов по изучаемому фактору за минусом единицы на индивидуальные индексы рассмотренных факторов и на абсолютное значение фактора-результата в базовом периоде. Так, при изучении влияния первого фактора (соблюдается очередность расчета факторов) абсолютное значение признака-результата базового периода умножается на индивидуальный индекс первого фактора за минусом единицы. При изучении влияния второго фактора абсолютное значение признака-результата базового варианта умножается на индивидуальный индекс первого фактора и на индивидуальный индекс второго фактора за минусом единицы. При изучении влияния третьего фактора фактор-результат базового периода умножается на индивидуальный индекс первых двух факторов и на индивидуальный индекс третьего фактора за минусом единицы и т.д.
Рассмотрим на примере (см. табл. 12) применение этого метода.
Многофакторная модель равна:

Прирост выпуска продукции обеспечивается:
- влиянием 1-го фактора численности работников на:

- влиянием 2-го фактора-доли рабочих среди всех работников

- влиянием 3-го фактора-выборки рабочих

Многофакторная модель изменения выпуска продукции равна:
 (см. гр. 9, табл. 12).
(см. гр. 9, табл. 12).
Интегральный метод
При использовании интегрального метода очередность расчета факторов не имеет значения. Интегральный метод также как и другие математические методы (дифференциальный, логарифмический) убирают ту погрешность – совместного влияния факторов на признак-результат, которая присутствует при использовании предыдущих методов[7].
Интегральный метод применяется в мультипликативных, кратных и смешанных методах кратно-аддитивного вида (см. табл. 11).
В интегральном методе используется набор стандартных формул.
1. При двухфакторной мультипликативной модели:
 - интегральный
- интегральный
 – признак-результат
– признак-результат
 – признаки-факторы
– признаки-факторы
Метод влияния факторов равен:
 , где
, где
 и
и 
2. При 3-х факторной мультипликативной модели:  интегральный метод влияния факторов равен:
интегральный метод влияния факторов равен:
 , где
, где



Покажем этот метод на вышерассмотренном примере (см. табл. 12).
На выпуск продукции влияет изменение численности работников:



Влияние роста доли рабочих среди всех работников на рост выпуска продукции равно:



Рост выработки рабочих увеличивает выпуск продукции на:



Многофакторная модель изменения выпуска продукции равна:
 (см. гр.10 табл. 12)
(см. гр.10 табл. 12)
