Измерения Аристарха Самосского

Аристарх Самосский в своем труде «О величинах и расстояниях Солнца и Луны» рассказал о первых измерениях размеров и расстояний до Луны и Солнца.

Исходя из равенства видимых размеров Солнца и Луны он заключил, что при полном солнечном затмении Луга касается поверхности Земли самой вершиной своего теневого конуса (Рисунок 7).

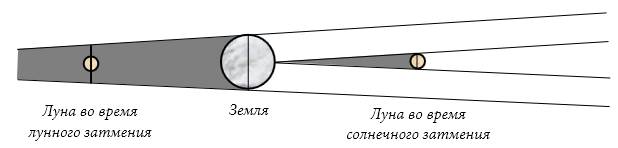
Рисунок 7 – Теневые конусы при затмениях.

Таким образом, на расстоянии от Земли до Луны поперечник земной тени уменьшается ровно на величину диаметра Луны. Из наблюдений уже лунных затмений получается, что Луна укладывается в земной тени ровно 3 раза, исходя из чего можно считать, что диаметр Луны в 3 раза меньше диаметра Земли, то есть порядка 2100 км (при точном значении в 1737 км).

Это измерение позволило оценить и расстояние от Земли до Луны в земных радиусах, которое составило примерно 76–80 земных радиусов (475–500 тысяч км), если принимать число π за 3 или за 22/7.

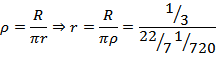
Где r – расстояние R – радиус Луны в Земных радиусах, ρ – угловой диаметр Луны в долях полного круга.

Для измерения расстояния до Солнца Аристарх использовал наблюдение о том, что если Луна освещена ровно наполовину, то вся система Солнце-Земля-Луна образует собой прямоугольный треугольник, то есть она находится в положении квадратуры (рисунок 8).

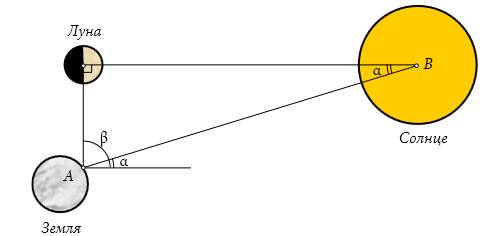
Рисунок 8 – Квадратура.

Таким образом, измерив угол β между направлениями Земля-Луна и Земля-Солнце в этот период времени можно получить расстояние от Земли до Солнца, выраженное в уже известных нам расстояниях от Земли до Луны. Аристарх получил значение угла в 87°, что дало соотношение расстояний в 1/20.

Но точное значение данного угла получить очень трудно, так как за 1 час угловое расстояние между луной и Солнцем меняется на ½°, что требует определения момента половинной освещенности Луны с соответствующей точностью. В реальности этот угол составляет 89°50’, в результате чего реальное значение отличается от значения, полученного Аристархом почти в 20 раз!