Задачи для самостоятельного решения. Режимы движения жидкости

Режимы движения жидкости. Гидравлические сопротивления. Уравнение Бернулли с учетом потерь энергии

Различают 2 режима движения жидкости: ламинарный и турбулентный, определяемые по безразмерному критерию – числу Рейнольдса Re

– для напорных потоков круглого сечения;

– для некруглых напорных потоков и безнапорных.

Граница, при которой происходит смена режимов – критическое число Рейнольдса Reкр, ему соответствует критическая скорость vкр.

Reкр= 2320 – для напорных потоков круглого сечения;

Reкр= 580 – для некруглых напорных потоков и безнапорных.

Тогда при Re < 2320 (580) – режим ламинарный;

при Re > 2320 (580) – режим турбулентный.

Общая потеря напора на рассматриваемом участке потока определяется

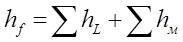
Потери напора по длине определяют по формуле Дарси-Вейсбаха

,

где – коэффициент гидравлического трения (коэффициент Дарси).

Местные потери напора определяют по формуле Вейсбаха

,

где – коэффициент местного сопротивления.

Для 2-х сечений потока реальной жидкости уравнение Бернулли будет иметь вид

Примеры решения задач

№ 1. По трубе диаметром 70 мм протекает за сутки 120 000 кг нефти плотностью 820 кг/м3, вязкость нефти = 0,5 см2/с.

Определить режим движения нефти.

Решение

;

Q = 120 000 / 820 ∙ 86 400 = 0,0017 м3/с;

= 3,14 ∙ 0,072 / 4 = 0,0038 (м2);

V = 0,0017 / 0,0038 = 0,45 (м/с);

Re = 45 ∙ 7 / 0,5 = 630 < Reкр = 2320 – режим ламинарный.

№ 2. Определить режим движения в лотке прямоугольного сечения шириной b = 120 см при уровне воды в нем h = 5 см, если v = 8 см/с, =0,015см2/с.

Решение

; = b ∙ h / 2h + b = 120 ∙ 5 / 2 ∙ 5 + 120 = 4,62 (см)

Re = 8 ∙ 4,62 / 0,015 = 2464 > Reкр= 580 – режим турбулентный.

№ 3. Определить потери напора на трение по длине водопровода диаметром 100 мм и длиной 2,5 км, если расход воды 11,8 л/с.

Найти гидравлический уклон этого трубопровода.

Решение:

; = 3,14 ∙ 0,12/ 4 = 0,00785 (м2).

V = 0,0118 / 0,00785 = 1,5 (м/с).

Принимается = 0,01 см2/с.

= 150 ∙ 10 / 0,01 = 150 000 > 2320 – режим турбулентный.

Принимаются стальные сварные новые трубы, эквивалентная шероховатость которых = 0,06 мм.

Определяется зона, в которой работает турбулентный поток:

10d / 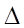= 10 ∙ 100 / 0,06 = 16 670;

500d / 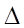= 500 ∙ 100 / 0,06 = 833 330;

10d / 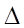= 16 670 < Re = 150 000 < 500d / 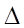= 833 330 – переходная зона.

Для определения коэффициента гидравлического сопротивления можно применить формулу Альтшуля

=

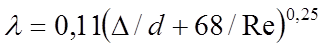= 0,11(0,06 / 100 + 68 / 150 000)0,25= 0,02;

hL= 0,02 ∙ 2500 / 0,1 ∙ 1,52 / 2 ∙ 10 = 56,3 (м).

Гидравлический уклон i = hL/ L = 56,3 / 2500 = 0,023 (м/м).

№ 4. Вода из одного бассейна в другой подается по новой стальной трубе диаметром 50 мм длиной 120 м с расходом 12 л/с. На трубе имеются местные сопротивления: вход в трубу, 2 колена под углом 900, полностью открытая задвижка, выход из трубы.

Определить разность уровней воды в резервуарах h. Построить напорную и пьезометрическую линии.

Составим уравнение Бернулли для сечений 1–1 и 2–2 относительно плоскости сравнения 0–0.

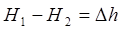; V1= V2= 0; V – скорость движения в трубопроводе;

; ;

Определяется скорость в трубе (м/с).

Определяется режим движения при кинематической вязкости воды

= 0,01см2/с. = 611∙ 5 / 0,01 = 305 500 – режим турбулентный.

Границы зон сопротивления (при эквивалентной шероховатости труб =0,1мм)

10d / 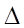= 10 ∙ 50 / 0,1 = 5000;

500d / 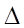= 500 ∙ 50 / 0,1 = 250 000;

Re = 305 500 > 500d / 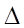= 250 000 – поток работает в зоне шероховатых русел, коэффициент гидравлического сопротивления определяется по формуле Шифринсона

Для определения потерь напора на местных сопротивлениях примем по справочнику коэффициенты местных сопротивлений:

вх= 0,5 – на входе в трубу;

пов= 1,19 – угол поворота 900;

з= 0,15 – задвижка полностью открытая;

вых= 1 – выход из трубы в резервуар.

(м).

Для построения линий Е–Е и Р–Р в характерных сечениях вычислим величины потерь напора:

примем, что длина вертикальных участков L1= L4 = 10 м, горизонтальный участок делится задвижкой на L2= 70 м, L3= 30 м;

для удобства вычислений найдем величину скоростного напора

v2/2g = 6,112/ 2 ∙ 10 = 1,867 (м);

а) в начале трубопровода – местные потери на входе в трубу

hм вх= вх∙ v2/2g = 0,5 ∙ 1,867 = 0,934 (м);

б) потери напора по длине на участке L1 (м);

в) местные потери на угле поворота

hм пов = пов∙ v2/2g = 1,19 ∙ 1,867 = 2,22 (м);

г) потери напора по длине на участке L2 (м);

д) местные потери на задвижке

hм з = з ∙ v2/ 2g = 0,15 * 1,867 = 0,28 (м);

е) потери напора по длине на участке L3 (м);

ж) местные потери на угле поворота

hм пов = пов∙ v2/ 2g = 1,19 * 1,867 = 2,22 (м);

з) потери напора по длине на участке L4 (м);

и) местные потери на выходе из трубы

hмвых= вых ∙ v2/ 2g = 1 ∙ 1,867 = 1,867 (м).

Суммарные потери напора

0,934 + 8,59 + 2,22 + 60,12 + 0,28 + 25,76 + 2,22 + 8,59 + 1,867 = 110,58 (м),

т.е. совпадают с величиной h = 110,6 (м).

Приняв горизонтальный и вертикальный масштабы на основе этих данных и известных правил строятся Е–Е (напорная) и Р–Р (пьезометрическая) линии.

Задачи для самостоятельного решения

№ 5. По трубопроводу диаметром 100 мм перекачивается нефть ( =0,42см2/с) в количестве 12дм3/с.

Определить: а) режим движения нефти;

б) критическую скорость.

№ 6. Определить потерю напора в трубопроводе длиной 500 м и диаметром 150 мм при перекачке воды расходом 20 л/с, = 0,012 см2/с.

№ 7. Как изменится потеря напора в трубопроводе (№ 2), если диаметр трубы уменьшится в 2 раза?

№8. Как изменится потеря напора в трубопроводе (№ 2), если вязкость уменьшится в 2 раза?

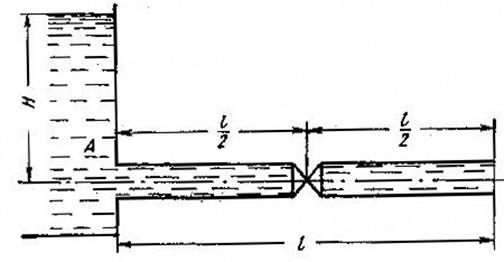
№ 9. К резервуару подсоединена труба длиной 60 м и диаметром 80 мм с вентилем посредине трубы.

Определить расход воды в трубе, если напор H = 8 м, = 0,025.

Построить Е–Е и Р–Р.

Ответы: № 5 – а) режим турбулентный;

б) 0,98 м/с;

№ 7 – увеличится в 16 раз;

№ 8 – уменьшится в 2 раза.