| Метод весов. |
Если число измеряемых навигационных параметров больше определяемых координат, то такие измерения называются избыточными. Избыточные измерения позволяют повысит точность обсервации и проконтролировать измерения на промахи. Т.к. измерения отягощены погрешностями, то высотные линии положения не пересекаются в одной точке, а образуют фигуру погрешностей. Известно, что погрешности подразделяются на случайные и систематические. - Чтобы учесть действие случайных погрешностей, надо применить метод весов (графический способ метода наименьших квадратов).
- Чтобы исключить систематические погрешности, надо провести астрономические биссектрисы.
Метод весов заключается в том, что каждой вершине фигуры погрешностей приписывется вес, вычисляемый по формуле Pij = 10sin2  Aij Aij  Aij - разность азимутов между i-ым и j-м светилами. Максимальный вес достигает 10 единиц при разности азимутов 90°. Вес показывает степень точности точки пересечения между ВЛП - чем выше вес, тем выше точность данной точки. Aij - разность азимутов между i-ым и j-м светилами. Максимальный вес достигает 10 единиц при разности азимутов 90°. Вес показывает степень точности точки пересечения между ВЛП - чем выше вес, тем выше точность данной точки. |
 | Для нахождения вероятнейшего места веса последовательно складываем центрографическим методом, т.е. находим центр тяжести фигуры, состоящей из невесомых стержней, в вершинах которой приложены найденные веса. Для данного примера складываем сначала веса 2 и 8, разделив сторону на 2 + 8 = 10 отрезков и отложив от большего веса (8) число отрезков, равным меньшему весу (2) и получаем точку с весом 10. Далее складываем два веса по 10, получив посредине между ними обсервованную точку с весом 20. Место по весам всегда получается внутри треугольника и лежит ближе к короткой стороне и ближе к прямому углу. |  | |
| |
| Два варианта ОМС по трем светилам. |
Рассмотрим два варианта расположения трёх светил и ОМС по этим светилам. Первый вариант. Пусть светила расположены равномерно по всему горизонту с разностью азимутов  А = 120°. Фигура погрешностей будет собой представлять равносторонний треугольник. Веса вершин будут равны 7. ОМС по весам будет в центре треугольника на пересечении биссектрис (высот, медиан). Астрономические биссектрисы также пересекаются внутри треугольника. Вывод: ОМС по весам совпадает с ОМС по астрономическим биссектрисам, следовательно, это самый идеальный вариант ОМС по 3-м светилам. Если светила располагаются ассиметрично, но по всему горизонту, то точки по весам и по астрономическим биссектирисам будут распологаться внутри треугольника вблизи друг от друга. А = 120°. Фигура погрешностей будет собой представлять равносторонний треугольник. Веса вершин будут равны 7. ОМС по весам будет в центре треугольника на пересечении биссектрис (высот, медиан). Астрономические биссектрисы также пересекаются внутри треугольника. Вывод: ОМС по весам совпадает с ОМС по астрономическим биссектрисам, следовательно, это самый идеальный вариант ОМС по 3-м светилам. Если светила располагаются ассиметрично, но по всему горизонту, то точки по весам и по астрономическим биссектирисам будут распологаться внутри треугольника вблизи друг от друга. |  | Второй вариант. Светила располагаются в одной части горизонта, разность между крайними азимутами составляет  А = 120°, а между соседними - А = 120°, а между соседними -  А = 60°. Фигура погрешностей также представляет собой равносторенний треугольник, в вершинах которого располагаются веса, равные 7. Поэтому ОМС по весам получается внутри треугольника (точка Мр). Астрономические биссектрисы же в этом случае пересекаются вне треугольника. (точка МАБ). Вывод: это самый неблагоприятный вариант расположения светил, поэтому надо исключить такой вариант расположения светил. Если же в силу гидрометеофакторов приходиться измерять высоты светил с такой конфигурацией азимутов, то для выбора ОМС необходимо руководствоваться следующими принципами: А = 60°. Фигура погрешностей также представляет собой равносторенний треугольник, в вершинах которого располагаются веса, равные 7. Поэтому ОМС по весам получается внутри треугольника (точка Мр). Астрономические биссектрисы же в этом случае пересекаются вне треугольника. (точка МАБ). Вывод: это самый неблагоприятный вариант расположения светил, поэтому надо исключить такой вариант расположения светил. Если же в силу гидрометеофакторов приходиться измерять высоты светил с такой конфигурацией азимутов, то для выбора ОМС необходимо руководствоваться следующими принципами: - Обсервованное место выбираем по принципу "Считай себя ближе к опасности".
- Если обсервация получена в океане и треугольник погрешностей образовался небольшим со сторонами не превышающими 1,5 м.миль, то считаем, что он образовался за счет действия случайных погрешностей (mВЛП = ±1,0 м.миль), поэтому обсервацию принимаем внутри треугольника, т.е. по весам.
- Если треугольник погрешностей оказался большим (стороны треугольника более 2 м.миль), то считаем, что он образовался за счет действия систематических погрешностей, поэтому обсервация принимается по астрономическим биссектрисам вне треугольника.
|  | |
| |
| Оценка точности ОМС по избыточным ВЛП. |
Оценку точности по избыточным ВЛП можно получить, применив метод наименьших квадратов. При равномерном распределении светил по всему горизонту рекомендуется удобная для запоминания формула, по которой вычисляется радиальная погрешность: 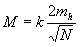 (4.5) k = 1 при симметричном расположении светил; k = 1,25 при отклонениях от симметричности; N - число линий положения. В среднем для трех ВЛП можно принимать M = 1,3mh, а для четырех ВЛП - M = 1,1mh (4.5) k = 1 при симметричном расположении светил; k = 1,25 при отклонениях от симметричности; N - число линий положения. В среднем для трех ВЛП можно принимать M = 1,3mh, а для четырех ВЛП - M = 1,1mh |
| |
| Достоинства и недостатки ОМС по 3-м светилам. |
| Если учитывать только случайные погрешности, то ОМС по 3-м ВЛП гораздо точнее (приблизительно на 20%), чем по двум светилам. Кроме того при ОМС по трем светилам исключаются систематические погрешности. Объём вычислений при ОМС по 3-м ВЛП на 50% больше объёма вычислений при ОМС по 2-м ВЛП. |
Наши рекомендации
 Aij
Aij  Aij - разность азимутов между i-ым и j-м светилами. Максимальный вес достигает 10 единиц при разности азимутов 90°. Вес показывает степень точности точки пересечения между ВЛП - чем выше вес, тем выше точность данной точки.
Aij - разность азимутов между i-ым и j-м светилами. Максимальный вес достигает 10 единиц при разности азимутов 90°. Вес показывает степень точности точки пересечения между ВЛП - чем выше вес, тем выше точность данной точки. 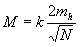 (4.5) k = 1 при симметричном расположении светил; k = 1,25 при отклонениях от симметричности; N - число линий положения. В среднем для трех ВЛП можно принимать M = 1,3mh, а для четырех ВЛП - M = 1,1mh
(4.5) k = 1 при симметричном расположении светил; k = 1,25 при отклонениях от симметричности; N - число линий положения. В среднем для трех ВЛП можно принимать M = 1,3mh, а для четырех ВЛП - M = 1,1mh 



