За пределами Галактики

16.1Вы, конечно, помните, как выглядят обычные фотографии туманности Андромеды (М31). Как вам кажется, каков примерно угол наклона плоскости галактики М31 к лучу зрения? После того как вы, никуда не заглядывая, сделали прикидку, проверьте себя, произведя необходимые измерения фотографии этой туманности в ответе.

16.2Как выглядела бы туманность Андромеды для невооруженного глаза, если бы мы видели ее с ребра?

16.3Оцените абсолютную звездную величину сверхновой, вспыхнувшей в 1987 г. в Большом Магеллановом облаке. В максимуме блеска она имела видимую звездную величину около 3^m.

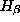16.4Ширина линии в спектре ядра сейфертовской галактики составляет около 30 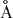. Каков разброс характерных скоростей движения облаков излучающего газа в ядре этой галактики?

16.5Радиоисточник в ядре активной галактики имеет угловой размер 0.001", величина красного смещения z = 0.5. Оцените линейные размеры источника в пк.

16.6Галактика удаляется от нас со скоростью 5000 км/с. Она видна как объект размером 1'. Оценить ее линейный размер.

16.7* Чего больше во Вселенной - протонов или реликтовых фотонов? Среднюю плотность вещества во Вселенной принять равной 10^-30 г/см³. Температура реликтового излучения равна 2.7 K.

Решения

Первое знакомство

1.1 Приравниваем объемы земного шара и проволоки:

где d -- диаметр проволоки, r -- расстояние до одного из указанных в условии объектов. Отсюда

Подставляя числа, находим диаметры "проволок", протянутых до Солнца и до 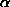Cen: 100 км и 200 м, соответственно. А в туманность Андромеды можно было бы ткнуть прутом толщиной 25 см! Согласитесь, вы ожидали, что "проволоки" окажутся значительно тоньше.

Обращаем внимание на то, что 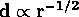. Проволоку толщиной в несколько миллиметров можно было бы дотянуть до самых далеких квазаров. Как видите, Вселенная совсем невелика!

А вот другая, в определенном смысле более правильная оценка того, велика ли на самом деле толщина нашей "проволоки", дотянутой до Солнца. Естественный масштаб в Солнечной системе задается ее собственным размером ( 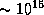см), а вовсе не размером человеческого тела ( 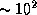см). Диаметр нашей "проволоки" (100 км= 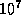см) составляет всего 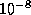от размера Солнечной системы. Поэтому она, если угодно, тоньше тончайшей паутины. Действительно, возьмем для сравнения человеческий волос. Его толщина 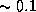мм= 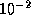см. Это 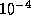от характерного размера тела человека. Поэтому в относительных единицах волос на четыре порядка толще нашего воображаемого космического шнура длиной 1 а.е. Интуиция, подсказывающая нам, что проволока, дотянутая до Солнца, должна быть очень и очень тонкой, все же нас не подводит.

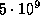1.2 На Земле живет человек. Число звезд в Галактике . Число галактик в наблюдаемой части Вселенной того же порядка: 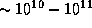(как получить эту оценку, пользуясь данными "Вселенной в числах"?). Поэтому в нашей Галактике на одного человека приходится всего несколько десятков звезд, а во всей Вселенной -- не более чем по сотне галактик.

1.3 На каждого землянина в Галактике приходится несколько десятков звезд (см. предыдущую задачу ). Не нужно быть энтомологом, чтобы сказать: комаров на каждого жителя Земли приходится гораздо больше. Если вы в этом сомневаетесь, съездите летом в тайгу.

Да что там комары! Легко прикинуть, что деревьев в сибирской тайге -- и то больше, чем звезд в Галактике. Площадь сибирской тайги 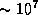км². Очевидно, что на одно дерево в тайге приходится меньше 100 м², а значит, деревьев больше, чем 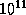. Кстати, это позволяет убедиться, что комаров на Земле гораздо больше, чем звезд в Галактике -- ведь под каждым деревом в тайге их ой-ой-ой сколько. Зимой в Сибири морозы, и комаров нет -- но их хватает во влажных тропических лесах.

1.4 В трехатомной молекуле H₂O на каждый атом приходится в среднем по 6 нуклонов, или по 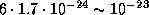г. Поэтому 1 см³ воды содержит 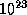атомов. Если принять, что во Вселенной 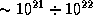звезд (см. задачу ), то диаметр капли воды с тем же числом атомов оказывается равен 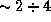мм.

1.5 Ньютонова сила все же больше кулоновой, но всего в несколько раз. Убедитесь в этом, приняв, что массы космонавтов -- по 100 кг (они ведь в скафандрах!), а расстояние между ними 1 м. Подсчет никакого труда не составляет, но результат впечатляет. Вы, конечно, знали, что гравитационное взаимодействие -- самое слабое из имеющихся в природе четырех фундаментальных взаимодействий. Но представляли ли вы себе, что оно настолько слабее электромагнитного?

1.6 Мы живем в нескольких вложенных друг в друга как матрешки потенциальных ямах.

Любой человек образует с Землей гравитационно-связанную систему с отрицательной энергией, в расчете на единицу массы равной 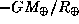. Глубина этой потенциальной ямы есть 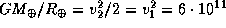эрг/г. Здесь 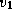и 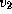-- соответственно первая и вторая космические скорости.

Имея в виду, что в космосе гравитационная энергия часто (например, при аккреции) переходит в энергию ионизации и возбуждения атомов, поучительно оценить глубину земной гравитационной потенциальной ямы в других единицах -- в эВ/нуклон: 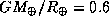эВ/нуклон (проверьте!).

А вот взгляд на те же вещи с совсем другой стороны. Чтобы отправить человека на Луну, необходимо преодолеть гравитационную энергию его связи с Землей. При массе тела в 70 кг (как у "среднего" космонавта) эта энергия составляет 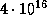эрг, или 4 ГДж. Это около 1000 киловатт-часов. Стоимость киловатт-часа 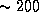руб. (цены конца 1996 г. для организаций -- вряд ли вы полетите на Луну как частное лицо). Поэтому оказывается, что энергия, которую надо затратить, чтобы вывести человека на просторы Солнечной системы, стоит всего 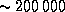рублей, или около 35 долларов. Выводы: 1) "накладные расходы" в космонавтике колоссальны; 2) экономическая яма, в которой мы сейчас оказались, гораздо глубже, чем гравитационная.

Далее, Земля со всеми своими обитателями образует гравитационно-связанную систему с Солнцем, а Солнце -- с Галактикой. Глубины соответствующих потенциальных ям найдите самостоятельно. Вот ответы: "солнечная" яма в 14, а "галактическая" -- в 1000 раз глубже "земной".

При оценке энергии, которую необходимо сообщить частице для выхода из этих потенциальных ям, не забудьте учесть, что Земля движется вокруг Солнца, а Солнечная система -- по своей близкой к круговой орбите в Галактике. Из-за этого требуемые энергии вдвое меньше глубин соответствующих потенциальных ям (докажите!). Так, выход с земной орбиты на галактические просторы требует примерно в 7 раз большей энергии, чем нужно для полета к Луне. Для вылета в метагалактику с нашей галактической орбиты потребуется дополнительно затратить еще 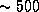"лунных" единиц энергии.

1.7 По определению, модулем расстояния m - M до объекта, находящегося на расстоянии r (в парсеках), называется величина

С учетом того, что 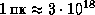см, а расстояние от Санкт-Петербурга до Москвы 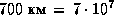см, что в парсеках составляет 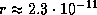, находим, что соответствующий ему модуль расстояния равен .

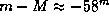Проверьте самостоятельно, что модуль расстояния в 1 см равен .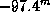

Главное, что нужно уяснить: модуль расстояния, хотя и выражается в звездных величинах, никакого отношения к излучению не имеет. Это просто одна из возможных, и притом удобных для астрономии внесистемных единиц измерения расстояний. (Ср. со световым годом, где расстояние измеряется в единицах времени.) Удобство использования логарифмической шкалы звездных величин для измерения расстояний во Вселенной объясняется колоссальным разбросом расстояний до различных астрономических объектов.

1.8

Самые яркие звезды Плеяд горячие -- ведь звезды ковшика Плеяд явно белые, даже голубоватые. Поскольку Плеяды -- это рассеянное звездное скопление, эти горячие звезды лежат на главной последовательности.

Звезды поздних подклассов B имеют абсолютную звездную величину, равную нулю, и они "белые". Голубые звезды имеют еще большую светимость -- а потому отрицательную абсолютную звездную величину, которая, таким образом, меньше солнечной по крайней мере на 5 единиц. Но звезды Плеяд при наблюдении из окрестностей Солнца имеют 4-ю видимую звездную величину. Значит, Солнце при наблюдении с Плеяд будет иметь, как минимум, 9-ю. Невооруженным глазом его видно не будет.

Хотя ответ и получен, стоит сделать еще один шаг и уточнить найденную оценку. Согласно Аллену [1], расстояние до Плеяд составляет 127 пк, а по новейшим данным ( HIPPARCOS) оно равно 117 пк. Поэтому видимая звездная величина Солнца при наблюдении его оттуда будет

m = M - 5 + 5 lg r = 4.8 - 5 + 5 lg 117 10.1^m,

что подтверждает сделанное ранее заключение. Солнце не увидеть с Плеяд не только простым глазом, но и в бинокль.

1.9 Первый ответ, который приходит в голову, -- "Конечно, угловой размер диска Луны больше". Ясно, что он должен быть неверен, иначе задачу не включили бы в сборник. Итак, оценим угловой размер туманности Андромеды. Расстояние до этой галактики 700 кпк. В качестве значения ее диаметра возьмем диаметр нашей Галактики, 30 кпк. Тогда искомая величина будет равна радиана, или .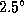

Таким образом, угловой размер туманности Андромеды почти в пять раз больше углового диаметра Луны! Мы не видим спирали в Андромеде простым глазом только из-за ее низкой поверхностной яркости, углового же разрешения глаза для этого вполне хватает.

1.10 Если бы звезды заполняли бесконечное евклидово пространство в среднем равномерно, то все небо имело бы такую же яркость, как и у диска Солнца. Действительно, телесный угол, под которым видны диски звезд, находящихся между r и r+dr, равен объему шарового слоя 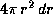, умноженному на число звезд в единице объема 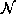и на телесный угол, под которым видна каждая из звезд (мы молчаливо предполагаем, что все они одинаковы; отказ от этого предположения не меняет конечного заключения). Последний равен, очевидно,

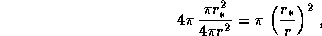
где 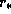-- радиус звезды. Итак, звезды из шарового слоя 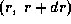занимают на небе телесный угол 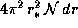. При интегрировании по r получается бесконечный телесный угол, так что диски звезд должны перекрываться, полностью покрывая собой небо. Если бы мир был так устроен, то день не отличался бы от ночи, а диск Солнца разглядеть на сверкающем небе было бы невозможно.

Это знаменитый фотометрический парадокс Ольберса (в действительности он был впервые сформулирован за век до Ольберса современником Ньютона Эдмундом Галлеем). Итак, из того, что по ночам темно, можно сделать весьма важное заключение о строении Вселенной, именно, что сделанные выше предположения не выполняются.

Разрешение фотометрического парадокса Галлея--Ольберса в том, что Вселенная расширяется, а потому нужно учитывать красное смещение. Подробнее объяснять здесь не место.

Кинематика неба

2.1 Достаточно, загорая, проследить за направлением суточного движения Солнца. Если утром (вы только что проснулись!) оно перемещается, как обычно, вверх и вправо, -- вы в северном полушарии. Если же вверх и влево -- то в южном. А если прямо вверх -- вы где-то у самого экватора.

Зачем в условии задачи упомянуто, что дело было 21 марта ?

2.2 Если в северном полушарии зима, то склонение Солнца отрицательно, и при наблюдении с экватора его суточное движение происходит привычным нам образом -- слева направо. В летнее же для европейцев время года 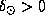, и суточное перемещение Солнца по небу при наблюдении с экватора происходит справа налево. Поэтому установить, что в Петербурге -- зима или лето -- особого труда не составит.

2.3 Убедитесь в том, что первобытные люди не очень агрессивны, понимают вашу речь и готовы вас внимательно слушать. Затем вспомните простые свидетельства шарообразности Земли, известные еще Аристотелю. Например, скрывающиеся под горизонтом силуэты кораблей. Или дождитесь лунного затмения, объясните, почему оно проиcходит и покажите, что тень Земли круглая.

С осевым вращением Земли дело обстоит сложнее. Смена дня и ночи, суточное вращение небесной сферы и другие подобные явления не убедят собеседников, что вращается именно Земля. Доказательствами могут служить механические эксперименты и наблюдения, указывающие на присутствие сил инерции, действующих в неинерциальных системах отсчета. Не произнося столь мудреных терминов, залезьте на дерево и попробуйте, привязав камень к веревке, сделать маятник Фуко. Если дело происходит не очень близко к экватору, эксперимент, быть может, удастся.

2.4 Вспомните, что прецессию иначе называют предварением равноденствий (латинское слово "praecessio" означает "предварение"). Следующее равноденствие наступает раньше предыдущего. Значит, точка весны движется навстречу Солнцу. Но Солнце в своем годичном движении перемещается с запада на восток. Следовательно, точка весны движется с востока на запад, т.е. слева направо в северном полушарии Земли и справа налево -- в южном.

2.5 В России Солнце всегда кульминирует к югу от зенита. Поэтому можно воспользоваться следующей формулой для высоты светила в верхней кульминации:

где 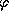-- широта места, 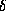-- склонение светила. Учтем также, что склонение Солнца в течение года меняется в пределах

где 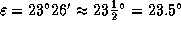-- наклон эклиптики к экватору. (Обращаем внимание, что на самом деле 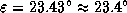, а вовсе не 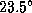). Имеем поэтому

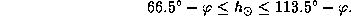
Например, в Петербурге ( )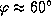

В какие дни достигаются эти пределы?

А что будет, если судьба забросила нас из России, скажем, на юг Индии?

2.6 Оценим время захода с точностью до получаса. Часовой угол Солнца при заходе определяется из формулы

Широта места 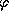должна быть известна. Склонение Солнца 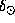либо оцените сами по дате, либо возьмите из Ежегодника. Например, для Петербурга 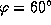и, скажем, 5 ноября 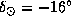, так что 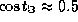, и 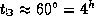. Значит, Солнце зайдет через 4 часа после истинного полудня. Истинный полдень наступит около 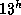по московскому времени (см. задачу ). Следовательно, Солнце зайдет около .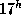

2.7 Если вы человек изворотливый и немного знаете географию, то и почти ничего не смысля в сферической астрономии, сразу же скажете, что дело было в Армавире. Действительно, ясно, что нам предлагается вывести некую формулу, в которую будет входить широта места наблюдения 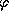. Понятно, что широта будет аргументом у какой-то тригонометрической функции -- синуса, косинуса или тангенса. Из стиля задачника ясно, что значение 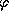должно быть таким, чтобы все расчеты можно было сделать без калькулятора. Значит, 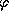либо 45^o, либо 60^o. Но 60^o не подходит -- это широта Петербурга, а не Арзамаса (и тем более не Армавира). Значит, 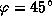, а это явно не Арзамас -- он заметно севернее. Итак, ответ должен быть -- Армавир. Это правильный ответ.

Все это, конечно, несерьезно, хотя иногда в жизни подобная сообразительность сильно помогает. Впрочем, мало кто решается на такое нахальство, когда речь идет о формулах, -- а зря, как мы только что убедились.

Вот настоящее решение. По определению точки весеннего равноденствия, 21 марта имеем 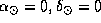. Воспользуемся формулой из решения предыдущей задачи

Найдем, как изменяется 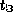при малом изменении 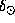. Дифференцируя, получаем

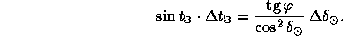
Но в день весеннего равноденствия 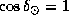, и Солнце заходит точно на западе, так что 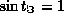. Поэтому около 21 марта 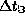и 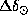связаны так:

За один день Солнце проходит по эклиптике 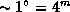(на самом деле чуть меньше, 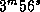). Поэтому около 21 марта для изменения 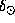за 1 день мы имеем

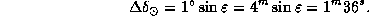
Но согласно условию задачи, 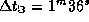. Поэтому

так что 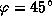. Это -- Армавир, он находится практически точно на 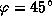. Арзамас же лежит на 10 градусов севернее, точнее, на 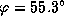, так что для него 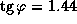. Солнце в Арзамасе 22 марта заходит на 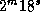позже, чем накануне -- весьма заметная разница по сравнению с Армавиром.

2.8 Незаходящие светила -- те, у которых высота нижней кульминации

т.е. звезды со склонениями

На рисунке показана проекция небесной сферы на плоскость небесного меридиана.

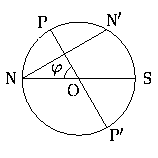
Незаходящие звезды заполняют сегмент 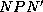. Площадь этого сегмента есть 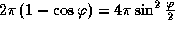, а площадь всей небесной сферы составляет 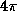. Доля незаходящих звезд равна отношению этих площадей, т.е. .

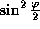Частные случаи:

• на полюсе ( 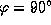) половина звезд никогда не заходит;
• на экваторе ( 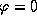) все звезды восходят и заходят;
• в Петербурге ( 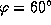) доля незаходящих звезд равна 1/4.

2.9 22 июня на северном полюсе Солнце круглые сутки находится на высоте _~23¹/₂^o над горизонтом. Поскольку в полнолуние Луна находится почти в противоположной Солнцу точке небесной сферы, она будет все время примерно на такой же высоте под горизонтом и, следовательно, видна не будет.

Чтобы обосновать ответ более аккуратно, вспомним, что наклон плоскости орбиты Луны к плоскости эклиптики составляет около 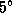. Поэтому Луна 22 июня будет как минимум в 23¹/₂^o - 5^o = 18¹/₂^o под горизонтом. Если полнолуние придется даже на 1 июня, Луна все же видна не будет (почему?).

2.10 Видимые цвет и яркость Луны -- это, разумеется, эффект прохождения лучей от Луны через земную атмосферу: у горизонта атмосферное ослабление велико (особенно для синих лучей). Луна видна тусклой и желтоватой. Так что достаточно объяснить, почему зимой в полнолуние Луна кульминирует высоко, а летом -- низко над горизонтом.

В полнолуние Луна -- в направлении, противоположном направлению на Солнце (если пренебречь небольшим, 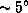, наклоном ее орбиты к плоскости эклиптики). Значит, полная Луна в полночь зимой примерно там, где Солнце -- летом в полдень. Все знают, что летом Солнце в полдень стоит высоко, а зимой низко. Луна же, понятно, наоборот.

2.11 Поскольку наклон плоскости орбиты Луны к плоскости эклиптики 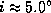, склонение Луны в течение периода прецессии линии узлов (18.6 года) изменяется в пределах

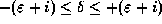
где 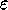= 23¹/₂^o -- наклон эклиптики к экватору, так что

.

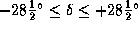Далее решение аналогично решению задачи . Например, в Петербурге (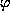 = 60^o) для высоты Луны в верхней кульминации имеем неравенства

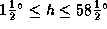
Бывают, следовательно, периоды времени, когда Луна в Петербурге не поднимается выше полутора градусов над горизонтом. Когда это бывает -- летом или зимой?

А "лунный северный полярный круг" проходит на широте около 61¹/₂^o. Севернее лежит зона, где хотя бы раз в 18.6 года Луна в полнолуние не восходит вовсе.

2.12 В зените кульминируют светила с 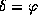. Так как склонение Луны всегда заключено в пределах (см. решение задачи )

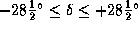
а самая южная точка России имеет широту около 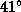, Луна в России наблюдаться в зените не может.

2.13 Когда Луна в последней четверти, она видна на небе вблизи апекса орбитального движения Земли (поясните это чертежом). Следовательно, звезды, находящиеся на небесной сфере неподалеку от Луны, в среднем (только в среднем!) приближаются к нам со скоростью орбитального движения Земли, 30 км/с.

Впрочем, мы были немного неточны. Под термином "лучевая скорость звезды" обычно понимают ее лучевую скорость относительно барицентра Солнечной системы. Поэтому в формулировке задачи следовало указать, что речь идет о непосредственно измеряемых лучевых скоростях, не исправленных за движение Земли.

2.14 Дата 7 февраля "равноудалена" от дней зимнего солнцестояния и весеннего равноденствия, так что прямое восхождение Солнца равно 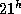. Поскольку Луна в последней четверти, ее прямое восхождение на 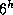меньше и, значит, равно .

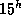2.15 Выясним условия видимости созвездий в Петербурге в настоящее время. У Ориона 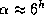, что означает верхнюю кульминацию в полночь зимой. Высота в верхней кульминации такая же, как у Солнца в конце марта, т.е. 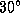. У Южной Короны 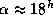, что означает верхнюю кульминацию в полночь летом, а высота в верхней кульминации составит примерно 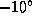. Таким образом, созвездие Ориона хорошо видно зимой, а Южная Корона не видна вовсе.

13 000 лет -- половина периода прецессии. За это время плоскость экватора, составляющая угол 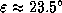с плоскостью эклиптики, повернется на полоборота вокруг оси эклиптики. (Сделайте чертеж небесной сферы и нанесите на него эклиптику, положения экватора сейчас и через 13 000 лет; отметьте также положение обоих созвездий.) Вследствие прецессии экваториальные координаты Ориона через 13 000 лет составят

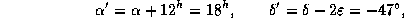
а координаты Южной Короны станут

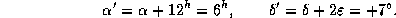
(Убедитесь в правильности этих формул по чертежу.)

Поэтому через 13 000 лет созвездие Ориона будет в верхней кульминации в полночь летом, а высота его в кульминации составит -17^o, так что знаменитый пояс Ориона и другие красоты этого созвездия станут недоступны петербуржцам. Зато Южная Корона, невидимая сейчас, будет хорошо видна в Петербурге зимой, кульминируя на высоте 37^o.

2.16 Начало, если дело происходит в северном полушарии на широте 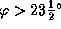, и конец в противном случае. Действительно, 22 июня в северном полушарии на широтах 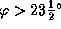и Солнце, и Луна перемещаются по эклиптике справа налево. При этом Солнце обходит всю эклиптику за год, а Луна -- за месяц. Поэтому Луна догоняет Солнце, и в начале затмения ее диск наползает на Солнце справа.

Кстати, подобное наивное "геоцентрическое" описание солнечного затмения позволяет легко оценить его наибольшую возможную продолжительность (от первого до четвертого контакта): если за месяц, точнее, за синодический месяц, т.е. за 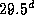, Луна смещается по эклиптике относительно Солнца на 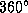, то 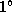-- сумму угловых диаметров дисков Солнца и Луны -- она пройдет за 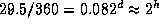. При такой грубой оценке наклоном лунной орбиты к плоскости эклиптики 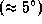вполне можно пренебречь. Одна существенная неточность в только что сделанной оценке, впрочем, все же есть: мы не учли вращение Земли. "Подправьте" наше решение самостоятельно.

2.17 Для наступления хотя бы частного солнечного затмения необходимо, чтобы угловое расстояние центра диска Луны от центра диска Солнца не превосходило суммы угловых радиусов Луны и Солнца, т.е. 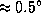. Поскольку центр диска Солнца движется по эклиптике, это условие можно переформулировать так: топоцентрическая эклиптическая широта Луны должна быть не более 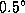. Так как горизонтальный суточный параллакс Луны составляет 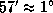, а параллаксом Солнца 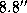можно пренебречь, геоцентрическая эклиптическая широта Луны должна быть не более .

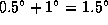Теперь рассмотрим прямоугольный сферический треугольник, вершинами которого служат центр диска Луны M, центр диска Солнца S и узел лунной орбиты 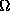(см. рис.). Сторонами треугольника являются дуги эклиптики, орбиты Луны и большого круга, проходящего через центры дисков Луны и Солнца и полюсы эклиптики. Угол при центре Солнца прямой.

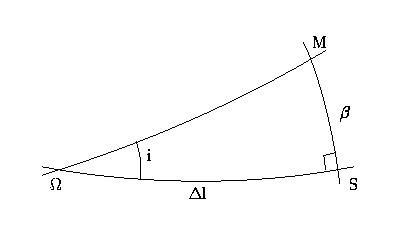
Острый угол при узле лунной орбиты есть наклон орбиты к плоскости эклиптики, 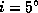. Катеты треугольника равны расстоянию Солнца от узла 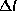и геоцентрической эклиптической широте Луны 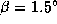. Треугольник с хорошей точностью можно считать плоским и узким, так чт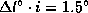о . Но 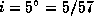рад. Поэтому .

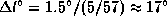2.18 Задача интересна в "бытовом" смысле: любопытно, на сколько отличается от 12 часов момент наступления "настоящего" полудня -- момента, когда Солнце выше всего, тени от предметов ориентированы строго на север или на юг (куда именно -- на север или на юг -- зависит от широты места и времени года; разберитесь в этом самостоятельно) и т. д.

Для определенности предположим, что сегодня 10 ноября, и вы находитесь в Петербурге.

Истинный полдень -- момент, когда истинное солнечное время 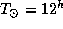. Среднее солнечное время составит 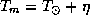, где 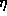-- уравнение времени. Воспользовавшись графиком, дающим уравнение времени на разные даты (см., например, [2], рис. 14), найдем, что 10 ноября 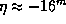. Следовательно, .

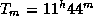Всемирное время 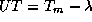, а долгота центра Петербурга 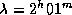, так что .

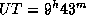Следующий шаг -- вычисление поясного времени. Петербург находится во втором часовом поясе, поэтому .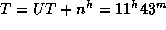

Наконец, вспомним, что в России действует декретное время, которое на один час впереди поясного. Летнее время, добавляющее еще час, 1-го ноября не действует, поэтому московское время совпадает с декретным. Окончательно получаем

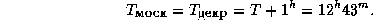
2.19 Так как солнечное время отсчитывается от полуночи, то когда в Гринвиче 0^h, там полночь, т.е. Солнце -- в нижней кульминации. В верхней же кульминации оно будет в этот момент на противоположной стороне земного шара, так что долгота места наблюдения равна 12^h.

2.20 a) Период колебаний маятника длиной l дается формулой Гюйгенса

где 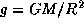-- ускорение свободного падения, G -- гравитационная постоянная, M -- масса Земли, R -- расстояние от центра Земли в точке, где находится маятник. Таким образом,

так что

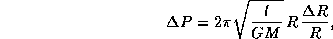
откуда

От экватора к полюсу 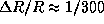, и значит, 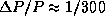. За сутки часы уйдут на .

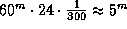б) Изменение периода, обусловленное изменением l, приближенно равно

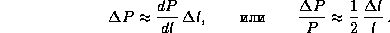
Поэтому требуемое для компенсации изменения хода часов изменение длины маятника

При длине маятника 1.5 м на полюсе его следует удлинить на 1 см.