Некоторые частные случаи движения точки
Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки.
Равномерное прямолинейное движение
Равномерное прямолинейное движение - это движение, при котором тело за любые равные промежутки времени совершает равные перемещения, т. е. это движение с постоянной по модулю и направлению скоростью:
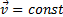 — уравнение скорости,
— уравнение скорости,
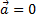 — уравнение ускорения.
— уравнение ускорения.
Пусть в момент времени t0=0 координата тела х0, в момент t - х (рис. 14).
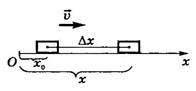
Рис.14
Тогда за промежуток времени Δt=t-t0=t координата X тела изменилась на величину ∆х = х - х0. Следовательно, проекция скорости тела
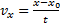 ,следовательно,
,следовательно,
x=x0+vxt- кинематическое уравнение равномерного движения (уравнение зависимости координаты от времени).
Проекция перемещения ∆rx=х-х0
∆rx=vxt - уравнение перемещения.
При равномерном прямолинейном движении направление скорости не изменяется, поэтому путь 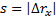 . Следовательно,
. Следовательно, 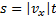 — уравнение пути.
— уравнение пути.
Зависимость кинематических величин от времени можно изобразить графически.
Изобразим графики скорости, перемещения, пути и координаты для трех тел: 1, 2, 3 (рис. 15).
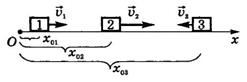
Рис.15
Тела 1, 2 движутся в положительном направлении оси Ох, причем 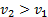 ; тело 3 движется в направлении, противоположном оси Ох; их начальные координаты соответственно
; тело 3 движется в направлении, противоположном оси Ох; их начальные координаты соответственно 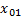 ,
, 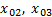 . Графики скорости представлены на рис.16. Площадь заштрихованного прямоугольника численно равна пути s (модулю перемещения), пройденному телом 1 за время t1. На рис.17 даны графики перемещения
. Графики скорости представлены на рис.16. Площадь заштрихованного прямоугольника численно равна пути s (модулю перемещения), пройденному телом 1 за время t1. На рис.17 даны графики перемещения 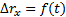 , на рис.18 - графики пути s=f(t).
, на рис.18 - графики пути s=f(t).
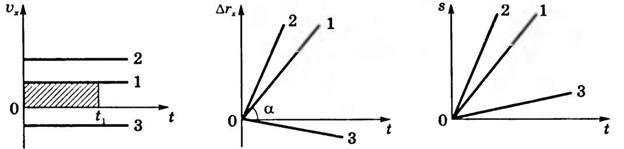
Рис.16 Рис.17 Рис.18
Наклон графика 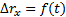 , к оси времени зависит от модуля скорости:
, к оси времени зависит от модуля скорости: 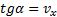 .
.
Графики движения (зависимости координаты от времени) изображены на рис.19.
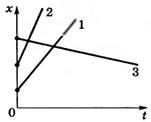
Рис.19
С помощью графика движения можно определить:
1) координаты тела в любой момент времени;
2) путь, пройденный телом за некоторый промежуток времени;
3) время, за которое пройден какой-то путь;
4) кратчайшее расстояние между телами в любой момент времени;
5) момент и место встречи тел и др.
Равноускоренное прямолинейное движение
Равноускоренное прямолинейное движение - это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.
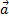 =сonst — уравнение ускорения.
=сonst — уравнение ускорения.
По определению ускорения 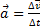 .
.
Пусть в момент времени t0 скорость тела равна 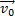 , в момент времени t -
, в момент времени t - 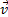 . Тогда за промежуток времени ∆t=t-t0=t скорость изменилась на
. Тогда за промежуток времени ∆t=t-t0=t скорость изменилась на 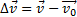 . Следовательно, ускорение
. Следовательно, ускорение 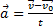
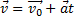 — уравнение скорости.
— уравнение скорости.
Или в проекциях: 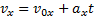 .
.
Эти зависимости кинематических величин от времени изобразим графически для трех тел (рис.20).
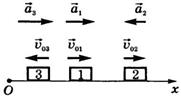
Рис.20
Графики ускорения 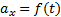 представлены на рис.21, а графики скорости
представлены на рис.21, а графики скорости 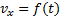 - на рис.22.
- на рис.22.
Для нахождения перемещения воспользуемся графиком скорости (рис.23). Для малого промежутка времени ∆t изменением величины скорости можно пренебречь и скорость можно считать постоянной. Тогда перемещение за промежуток времени ∆t будет равно площади узкой густо заштрихованной полоски. Мысленно разбив все время движения тела на малые промежутки времени и найдя перемещение за каждый отдельный промежуток времени, суммируем эти перемещения. Модуль проекции перемещения за промежуток времени ∆t=t-t0=t в пределе численно равен площади заштрихованной трапеции.
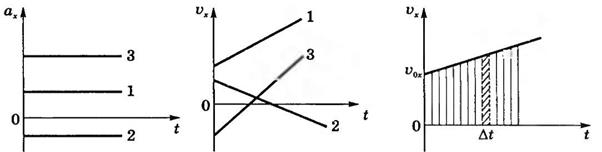
Рис.21 Рис.22 Рис.23
Следовательно, 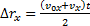 (2)
(2)
Подставив значение 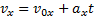 в (2), получим:
в (2), получим:
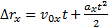 — уравнение перемещения в проекциях;
— уравнение перемещения в проекциях;
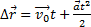 — уравнение перемещения в векторном виде.
— уравнение перемещения в векторном виде.
Учитывая, что х=х0+∆rх, имеем:
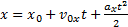 — кинематическое уравнение равноускоренного движения.
— кинематическое уравнение равноускоренного движения.
Его векторный вид: 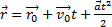
Исключая из уравнений скорости и перемещения время t, получим:
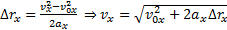 .
.
Сравнивая выражение (2) с формулой 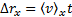 , найдем:
, найдем:
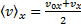 - проекция средней скорости при равноускоренном движении.
- проекция средней скорости при равноускоренном движении.
Графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения (рис.24).
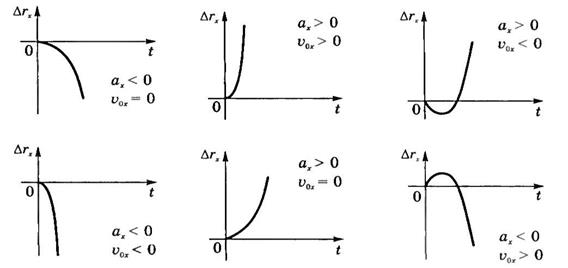
Рис.24
