Закон всемирного тяготения
Глава 5
Тяготение. Элементы теории поля
Законы Кеплера.
Закон всемирного тяготения
Еще в глубокой древности было замечено, что в отличие от звезд, которые неизменно сохраняют свое взаимное расположение в пространстве в течение столетий, планеты описывают среди звезд сложнейшие траектории. Для объяснения петлеобразного движения планет древнегреческий ученый К. Птоломей (II в. н.э.), считая Землю расположенной в центре Вселенной, предположил, что каждая из планет движется по малому кругу (эпициклу), центр которого равномерно движется по большому кругу, в центре которого находится Земля. Эта концепция получила название птоломеевой геоцентрической системы мираи при поддержке католической церкви господствовала почти полторы тысячи лет.
В начале XVI в. польским астрономом Н. Коперником (1473—1543) обоснована гелиоцентрическая система(см. § 5), согласно которой движения небесных тел объясняются движением Земли (а также других планет) вокруг Солнца и суточным вращением Земли. Теория и наблюдения Коперника воспринимались как занимательная фантазия.
К началу XVII столетия большинство ученых убедилось, однако, в справедливости гелиоцентрической системы мира. И. Кеплер (1571 — 1630), обработав и уточнив результаты многочисленных наблюдений датского астронома Т. Браге (1546—1601), изложил законы движения планет:
1. Планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.
2. Радиус-вектор планеты за равные промежутки времени описывает одинаковые площади.
3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит.
Впоследствии И. Ньютон, изучая движение небесных тел, на основании законов
Кеплера и основных законов динамики открыл всеобщий закон всемирного тяготения:между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек (m1 и m2) и обратно пропорциональная квадрату расстояния между ними (r2):
F=Gm1m2/r2. (22.1)
Эта сила называется гравитационной(или силой всемирного тяготения).Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Коэффициент пропорциональности G называется гравитационной постоянной.
Закон всемирного тяготения установлен для тел, принимаемых за материальные точки, т. е. для таких тел, размеры которых малы по сравнению с расстоянием между ними. Если же размеры взаимодействующих тел сравнимы с расстоянием между ними, то эти тела надо разбить на точечные элементы, подсчитать по формуле (22.1) силы притяжения между всеми попарно взятыми элементами, а затем геометрически их сложить (проинтегрировать), что является довольно сложной математической задачей.
Впервые экспериментальное доказательство закона всемирного тяготения для земных тел, а также числовое определение гравитационной постоянной G проведено английским физиком Г. Кавендишем (1731 —1810). Принципиальная схема опыта Кавендиша, применившего крутильные весы,представлена на рис. 37. Легкое коромысло А с двумя одинаковыми шари-
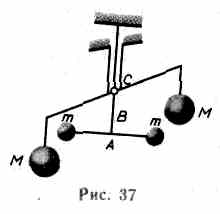
ками массой m = 729 г подвешено на упругой нити В. На коромысле С укреплены на той же высоте массивные шары массой М=158 кг. Поворачивая коромысло С вокруг вертикальной оси, можно изменять расстояние между шарами с массами m и M. Под действием пары сил, приложенных к шарам m со стороны шаров M, коромысло А поворачивается в горизонтальной плоскости, закручивая нить В до тех пор, пока момент сил упругости не уравновесит момента сил тяготения. Зная упругие свойства нити, по измеренному углу поворота можно найти возникающие силы притяжения, а так как массы шаров известны, то и вычислить значение G.
Значение G, приводимое в таблицах фундаментальных физических постоянных, принимается равным 6,6720•10-11Н•м2/кг2, т.е. два точечных тела массой по 1 кг каждое, находящиеся на расстоянии 1 м друг от друга, притягиваются с силой 6,6720-10-11Н. Очень малая величина G показывает, что сила гравитационного взаимодействия может быть значительной только в случае больших масс.
