Аддитамент тәсілі бойынша кішісфералық үшбұрыштарды есептеу

Егер сфералық үшбұрыштың қабарғаларының өлшемі 100 км аспаса, онда оны жазықтықтағы аддитаменттің кіші түзетулерін енгізу жолы арқылы бастапқы сфералық қабырғалары мен сфералық бұрыштарының теңестірілген жазық тригонометрия формулаларымен есептеуге болады.

Өлшенген бұрыштары арқылы қабырғаларын есептеу үшін сфералық тригонометрия формуласын жазайық:

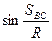
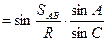(32)_;

Содан кейін есептеулерін бірінші мүшелерімен шектеп тригонометриялық қатарға бөлеміз:

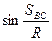
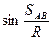
немесе

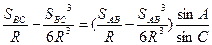(33)

Белгілейік

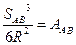
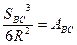(34)

(А өсімшесі қабырғаның аддитаменті деп аталады).

және

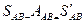
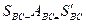(35)

онда

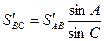
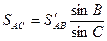(36)

Сондықтан, сфералық тригонометрия (32)формулаларымен есептеу тәсілі жазық тригонометрия формулаларын (З6) алмастырады.

Сол себепті сфералық үшбұрышты аддитамент тәсілімен есептеу үшін келесі амалдарды орындау қажет:

1) (34) формуласы арқылы бастапқы қабарғаның А аддитаментін есептеп оны бастапқы қабырғадан алып тастау қажет, соған байланысты бастапқы қабырға қосымша жазықтыққа ауысады

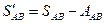2) келтірілген бастапқы қабырға арқылы 5д_Ь л сфералық үшбұрыштың қалған қабырғаларын да жазық тригонометрия формулаларымен есептейді. Фигураның шартына қатысты сфералық бұрыштар алдын ала түзетілуі қажет, сол себепті үшбұрыштың қиыспаушылығы (27) формуласымен есептеліп, әр бұрышына тең таратылады.

3) келтірілген әр қабырға үшін (34) формуласымен аддитаменті есептеледі, оны келтірілген қабырғаға қосады, содан үшбұрыштың сфералық қабырғалары есептеледі.

Жоғарыда келтірілген формулалар арқылы қабырғалары 100 км аспайтын үшбұрыштарды аддитамент тәсілімен сфералық үшбұрыштарды есептеу үшін арналған.

Абырғалары белгілі кішісфералық үшбұрыштарды есептеу тәсілі

Соңғы жылдары радиоқашықтықөлшеуіш және жарыққашықтықөлшеуін техникаларының пайда болуына байланысты трилатерация торларын құру кезінде тек қабырғаларын ғана өлшеу мүмкіндігі пайда болды. Сол себепті, сфералық үшбұрыштарды берілген қабырғаларымен есептеу қажеттілігі туындайды.

Жоғарыда жазылған сфералық үшбұрыштарды үшбүрыштар теориясын берілген қабырғаларына байланысты келесі ретпен есептеуге болады:

1) жазық үшбұрыштың бұрыштарын өлшенген сфералық қабырғалары арқылы жазық тригонометрия формуласымен есептеуге болады:

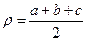(37)

мұнда α,β,с - үшбұрыштың сфералық қабырғалары;

ρ - үшбұрыштың жарты периметрі;

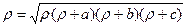(38)

мұнда Р – сфералық үшбұрыштың ауданы;

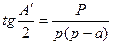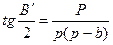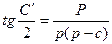, , (39)

мұнда Α′, В', С'- үшбұрыштың жазық бұрыштьары.

2) үшбұрыштың сфералық артықшылығын есептеу

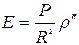(40)

3) үшбұрыштың сфералық бұрыштарын есептеу

A=A′+Е/3, B=B′+Е/3, C=C′+Е/3

Ал (37) - (40) формулалары қабырғалары 250 км болатын үшбұрыштарды есептеу үшін қолданады.

Ортынды

Қабырғалары 250 км аспайтын кіші сфералық үшбұрыштарды рационалды тәсілдермен есептеу үшін қолданылатын тәсілдердің негізі ретінде Лежандр және аддитамент тәсілдерін қолдану негізі сфералық үшбұрыштардың сфералық бұрыштары мен үшбұрыштың сфералық қабырғаларын есептеу жазық тригонометрия және алдын ала есептеу формулаларымен орындалады.

Жоғарыда аталған сфералық үшбұрышты есептеудің екі тәсілінен Лежандр тәсілімен есептеудің маңызы зор, себебі тең дәрежелі өлшемді қабырғалары ұзын үшбұрыштарды Лежандр тәсілімен есептеу кезінде қолдануға болады.

Лежандр тәсілімен қабырғалары 550 км болатын сфералық үшбұрыштарды есептеу кезінде эллипсойд бетінің сфералылығын ескеру қажет, демек (25) және (26) формулаларына қосымша мүше енгізу қажет. Сфералық және сфероидтық үшбұрыштарды есептеу теориясы [I] §§20,21 тақыптарында көрсетілген.

№2 Екі меридиан мен параллелдердің ұзындығын есептеу

Меридиандар мен параллелдер доғасының ұзындығын есептеу және кіші сфералық үшбұрыштарды есептеу

1. Ендігі В₁=53°54′30˝+(n·N)˝тең бастапқы пункт пен меридиан доғасы ұзындығын есептеу

n – топтық тізім бойынша студенттің нұсқасы,

N – топтың нөмірі,

n·N – шифрдың соңғы сандары ( сырттай бөлімде оқитын студенттер үшін).

Және ендігі В₂=53°00́12" тең пункт бойынша ,есептеу екі формуламен орындалуы қажет

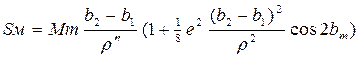
Sм=к·∑·∆В˝, к=8080228·10^-13, ∑=М₁+4Мм+М₂,

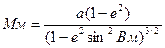Вм=(В₁+В₂)/2,

2. параллелдоғасының ұзындығын ендігі В₁ және бойлықтары әр түрлі болатын ℓ= 1°17^/30" төмендегі формуламен есептеу қажет

Sn=N·cosB(ℓ˝/ρ˝)

3. берілген тапсырманың бірінші пунктінде берілген бастапқы қабырғасы меридиан доғасы болатын триангуляция үшбұрышын есептеу қажет, ал үшбұрыштың сфералық өлшенген бұрыштары ABC сәйкесінше С = 90°ОО'ОО.ОО" А = 41°18'3б,28" В = 48°41́45,5б^” тең болады.

Үшбұрышты есептеу екі тәсілмен орындалады: Лежандр және аддитамент тәсілі бойынша. Сфералық қабырғаларын 1 см дәлдікпен есептеу қажет. Екі тәсілмен есептелген бір атты қабырғаларының ұзындығының айырмашылығы 1 см аспауы тиіс.

4. Берілген тапсырманың 3 пунктінде көрсетілген есептеулер бойынша сфералық қабырғаларымен сфералық үшбұрышты есептеу қажет, демек үшбұрыштың сфералық бұрыштарын есептеу қажет. Сфералық бұрыштардың қосындысы 180° +Е тең болуы қажет.

ҮЛГІ

Тапсырманы есептеу және өңдеу (нөлдік нұсқа)

Бастапқы берілгендері: В₁=53°54́30˝ В₂=53°00́12˝

ℓ=1°17́30° ρ˝=206264,81˝

М₁=6377316,4 м (№1 тапсырмадан)

N₁=6392229.5 м (№1тапсырмадан)

е²=0,006693421 1-е²=0,99330658

а=6378245,0 м

1. Меридиан қисығының радиусын есептеу

В2	53°01’12˝́́́		В1	53°5’׳30˝
Sinb2	́0.7988455		bm	53°27’51°
Sin2 b2	0.6381541		Sin bm	0.8034847
e2 Sin2 b2	0.00427142		Sin 2bm	0.6455876
1- e2 Sin2b2	0.9957285		1- e2 Sin2bm	0.99567883
(1- e2 Sin2 b2)3/2	0.9935997		(1- e2 Sin2bm)3/2	0.9935252
M2	6376362.7 м		Mm	6376840.9 м

М1	6377316,4
4Мм	25507363,6
М2	6376362,7
∑	38261042,7

2. Меридиан доғасының ұзындығын есептеу

В1	53°54'30˝		Мм	6376840.9
В2	53°01'12˝		ρ˝	206264.81˝
∆В	0°53'18˝		S'м=Мм·∆В˝/ρ˝	98868.72 м
∆В˝	5198˝

∑ 38261042,7 е²/8 0.000836678

К 8080228·10^-13 (∆B/ρ)² 0.000240384

∆В 3198˝ cos2Bm -0.2911755

Sм 98898,71 м II -5.8567·10^-8

1-II 0.9999999

Sm_ср=98868,71 м Sm=S´m(1-II) 98898.71 м

3. Паралелдер доғасының үзындығын есептеу

β, 53°54´30» N 6392229,5

ℓ 1⁰17'30» cosВ₁ 0.5890788

N₁ 6392229.5 м ℓ 4650»

r» 206264,81» r 206264,81»

Sn 84889,42 м

4. Лежандр тәсілі бойынша триангуляция үшбұрышын есептеу.

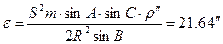
Кесте 1

	Өлшенген сфералық бұрыштар º ´ ˝	Теңестірілген сфералық бұрыштар º ´ ˝	Келтірілген бұрыштар º ´ ˝	Келтірілген бұрыштардың синусы	Сфералық қабырғалары
А	41º18´36,28˝	41º18´36,18˝	41º18´28,97˝	0,6601071	86880,21
В	48º41´45,56˝	48º41´45,46˝	48º41´38,25˝	0,7511945	98868,71
С	90º00´00,00˝	90º00´00,00˝	89º59´52,78˝	1,0000000	131615,32

180000'21,84» 180000'21,64» 180000’00,00”

E. 21,64”

18000’00,20”

W +0,20»

Көрсетілген үлгіде үшбұрыштың қиыспаушылығы тек екі бұрышына ғана таратылған, ал тік бұрышына түзету енгізілмеген. Жалпы жағдайда қиыспаушылық үш бұрышына тең таратылып жазылуы қажет.

1. Аддитамент тәсілі бойынша триангуляция үшбұрышын есептеу.

As_ac=(S³_ac)·409·10^-8=3.96 м

S_ac’ = 98868.71 м – 3.96 м = 98864.75 м

Кесте 2

	Өлшенген сфералық бұрыштары º ´ ˝	Теңестірілген сфералық бұрыштары º ´ ˝	Келтірілген қабырғалары º ´ ˝	Теңестірілген сфералық бұрыштардың синусы	As см	Сфералық қабырғалары
А	48º41´45,56	48º41´45,46˝	98864,75	0,7512176	3,96	98868,71
В	41º18´36,28	41º18´36,18˝	86877,52	,06601334	2,68	86880,21
С	90º00´00,00	90º00´00,00˝	131606,00	1,0000000	9,32	131615,32
	180º00´21,80	180º00´21,64
	E 21,64˝
	180º00´00,2

2. Берілген қабырғалары бойынша трилатерация үшбұрышын есептеу

Бастапқы берілгендер: C= S_AB=131615.32 м r-а=78801,91 м

A=S_AB= 86880,21 м r-b=59813.4I м

B=A_AC = 98868,71 м р-с = 27056,80 м

2р = 317364,24 м бақылау: ρ = 158682,12 м

r = 158682,12 м

I=√p-a=267.95878

II=√p-b=244.56780

III=√p-c=164.5199

IV=√P=398.34924

tg(A´/2)+(II·III / I·IV)=0.3769517 A´/2=20º39´14.49˝ A´=41º18´28.98˝

tg(B´/2)+(I·III / II·IV)=0.4525047 B´/2=24º20´49.13˝ B´=48º41´38.26˝

tg(C´/2)+(I·II / III·IV)=0.9999650 C´/2=44º59´56.39˝ С´=89º59´52.78˝

бақылау: 180º00´00,02˝

Е=a·b·sinC·r˝/(2R²)=21.64˝ Е/3=7.21˝

A=A´+ Е/3=41º18´36.19˝

B=B´+ Е/3=48º41´45.47˝

C=C´+ Е/3=89º59´59.99˝

Берілген тапсырманың 4 және 5 пункттеріне сәйкес теңестірілген сфералық бұрыштар есептелген сфералық бұрыштарға тең болу керек.

Қортынды:

№2 тапсырманы орындау және теориялық бөлімінін оқу кезінде студент меридиандар мен паралельдер доғасының ұзындығын есептеу және кіші сфералық үшбұрыштарды әртүрлі тәсілдермен шешу әдістемесін жақсы меңгерк керек.