Звездные величины

7.1 Прежде всего заметим, что оборот "во сколько раз они слабее" -- это общепринятый жаргон вместо более точного "во сколько раз освещенность от них меньше".

Невооруженным глазом можно видеть звезды до 6-й звездной величины, которые на 22 величины ярче самых слабых звезд, доступных наблюдениям на телескопах Кека. [Кстати, на космическом телескопе им. Хаббла с зеркалом в 2.4 м зарегистрированы объекты . Это потребовало огромных экспозиций. "Обычная" проницающая сила этого телескопа -- 28m].

По определению звездных величин, разности в 5 величин соответствует отношение освещенностей в 100 раз. Поэтому разности в 22 = 5^.4+2 величины соответствует отношение освещенностей . Самые слабые из зарегистрированных к настоящему времени объектов -- звезд и галактик -- почти в миллиард раз слабее звезд, едва различимых невооруженным глазом!

Отношение площадей зеркала телескопа Кека (D=10³ см) и зрачка человеческого глаза (D=0.5 см) составляет 4^.10⁶. Как вы думаете, чем объясняется, что полученное выше отношение предельно малых освещенностей, регистрируемых телескопом Кека и глазом, существенно больше отношения их входных зрачков?

7.2 Разности звездных величин Миры Кита в максимуме и в минимуме блеска соответствует отношение освещенностей, а потому и светимостей в видимом диапазоне, равное .

Однако так как Мира Кита -- холодная красная звезда, большую часть энергии она излучает в ИК-области, и изменения ее интегрального потока гораздо меньше (почему? Указание: см. задачу ). Поэтому болометрическая светимость меняется существенно меньше, чем визуальная.

7.3 Разности в 2.5 звездной величины соответствует отношение освещенностей, равное 10. Но освещенность обратно пропорциональна квадрату расстояния до светила. Так как светимости звезд по условию одинаковы, то одна из них находится в раз дальше другой. [Старомодное слово "светило", использованное в решении задачи, подходит как нельзя лучше. Если тело светится за счет отражения излучения источника, находящегося в месте наблюдения, а не является "истинным светилом", то освещенность от него убывает обратно пропорционально четвертой степени расстояния; см. решения задач и ].

7.4

В настоящее время Плутон находится на расстоянии 30 а.е. от Солнца. Следовательно, освещенность от Солнца на Плутоне в 302 = 900 раз меньше,чем на Земле. Такому отношению освещенностей соответствует разность звездных величин . Так как на Земле видимая звездная величина Солнца равна , то на Плутоне она будет . Это на 6.6 величины меньше, чем видимая звездная величина Луны на Земле . Таким образом, на Плутоне днем более чем в 250 раз светлее, чем в полнолуние на Земле.

7.5 Радиус каждого из миллиона спутников будет в 100 раз меньше радиуса Луны, а площадь поверхности -- в 10000 раз меньше поверхности Луны, так что суммарная поверхность миллиона спутников будет в 100 раз больше поверхности Луны. Следовательно, рой микроспутников будет светить в 100 раз ярче, чем Луна. Отношению освещенностей 1:100 соответствует разность блеска ровно в 5 звездных величин. Поэтому искомая звездная величина m = -12.7-5.0 = -17.7^m.

7.6 Главное при решении этой задачи -- не поддаться искушению сложить звездные величины компонент. Следует помнить, что звездные величины имеют не линейную, а логарифмическую шкалу. Обозначим через и светимости и звездные величины 1-й и 2-й звезды соответственно, а через m -- их суммарную звездную величину. Тогда имеем

и

Мы вправе использовать отношения светимостей звезд вместо отношений освещенностей от них, так как обе компоненты двойной находятся на одном и том же расстоянии от Земли. Из первого равенства находим отношение

и, подставляя его во второе соотношение, получаем

По условию задачи мы имеем , . Поэтому .

Некоторым "эстетическим" недостатком полученной формулы является то, что и входят в нее несимметрично. Попробуйте преобразовать формулу к симметричному виду.

7.7 Очевидно, что освещенность при полном затмении убывает вдвое, а потому звездная величина увеличивается на . Тот факт, что , полезно помнить.

7.8 Равенство звездных величин звезд скопления означает равенство освещенностей, которые они создают на поверхности Земли. Обозначим эту одинаковую для каждой из звезд освещенность через E. Тогда суммарная освещенность, создаваемая всеми N звездами скопления, будет . Из определения звездной величины находим суммарную звездную величину скопления

где m -- звездная величина каждой из составляющих его звезд. В частности, при N=2 имеем (см. предыдущую задачу), при N=10 получаем .

7.9 Обозначим через число звезд ярче звездной величины m, через -- расстояние до слабейших из них (видимая звездная величина m зависит только от расстояния до звезды r, так как светимость всех звезд считается одинаковой). Объем пространства, занятый звездами ярче m-й величины, а следовательно и их число . Освещенность от звезды m-й величины . Отсюда

Переходим здесь от освещенностей к звездным величинам. Поскольку

получаем

Но , так что приближенно

Любопытно, что и при m=0 эта формула дает осмысленный результат. Расхождение с наблюдениями возникает лишь при больших m. Согласно нашей оценке, при увеличении звездной величины на единицу количество звезд возрастает в 4 (точнее, в ) раза. По данным же, полученным прямыми подсчетами, этот показатель меньше: около 3 (см., например, справочник Аллена [1]). Как вы думаете, почему?

Из полученной выше зависимости между и немедленно следует, что

Этот важный результат используется не только в галактической астрономии, но и в радиоастрономии. Терминология и обозначения там, правда, другие. Пусть имеются объекты одинаковой радиосветимости -- внегалактические радиоисточники, и пусть они распределены в пространстве в среднем равномерно. Тогда зависимость числа объектов N, создающих на Земле поток, или освещенность, не менее S, построенная в логарифмических осях, -- так называемая "кривая -- "-- должна представлять собой прямую с угловым коэффициентом -3/2. Подсчеты радиоисточников показывают, что это не так. Причины этого, однако, совсем не те, которые объясняют, почему число звезд (m+1)-й величины превосходит число звезд m-й величины менее чем в 3.98 раза.

Главное, что мы хотели сейчас объяснить -- это то, что коэффициент 3.98, появляющийся при интерпретации звездных подсчетов, и угловой коэффициент 3/2 у радиоастрономической кривой -- -- это по сути дела одно и то же. Связь между числами 3/2 и 3.98, объясняемая различием двух логарифмических шкал, такова: .

7.10 Примем КПД лампочки равным 3%, т.е. будем считать, что лишь 3% потребляемой лампочкой мощности преобразуется в видимый свет. Тогда оптическая светимость лампочки, т.е. энергия, излучаемая ею в видимом диапазоне спектра за 1 с по всем направлениям, будет равна эрг/с. Фотон с длиной волны 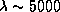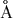имеет энергию эрг. Поэтому фотонная светимость лампочки в видимой части спектра равна . Чтобы лампочка создавала такую же освещенность, как звезда нулевой величины ( 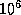фотонов/(см с)), ее следует поместить на расстояние

Отсюда, между прочим, следует, что в большой наземный телескоп 100-ваттную лампочку легко можно было бы заметить, если бы ее включили где-то на орбите Луны (но не на ее поверхности). Она была бы видна как звезда . Хаббловский телескоп смог бы обнаружить ее и на расстоянии в несколько миллионов км!

7.11 Ответ зависит от того, на какую сторону Земли -- дневную или ночную -- мы смотрим. На дневной стороне города различить, конечно, не удастся -- не хватит разрешающей способности глаза (см. задачу ). А вот будут ли ночные города достаточно яркими точками, чтобы их можно было увидеть?

Видимая звездная величина, светимость и расстояние связаны соотношением

Пусть -- видимая звездная величина 100-ваттной лампочки, находящейся на расстоянии 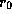; из задачи мы знаем, что при км. Светимость лампочки Вт. Пусть m -- видимая звездная величина крупного города на Земле, наблюдаемого с Луны, т.е. с расстояния км. Будем сначала считать, что его население составляет N = 10 млн. чел., а на каждого человека приходится одна горящая 100-ваттная лампочка. Тогда светимость ночного города была бы Вт. В то же время большая часть лампочек горит в домах, и на долю уличного освещения приходится вряд ли более 10%. Поэтому светимость города будет примерно на порядок меньше, и мы положим Вт. Имеем тогда

Таким образом, ночные города вряд ли видны с Луны невооруженным глазом ("вряд ли" -- учитывая грубость нашей оценки). Но если бы, скажем, в Мехико-сити выпал снег, то появился бы шанс! Может быть, в новоземелии и зимнюю Москву видно с Луны, во всяком случае в бинокль.

7.12 Сравним освещенности от Европы и от Юпитера на поверхности Земли. Оба тела светятся за счет отражения от них излучения Солнца и находятся на одинаковом расстоянии от Земли. Поэтому различие в блеске определяется только разными отражательными свойствами и разными размерами тел.

Обозначим через и альбедо Европы и Юпитера, соответственно. Так как поверхность Европы покрыта льдом, можно считать, что ее альбедо . Для Юпитера примем значение (это значение не дано в условии задачи, но ясно, что если вы возьмете, скажем, 0.5, то ошибка будет не очень велика). Радиусы Европы и Юпитера равны км и км. Имеем:

Звездная величина Юпитера в противостоянии близка к (и вновь эта величина не дана в условии, но вы наверняка видели, что Юпитер в противостоянии заметно ярче Сириуса). Тогда , что незначительно отличается от значения , приводимого в справочнике Аллена [1].

Не удивил ли вас полученный результат? Как вы думаете, почему же мы не видим Европу простым глазом?

7.13 Действительно,

Здесь мы воспользовались приближенным равенством , справедливым при , что следует из замечательного предела

Полученная нами формула, связывающая и , очень полезна. Ее нет ни в одном известном авторам учебнике астрономии, о чем можно только пожалеть.

К планетам эту формулу применять нельзя, точнее, можно применять не всегда (почему?).

7.14 Блеск планеты (орбиту которой мы считаем, естественно, круговой) меняется из-за изменения ее геоцентрического расстояния. Отношение расстояний в противостоянии и в соединении есть

[То, что , находим в уме, учтя, что 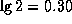]. Но для внешней планеты (у нижних не бывает противостояний!)

где радиус орбиты планеты выражен в а.е. Поэтому

откуда a = 1.5. Это -- Марс.

Впрочем, надеемся, что вы сразу же это сообразили без всякого расчета, едва прочли условие задачи. Всякий, кто интересуется астрономией и хоть немного следил за небом, знает, что ни Юпитер, ни тем более Сатурн так сильно, почти на три с половиной звездных величины, своего блеска не меняют. Расчет подтвердил эту правильную догадку.

7.15 Рассуждая, как в задаче , легко найдем, что большая полуось планеты составляет 5.2 а.е., так что эта планета -- Юпитер. Другой, более простой способ убедиться в этом -- воспользоваться соотношением из задачи , взяв в нем , что дает -- сразу опознается Юпитер.

Сидерический период обращения Юпитера вокруг Солнца P равен приблизительно 12 годам. Синодический период S найдем из уравнения синодического движения

где T -- сидерический период обращения Земли. Синодический период Юпитера в годах равен, таким образом, года, а промежуток времени от соединения до противостояния -- половина синодического периода, т.е. около шести с половиной месяцев.

7.16 Грубая оценка получается мгновенно. Абсолютная звездная величина Солнца примерно +5^m, так что с расстояния в 10 парсеков Солнце будет видно как звезда пятой величины. Предельное расстояние, с которого Солнце еще можно увидеть глазом, должно быть немного больше этого. По формуле из задачи легко найдем (по-прежнему считая абсолютную звездную величину Солнца равной +5^m), что еще на одну звездную величину слабее Солнце станет, если удалиться от него еще на пк. Итак, искомое расстояние близко к 15 пк.

Вот более аккуратный расчет. Абсолютная звездная величина Солнца (в полосе V) равна . Невооруженным глазом видны звезды до 6-й звездной величины. Из известной формулы, связывающей M, m и r, находим

откуда r = 17 пк.

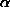7.17 Как известно, Cen -- звезда, по своим физическим характеристикам очень похожая на Солнце. Поэтому можно с уверенностью утверждать, что для наблюдателя, живущего в окрестностях 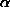Cen, Солнце определенно будет в числе самых ярких звезд -- ведь 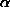Cen входит в число таких звезд для земного наблюдателя. При этом следует также учесть, что Cen -- ближайшая к Солнцу звезда, а все остальные яркие звезды находятся в несколько раз дальше и от Солнца, и от Cen.

7.18 Абсолютная визуальная звездная величина Солнца -- около +5^m. Отсюда

Таким образом, при наблюдении из туманности Андромеды (если не помешает межзвездная пыль) Солнце имело бы звездную величину, примерно равную . Оно было бы недоступно крупнейшим наземным телескопам ( ), но теоретически находилось бы на пределе обнаружимости для хаббловского космического телескопа. Практически же увидеть Солнце было бы невозможно, так как его излучение сливалось бы со светом от тысяч соседних с ним звезд.

7.19 Абсолютная болометрическая звездная величина -- это мера мощности. Пусть M -- искомая абсолютная болометрическая звездная величина пылесоса, а L -- его мощность, которую мы примем равной 800 Вт. Те же величины для Солнца равны и Вт. Тогда

Слабый источник -- пылесос...