Формирователь модулирующих сигналов

Формирователь модулирующих сигналов (ФМС) предназначен для преобразования двоичного цифрового потока от кодера C(t) в модулирующие сигналы I(t) и Q(t), которые необходимо подавать на синфазный и квадратурный входы модулятора для получения заданного сигнального созвездия на его выходе. Он должен содержать:

- регистр сдвига для деления входного потока бит от кодера на группы, передаваемые одним сигналом s_КАМ(t) (дибиты при QPSK и квадбиты при QASK);

- преобразователи уровней битовых сигналов (униполярной кодировки в биполярную: при QPSK «0» → h, «1» → –h; при QASK «00» → 3h, «01» → h, «10» → –h, «11» → –3h);

- дополнительно, при QASK, – кодопреобразователь исходного кода квадбит в код Грея для выравнивания минимальных расстояний между сигналами модулятора и соответствующим им квадбитам.

Требуется:

1. Изобразить сигнальное созвездие для заданного вида модуляции.

а) б)

Рис. 3.4.1. Сигнальные созвездия четырехуровневой QASK (а) и QPSK (б)

а) б)

2. Изобразить график реализации c(t) случайного процесса C(t)

на входе блока ФМС (выходе сверточного кодера) для первых 16 бинарных интервалов (рис. 3.4.2).

Рис. 3.4.2. Осциллограмма реализации с выхода сверточного кодера

Написать аналитическое выражение для случайного процесса .

где ­ прямоугольный импульс длительностью

при

где ­ прямоугольный импульс такой же формы, как , но сдвинутый вправо относительно импульса на величину , если , или влево, если ; - случайная величина 0, +h (значение бита на - интервале ).

3. В соответствии с сигнальным созвездием модулятора QPSK

(или QASK) изобразить для входной реализации графики реализаций и на выходе блока ФМС случайных процессов и на символьных интервалах длительностью T_S (рис. 3.4.3). Написать аналитические выражения для случайных процессов и .

;

где ­ прямоугольный импульс длительностью T_S.

(36)

­ прямоугольный импульс такой же формы, как импульс , но сдвинутый вправо относительно импульса на величину , если , или влево, если ; и ­ независимые случайные величины, заданные на символьном интервале с номером , которые согласно сигнальному созвездию (рис. 3.4.1) принимают:

для QPSK два дискретных значения –h, +h с вероятностью 0,5 каждое, т. е.

;

для QАSK четыре дискретных значения –3h, –h, +h , +3h с вероятностями

для QPSK (вариант 00)

для QАSK (вариант 01)

Рис. 3.4.3. Осциллограммы реализаций i(t) q(t) на выходах и ФМС

4. Написать аналитические выражения для корреляционной функции

и спектральной плотности мощности входного случайного процесса и построить графики этих функций.

Процесс C(t) является случайным синхронным телеграфным сигналом. Его корреляционная функция имеет вид [1]

,

а энергетический спектр

,

где Т = Т_В – длительность тактового интервала.

Графики B_C(τ) и G_C(f) приведены на рис. 3.4.4.

Рис. 3.4.4. Корреляционная функция B_C(τ) (а) и энергетический спектр G_C(f) (б)

синхронного телеграфного сигнала C(t)

5. Написать аналитические выражения для корреляционных функций

B_I(τ) и B_Q(τ), спектральных плотностей мощности G_I(f) и G_Q(f) случайных процессов I(t) и Q(t). Построить графики этих функций.

Процессы I(t) и Q(t) отличаются от процесса C(t) длительностями тактовых интервалов (T_S = 2T_B для QPSK и T_S = 4T_B для QАSK), а для QАSK ещё и начальными значениями B_I(0) = B_Q(0) = D[I(t)] = D[Q(t)] и G_I(0) = G_Q(0) = D[I(t)]/ T_S = D[Q(t)]/ T_S

Графики B_I(τ) и G_I(f) для QАSK приведены на рис. 3.4.5.

Рис. 3.4.5. Корреляционная функция B_I(τ) (а) и

энергетический G_I(f) спектр (б) синхронного телеграфного сигнала I(t)

6. Сравнить графики корреляционных функций и спектральных

плотностей мощности сигналов на входе и выходе блока ФМС. Привести краткое описание результатов сравнения и, используя общие положения теории преобразования Фурье, пояснить, почему спектр выходных сигналов уже спектра входного сигнала.

(Добавить!) 7. Определить длительность символьного интервала T_S.

T_S = 2T_B для QPSK ,

T_S = 4T_B для QPSK,

где T_B - бинарный интервал).

T_S = 2T_B = 2·2,78 = 5,56 мкс (Вар. 0) T_S = 4T_B = 2·1,39 = 5,56 мкс (Вар. 1)

Модулятор

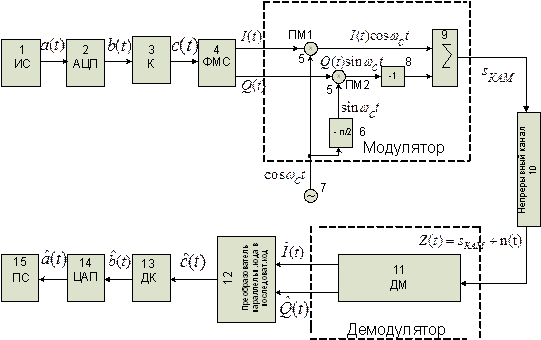
В состав модулятора входят блоки:

- генератор несущего колебания Ucosω_Сt,

- фазовращатель на – для получения квадратурного несущего колебания Usinω_Сt,

- перемножители ПМ 1 и ПМ 2, для получения БМ сигналов S_I(t) = I(t)cosω_Сt и S_Q(t) = Q(t)sinω_Сt, модулированных сигналами I(t) и Q(t), соответственно;

- сумматор для получения сигнала с квадратурной модуляцией

S_КАМ(t) = S_I(t) + S_Q(t) = I(t)cosω_Сt + Q(t)sinω_Сt.

Формулу для определения сигнального созвездия можно представить в следующем виде:

; – фазу отсчитывают по круговому направлению против часовой стрелки, так как в выражении для Q перед А стоит знак минус. Таким образом, при считывании фазы с сигнального созвездия меняем знак по мнимой оси на противоположный (см. знак «минус» перед А в выражении для Q)

Требуется:

Убран п. 1 из методички, пункты 2 и 3 объединены в п. 1.

1. На четырех символьных интервалах T_S нарисовать графики следующих сигналов (в виде символических прямоугольников с указанием их амплитуд и фаз, определенных по сигнальному созвездию заданного вида модуляции):

синфазного БМ сигнала ;

квадратурного БМ сигнала ;

сигнала заданной квадратурной модуляции ;

кодовой последовательности с выхода кодера (без учета их временных сдвигов для удобства сопоставления). Графики указанных сигналов приведены на рис. 3.5.1 – для чётных номеров вариантов – КФМ-4, а для нечётных номеров вариантов – КАМ-16 – на рис 3.5.2.

Рис. 3.5.1. Графики модулированных сигналов s_I(t), s_Q(t) и s_КАМ(t) (для QPSK вар. 02 – КФМ-4)

Рис. 3.5.2. Графики модулированных сигналов s_I(t), s_Q(t) и s_КАМ(t) (для QASK вар. 01– КАМ-16)

2. Написать аналитические выражения для корреляционных функций B_SI(τ), B_SQ(τ) и для спектральных плотностей мощности G_SI(f) и G_SQ(f) сигналов S_I(t) и S_Q(t) (добавить!) на выходах перемножителей модулятора.

Из анализа, приведенного в [2, стр. 41 – 42], следует

,

аналогично

Спектральные плотности мощности G_SI(f) и G_SQ(f) сигналов S_I(t) и S_Q(t) можно найти по теореме Винера-Хинчина как преобразование Фурье от их корреляционных функций [2, стр.43]

,

.

3. Написать аналитические выражения для корреляционной функции сигнала B_S(τ) и для спектральной плотности мощности G_S(f) сигнала S_КАМ(t) заданного вида квадратурной модуляции на выходесумматора модулятора. Построить графики этих функций.

Учитывая, что процесс S_КАМ(t) является суммой двух случайных независимых процессов S_I(t) и S_Q(t)

S_КАМ(t) = S_I(t) + S_Q(t) = I(t)cosω_Сt + Q(t)sinω_Сt,

его корреляционная функция будет равна сумме корреляционных функций слагаемых процессов

B_S(τ) = B_SI(τ) + B_SQ(τ) =

По этой же причине спектральная плотность мощности G_S(f) сигнала S_КАМ(t) есть сумма энергетических спектров G_SI(f) и G_SQ(f) сигналов S_I(t) и S_Q(t), соответственно,

.

Графики B_S(τ) и G_S(f) приведены на рис. 3.5.3.

Рис. 3.5.3. Графики корреляционной функции B_S(τ) и энергетического спектра G_S(f)

4. Определить F_S – ширину спектра модулированного сигнала S_КАМ(t) по второму нулю его огибающей

720 кГц (вариант 0); 720 кГц (вариант 1).

Непрерывный канал

Передача сигнала s_КАМ(t) происходит по непрерывному неискажающему каналу с постоянными параметрами в присутствии

аддитивной помехи типа гауссовского белого шума (АБГШ). Сигнал на выходе такого канала имеет вид

z(t) = μs_КАМ(t) + n(t),

где μ – коэффициент передачи канала. Для всех вариантов принять μ = 1. Односторонняя спектральная плотность мощности помехи равна N_О

(значения N_О для своего варианта взять из таблицы исходных данных).

Требуется:

1. Определить минимально необходимую ширину полосы частот непрерывного канала F_К.

F_К = F_S = 720 кГц (вар. 0); F_К = F_S = 720 кГц (вар. 1)

2. Определить мощность помехи на выходе канала.

Р_П = N_O·F_k = 2,5·10^-7·720·10³ = 0,18 В² (вар. 0, 1)

3. Определить ­ среднюю мощность сигнала s(t) и найти отношение / .

(вар. чётный – КФМ-4)

(вар. нечётный – КАМ-16)

(вар. 0)

(вар. 1)

4. Рассчитать пропускную способность (за секунду) непрерывного канала.

(вар. 0)

5. Оценить эффективность использования пропускной способности непрерывного канала.

где

Демодулятор

Когерентный демодулятор производит анализ принятого приёмником смеси переданного сигнала с помехой z(t) = μs_КАМ(t) + n(t), сопоставляя его с известными образцами сигналов, формируемых модулятором. Анализ завершается принятием решения по критерию максимального правдоподобия в пользу наиболее вероятного передаваемого сигнала (символа).

Требуется:

1. Изобразить структурную схему когерентного демодулятора,

оптимального по критерию максимального правдоподобия для заданного сигнала квадратурной модуляции (рис. 3.7.1).

Рис. 3.7.1. Схема демодулятора для сигнала квадратурной модуляции КАМ-16

2. Написать алгоритмы работы решающих устройств РУ1 и РУ2 в составе когерентного демодулятора.

В момент окончания символьного интервала длительностью решающее устройство (РУ1) сравнивает 4 входных напряжения равенств (77), (80) и выбирает из них максимальное, тем самым реализуя правило принятия решения (76).

Надо:

.

В момент окончания каждого символьного интервала длительностью решающее устройство РУ1 (и РУ2) определяет номер входа , на котором напряжение максимально, и формирует соответствующий дибит в параллельном формате:

«00» при = 1, «10» при = 2, «01» при = 3, «11» при = 4.

3. Определить вероятности ошибок на выходах решающих устройств РУ1 и РУ2 при определении значений символов I_n и Q_n, равных h, –h, 3h, –3h (табл. 3) [2]:

,

,

где P_In=x(ош) и P_Qn=x(ош)­ – вероятности ошибочного приема при In = x и Qn = x, соответственно,

Таблица 3

Передаваемые величины In и Qn	Вероятность ошибки в работе РУ1 и РУ2
In = ±h, Qn = ±h	, где Q (x)– дополнительная функция ошибок, Е1 - энергия сигнала 1·cosωct, Е1 = 0,5·12·TS NO – спектральная плотность мощности БГШ
In = ±3h, Qn = ±3h

=

=

4. Определить вероятности ошибок на выходе преобразователя

параллельного кода в последовательный код (ФМС) для заданных параметров сигналов и [2]:

для точек сигнального созвездия с координатами I_n = ±h, Q_n = ±h (4 точки у QPSK и у QASK)

P_In=h,Qn=h(ош) = P_In=h(ош) + P_Qn=h(ош) – P_In=h(ош)·P_Qn=h(ош),

для точек сигнального созвездия с координатами I_n = ±3h, Q_n = ±3h (4 точки только у QASK)

P_In=3h,Qn=3h(ош) = P_In=3h(ош) + P_Qn=3h(ош) – P_In=3h(ош)·P_Qn=3h(ош),

для точек сигнального созвездия с координатами I_n = ±3h, Q_n = ±h и I_n = ±h, Q_n = ±3h (8 точек только у QASK)

P_In=3h,Qn=h(ош) = P_In=3h(ош) + P_Qn=h(ош) – P_In=3h(ош)·P_Qn=h(ош).

5. Определить среднюю вероятность ошибки на выходе преобразователя:

для QPSK:

P_ср(ош) = 4·P_In=h,Qn=h(ош) / 4 = P_In=h,Qn=h(ош),

для QASK:

P_ср(ош) = [4·P_In=h,Qn=h(ош) + 4· P_In=3h,Qn=3h(ош)+ 8· P_In=3h,Qn=h(ош)] / 16.

Декодер

Декодер формирует из непрерывной последовательности кодовых символов, поступающих с выхода демодулятора (возможно, с ошибками), выходную непрерывную последовательность декодированных кодовых символов, в которых ошибки частично либо полностью исправлены.

Требуется:

1. Изучить алгоритм свёрточного декодирования по методу Витерби [1, с. 253-256].

2. Переписать последовательность кодовых символов, полученных на выходе кодера из п. 4 раздела 3.3

c(iTb) = 110110101001001011.

3. Получить входную для декодера последовательность кодовых символов путём внесения в последовательность b_ВЫХ(k) однократной ошибки в позиции q (по варианту)

â_ВХ(k) = 010110101001001011 (при q = 1).

4. Построить решетчатые диаграммы выживших путей декодера для моментов: t₁ – t₄, t₁ – t₅, t₁ – t₆, t₁ – t₇, t₁ – t₈, t₁ – t₉, t₁ – t₁₀, t₁ – t₄ (рис. 3.8.1). На построенных диаграммах, вычислить метрики путей, входящих в каждый узел диаграммы, выделить фрагменты единственно выживших путей и прочитать по ним декодированную кодовую последовательность â_ВЫХ(k). Убедиться в том, что â_ВЫХ(k) = b_ВЫХ(k), т.е. в исправлении ошибки в позиции q.

Рис. 3.8.1, а. Диаграмма декодера на интервале t₁ – t₄

Рис. 3.8.1, б. Диаграмма декодера на интервале t₁ – t₆

Рис. 3.8.1, в. Диаграмма декодера на интервале t₁ – t₇

Рис. 3.8.1, г. Диаграмма декодера на интервале t₁ – t₈

Рис. 3.8.1, д. Диаграмма декодера на интервале t₁ – t₁₁

ЛИТЕРАТУРА

1. Сальников А.П. Теория электрической связи: Конспект лекций / СПбГУТ. – СПб., 2007. – 273 с.: ил.

2. Общая теория связи: методические указания к выполнению курсовой работы / Л. Н. Куликов, М. Н. Москалец, М. Н. Чесноков. – СПб. : Издательство СПбГУТ, 2012. – 80 с.

ДОПОЛНИТЕЛЬНЫЕ РЕКОМЕНДАЦИИ ПО ОФОРМЛЕНИЮ КР:

Основной текст печатается на одной стороне листа с выравниванием по ширине (Times New Roman, 12 пт, обычный, межстрочный интервал одинарный; абзацный отступ – 1 см).

Поля: верхнее – 2,5 см, нижнее – 3 см, левое – 2,5 см, правое – 2 см.

Не допускается использование табуляции или пробелов для формирования отступа первой строки. Страницы нумеруются.

Рисунки размещаются после ссылок на них, нумеруются внутри разделов и снабжаются подрисуночными надписями. В тексте на них должны быть ссылки.

Для обозначения переменных в формулах и в тексте используют курсив, если буквы из латиницы, и обычный шрифт для кириллицы и греческого алфавита.

При наличии списка литературы, в тексте должны быть ссылки на источники.

Готовая работа сшивается в виде тетради. Использование файликов для вложения листов не допускается.

Сдача КР - 15 неделя

Любые отклонения от исходных данных по варианту рассматриваются как ошибка!

График выполнения КР

Недели	Расчет блоков системы цифровой связи
	Источник сообщений + АЦП
	Кодер + Формирователь модулирующих сигналов
	Модулятор + Непрерывный канал + Демодулятор
	Декодер
	Чистовое оформление и самопроверка КР
	Сдача КР