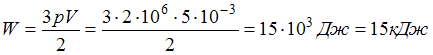Явление электромагнитной индукции
На рисунке показана зависимость силы тока от времени в электрической цепи с индуктивностью 1 мГн:=6
В соответствии с законом Фарадея модуль среднего значения электродвижущей силы самоиндукции равен: 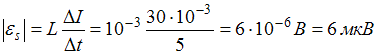 . Изменение тока
. Изменение тока 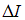 в интервале от 0 до 5 с находится из графика.
в интервале от 0 до 5 с находится из графика.
Сила тока, протекающего в катушке, изменяется по закону 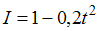 . Если при этом на концах катушки в момент времени
. Если при этом на концах катушки в момент времени 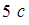 наводится ЭДС самоиндукции величиной
наводится ЭДС самоиндукции величиной 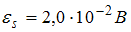 , то индуктивность катушки (в
, то индуктивность катушки (в 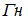 ) равна =0.01
) равна =0.01
ЭДС самоиндукции, возникающая в контуре при изменении в нем силы тока I, определяется по формуле: 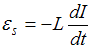 , где L – индуктивность контура. Знак минус в формуле соответствует правилу Ленца: индукционный ток направлен так, что противодействует изменению тока в цепи: замедляет его возрастание или убывание. Таким образом, ЭДС самоиндукции равна
, где L – индуктивность контура. Знак минус в формуле соответствует правилу Ленца: индукционный ток направлен так, что противодействует изменению тока в цепи: замедляет его возрастание или убывание. Таким образом, ЭДС самоиндукции равна 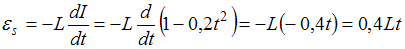
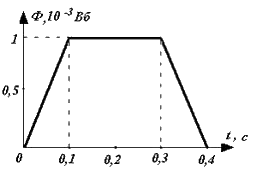
На рисунке представлена зависимость магнитного потока, пронизывающего некоторый контур, от времени:
 ответ
ответ 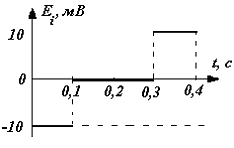
В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: 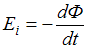 . Следовательно, если магнитный поток увеличивается со временем по линейному закону в интервале 0 – 0,1 с, то ЭДС индукции будет равна отрицательной постоянной величине; если не изменяется в интервале 0,1 – 0,3 с, то ЭДС индукции равна нулю; если убывает по линейному закону в интервале 0,3 – 0,4 с, то ЭДС индукции будет равна положительной постоянной величине.
. Следовательно, если магнитный поток увеличивается со временем по линейному закону в интервале 0 – 0,1 с, то ЭДС индукции будет равна отрицательной постоянной величине; если не изменяется в интервале 0,1 – 0,3 с, то ЭДС индукции равна нулю; если убывает по линейному закону в интервале 0,3 – 0,4 с, то ЭДС индукции будет равна положительной постоянной величине.

Прямоугольная проволочная рамка расположена в одной плоскости с прямолинейным длинным проводником, по которому течет ток I. Индукционный ток в рамке будет направлен по часовой стрелке при ее - поступательном перемещении в отрицательном направлении оси OX
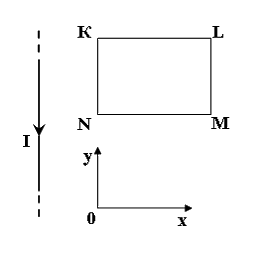
При изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в нем возникает индукционный ток, направление которого можно найти по правилу Ленца, согласно которому индукционный ток имеет такое направление, что его магнитное поле противодействует изменению магнитного потока. В данном случае в прямоугольной проволочной рамке индукционный ток будет протекать по часовой стрелке при ее поступательном перемещении в отрицательном направлении оси OX.
Проводящая рамка вращается с постоянной угловой скоростью в однородном магнитном поле вокруг оси, лежащей в плоскости рамки и перпендикулярной вектору индукции 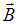 (см. рис.). На рисунке также представлен график зависимости от времени потока вектора магнитной индукции, пронизывающего рамку.
(см. рис.). На рисунке также представлен график зависимости от времени потока вектора магнитной индукции, пронизывающего рамку. 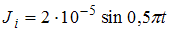
Сила индукционного тока 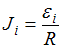 , где
, где 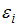 – ЭДС индукции, R – сопротивление рамки. В соответствии с законом Фарадея для электромагнитной индукции
– ЭДС индукции, R – сопротивление рамки. В соответствии с законом Фарадея для электромагнитной индукции 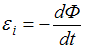 . Чтобы найти закон изменения ЭДС индукции со временем, необходимо знать зависимость от времени магнитного потока, пронизывающего рамку. Из приведенного графика следует, что
. Чтобы найти закон изменения ЭДС индукции со временем, необходимо знать зависимость от времени магнитного потока, пронизывающего рамку. Из приведенного графика следует, что 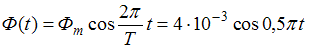 , поскольку
, поскольку 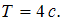 Тогда
Тогда 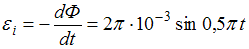 , а
, а 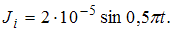
Сила тока в проводящем круговом контуре индуктивностью 100 мГн изменяется с течением времени по закону 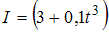 (в единицах СИ):
(в единицах СИ):
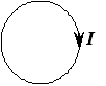
Абсолютная величина ЭДС самоиндукции в момент времени 2 с равна __0,12 В; против часовой стрелки __ ; при этом индукционный ток направлен …
ЭДС самоиндукции, возникающая в контуре при изменении в нем силы тока I, определяется по формуле: 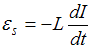 , где L – индуктивность контура. Знак минус в формуле соответствует правилу Ленца: индукционный ток направлен так, что противодействует изменению тока в цепи: замедляет его возрастание или убывание. Таким образом, ЭДС самоиндукции равна
, где L – индуктивность контура. Знак минус в формуле соответствует правилу Ленца: индукционный ток направлен так, что противодействует изменению тока в цепи: замедляет его возрастание или убывание. Таким образом, ЭДС самоиндукции равна 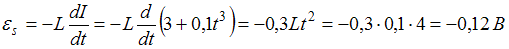 . Абсолютная величина ЭДС самоиндукции равна
. Абсолютная величина ЭДС самоиндукции равна 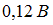 , индукционный ток направлен против часовой стрелки. При этом учтено направление тока в контуре и его возрастание со временем (что следует из заданного закона изменения силы тока).
, индукционный ток направлен против часовой стрелки. При этом учтено направление тока в контуре и его возрастание со временем (что следует из заданного закона изменения силы тока).
Контур площадью 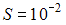 м2 расположен перпендикулярно к линиям магнитной индукции. Магнитная индукция изменяется по закону
м2 расположен перпендикулярно к линиям магнитной индукции. Магнитная индукция изменяется по закону 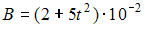
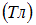 . ЭДС индукции, возникающая в контуре, изменяется по закону …
. ЭДС индукции, возникающая в контуре, изменяется по закону … 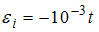
В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: 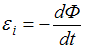 . Поскольку плоскость контура перпендикулярна линиям магнитной индукции,
. Поскольку плоскость контура перпендикулярна линиям магнитной индукции, 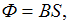 где S – площадь контура. Таким образом,
где S – площадь контура. Таким образом, 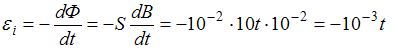
Проводящий плоский контур площадью 75 см2 расположен в магнитном поле перпендикулярно линиям магнитной индукции. Если магнитная индукция изменяется по закону 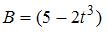 мТл, то ЭДС индукции, возникающая в контуре в момент времени
мТл, то ЭДС индукции, возникающая в контуре в момент времени 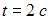 (в мВ), равна =0.18
(в мВ), равна =0.18
В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: 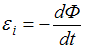 . Поскольку плоскость контура перпендикулярна линиям магнитной индукции,
. Поскольку плоскость контура перпендикулярна линиям магнитной индукции, 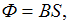 где S – площадь контура. Таким образом,
где S – площадь контура. Таким образом, 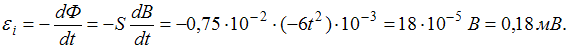
катушка индуктивности и конденсатор соединены последовательно и включены в цепь переменного тока, изменяющегося по закону 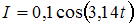 (А). На рисунке представлена фазовая диаграмма падений напряжений на указанных элементах. Амплитудные значения напряжений соответственно равны: на сопротивлении
(А). На рисунке представлена фазовая диаграмма падений напряжений на указанных элементах. Амплитудные значения напряжений соответственно равны: на сопротивлении 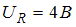 ; на катушке индуктивности
; на катушке индуктивности 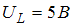 ; на конденсаторе
; на конденсаторе 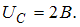
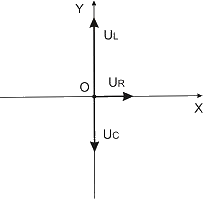
Установите соответствие между сопротивлением и его численным значением.
1. 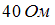 активное сопротивление
активное сопротивление
2. 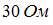 реактивное сопротивление
реактивное сопротивление
3. 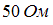 полное сопротивление
полное сопротивление
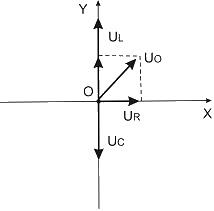
Используем метод векторных диаграмм. Длина вектора равна амплитудному значению напряжения, а угол, который вектор составляет с осью ОХ,
Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными 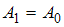 и
и 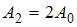 . Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания.
. Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания.
1.0 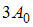
2. 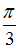
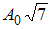
3. 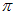
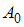
Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле 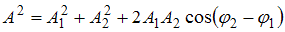 , где
, где 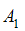 и
и 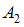 – амплитуды, (
– амплитуды, ( 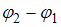 ) – разность фаз складываемых колебаний. Если разность фаз
) – разность фаз складываемых колебаний. Если разность фаз 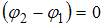 ,
, 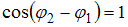 , то
, то 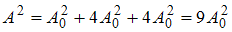 и
и 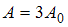 . Этот результат можно было получить сразу: при разности фаз
. Этот результат можно было получить сразу: при разности фаз 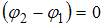 векторы
векторы 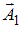 и
и 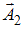 сонаправлены, и длина результирующего вектора
сонаправлены, и длина результирующего вектора 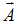 равна сумме длин складываемых векторов. Если
равна сумме длин складываемых векторов. Если 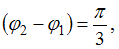
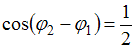 , то
, то 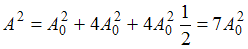 и
и 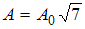 .
.
Если 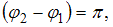
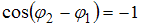 , то
, то 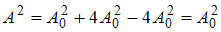 и
и 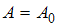 .
.
Сопротивление 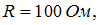 катушка индуктивности
катушка индуктивности 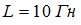 и конденсатор
и конденсатор 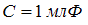 соединены последовательно и подключены к источнику переменного напряжения, изменяющегося по закону
соединены последовательно и подключены к источнику переменного напряжения, изменяющегося по закону 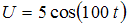 (В). Установите соответствие между сопротивлениями различных элементов цепи и их численными значениями.
(В). Установите соответствие между сопротивлениями различных элементов цепи и их численными значениями.
1.Активноесопротивление 100Ом
2.Индуктивноесопротивление 1000Ом
3. Емкостное сопротивление 10 Ом
Активное сопротивление 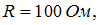 индуктивное сопротивление
индуктивное сопротивление 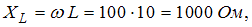 емкостное сопротивление
емкостное сопротивление 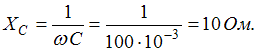
Резистор с сопротивлением 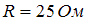 , катушка с индуктивностью
, катушка с индуктивностью 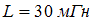 и конденсатор с емкостью
и конденсатор с емкостью 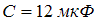 соединены последовательно и подключены к источнику переменного напряжения, изменяющегося по закону
соединены последовательно и подключены к источнику переменного напряжения, изменяющегося по закону 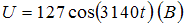 .
.
Установите соответствие между элементом цепи и эффективным значением напряжения на нем.
1.Сопротивление-31В
2.Катушкаиндуктивности-118В
3. Конденсатор-33В
Индуктивное, емкостное и полное сопротивления цепи равны соответственно: 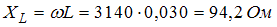 ,
, 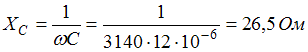 ,
, 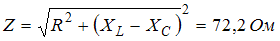 . Максимальное значение тока в цепи
. Максимальное значение тока в цепи 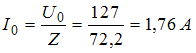 . Эффективное значение тока
. Эффективное значение тока 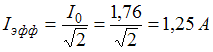 . Тогда искомые падения напряжений на элементах цепи равны:
. Тогда искомые падения напряжений на элементах цепи равны: 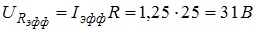 ,
, 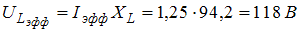 ,
, 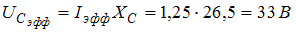 .
.
Складываются два взаимно перпендикулярных колебания. Установите соответствие между номером соответствующей траектории и законами колебаний точки 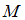 вдоль осей координат
вдоль осей координат 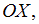
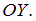
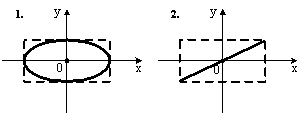
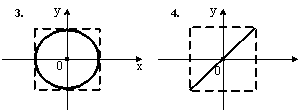
Правильный ответ:
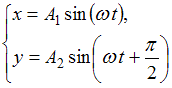 | |||
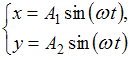 | |||
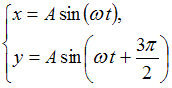 | |||
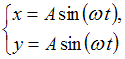 | |||
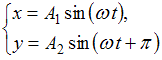 |
При одинаковой частоте складываемых колебаний уравнение траектории точки имеет вид: 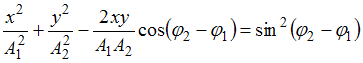 , где
, где 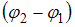 – разность фаз колебаний. Если разность фаз
– разность фаз колебаний. Если разность фаз 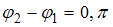 , то уравнение преобразуется к виду
, то уравнение преобразуется к виду 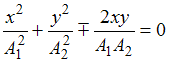 , или
, или 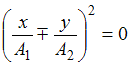 , что соответствует уравнению прямой:
, что соответствует уравнению прямой: 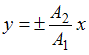 . Если
. Если 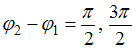 , то
, то 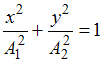 , что является уравнением эллипса, причем если амплитуды равны
, что является уравнением эллипса, причем если амплитуды равны 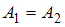 , то это будет уравнение окружности.
, то это будет уравнение окружности.
Если складываются колебания с циклическими частотами 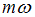 и
и 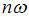 , где
, где 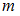 и
и 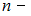 целые числа, точка
целые числа, точка 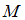 описывает более сложную кривую, которую называют фигурой Лиссажу. Форма кривой Лиссажу зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний.
описывает более сложную кривую, которую называют фигурой Лиссажу. Форма кривой Лиссажу зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний.
Складываются два гармонических колебания одного направления с одинаковыми частотами и амплитудами, равными 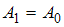 и
и 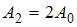 . Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
. Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
1. 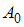
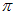
2. 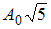
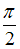
3. 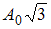
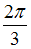
Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле 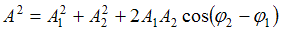 , где
, где 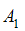 и
и 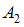 – амплитуды складываемых колебаний, (
– амплитуды складываемых колебаний, ( 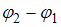 ) – разность их фаз. Если амплитуда результирующего колебания
) – разность их фаз. Если амплитуда результирующего колебания 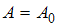 , то
, то 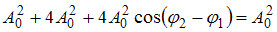 . Тогда
. Тогда 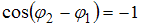 и разность фаз складываемых колебаний равна
и разность фаз складываемых колебаний равна 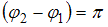 .
.
Если 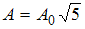 , то
, то 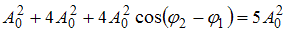 . Тогда
. Тогда 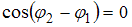 , следовательно,
, следовательно, 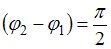 .
.
Если 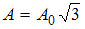 , то
, то 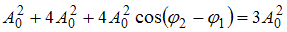 . Тогда
. Тогда 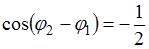 , следовательно,
, следовательно, 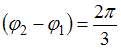 .
.
Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами 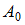 . Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
. Установите соответствие между амплитудой результирующего колебания и разностью фаз складываемых колебаний.
1. 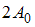 0
0
2. 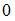
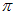
3. 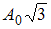
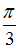
Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле 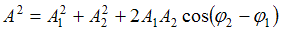 , где
, где 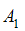 и
и 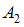 – амплитуды, (
– амплитуды, ( 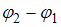 ) – разность фаз складываемых колебаний. Если амплитуда результирующего колебания
) – разность фаз складываемых колебаний. Если амплитуда результирующего колебания 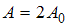 , то
, то 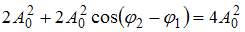 . Тогда
. Тогда 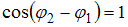 и разность фаз будет равна
и разность фаз будет равна 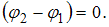
Если 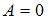 , то
, то 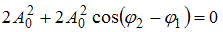 . Тогда
. Тогда 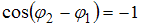 ; следовательно,
; следовательно, 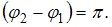
Если 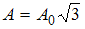 , то
, то 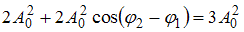 . Тогда
. Тогда 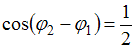 ; следовательно,
; следовательно, 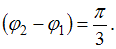
Складываются взаимно перпендикулярные колебания. Установите соответствие между формой траектории и законами колебания точки 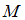 вдоль осей координат
вдоль осей координат 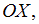
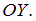
1.Прямаялиния
2.Окружность
3. Фигура Лиссажу
Правильный ответ:
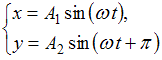 | |||
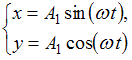 | |||
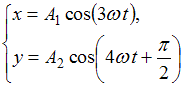 | |||
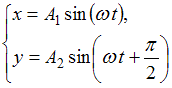 |
При одинаковой частоте колебаний вдоль осей 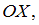
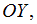 исключив параметр времени, можно получить уравнение траектории:
исключив параметр времени, можно получить уравнение траектории: 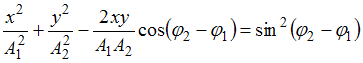 . Если разность фаз колебаний
. Если разность фаз колебаний 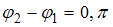 , то уравнение преобразуется к виду
, то уравнение преобразуется к виду 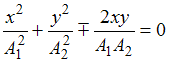 , или
, или 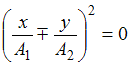 , что соответствует уравнению прямой:
, что соответствует уравнению прямой: 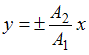 .
.
Если 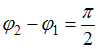 , то
, то 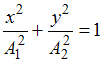 , что является уравнением эллипса, причем если амплитуды равны
, что является уравнением эллипса, причем если амплитуды равны 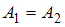 , то это будет уравнение окружности.
, то это будет уравнение окружности.
Если складываются колебания с циклическими частотами 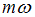 и
и 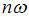 , где
, где 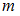 и
и 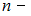 целые числа, точка
целые числа, точка 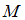 описывает сложную кривую, которую называют фигурой Лиссажу. Форма кривой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний.
описывает сложную кривую, которую называют фигурой Лиссажу. Форма кривой зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний.
Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами 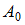 . Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания.
. Установите соответствие между разностью фаз складываемых колебаний и амплитудой результирующего колебания.
1. 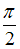
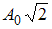
2. 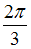
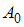
3. 0 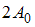
Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле 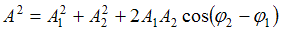 , где
, где 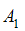 и
и 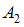 – амплитуды, (
– амплитуды, ( 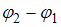 ) – разность фаз складываемых колебаний.
) – разность фаз складываемых колебаний.
Если разность фаз 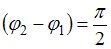 ,
, 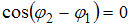 , то
, то 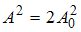 и
и 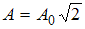 .
.
Если 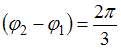 ,
, 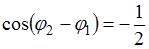 , то
, то 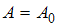 .
.
Если 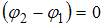 ,
, 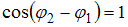 , то
, то 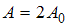 .
.
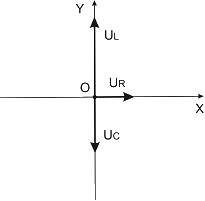
Сопротивление, катушка индуктивности и конденсатор соединены последовательно и включены в цепь переменного тока, изменяющегося по закону 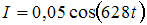 (А). На рисунке схематически представлена фазовая диаграмма падений напряжения на указанных элементах. Амплитудные значения напряжений соответственно равны: на сопротивлении
(А). На рисунке схематически представлена фазовая диаграмма падений напряжения на указанных элементах. Амплитудные значения напряжений соответственно равны: на сопротивлении 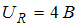 ; на катушке индуктивности
; на катушке индуктивности 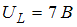 ; на конденсаторе
; на конденсаторе 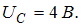
Установите соответствие между сопротивлением и его численным значением.
1.Полноесопротивление=100Ом
2.Активноесопротивление=80Ом
3. Реактивное сопротивление=60Ом
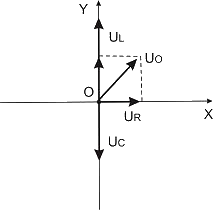
Для решения используется метод векторных диаграмм. Длина вектора равна амплитудному значению напряжения, а угол, который вектор составляет с осью ОХ, равен разности фаз колебаний напряжения на соответствующем элементе и силы тока в цепи. Амплитудное значение полного напряжения равно 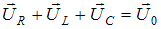 . Величина
. Величина 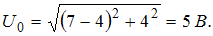 Полное сопротивление цепи связано с амплитудными значениями тока и напряжения законом Ома:
Полное сопротивление цепи связано с амплитудными значениями тока и напряжения законом Ома: 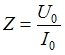 . Амплитудное значение силы тока, как это следует из закона его изменения, равно
. Амплитудное значение силы тока, как это следует из закона его изменения, равно 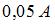 . Тогда
. Тогда 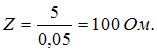 Активное сопротивление
Активное сопротивление 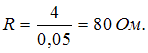 Полное сопротивление цепи равно:
Полное сопротивление цепи равно: 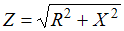 , где
, где 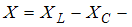 реактивное сопротивление;
реактивное сопротивление; 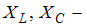 индуктивное и емкостное сопротивления соответственно. Отсюда
индуктивное и емкостное сопротивления соответственно. Отсюда 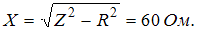
Самая близкая к Земле звезда Проксима Центавра – одна из звезд созвездия Альфа Центавра. Расстояние до нее составляет приблизительно 4,3 световых года. Если бы космический корабль летел от Земли к этой звезде со скоростью 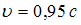 (с – скорость света в вакууме), то путешествие по земным часам и по часам космонавта продлилось бы ____4,5 года и 1,4 года соответственно.
(с – скорость света в вакууме), то путешествие по земным часам и по часам космонавта продлилось бы ____4,5 года и 1,4 года соответственно.
Световой год – внесистемная единица длины, применяемая в астрономии;
1 с.г. равен расстоянию, проходимому светом за один год. Длительность путешествия по часам земного наблюдателя 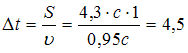 года. Длительность путешествия по часам космонавта (собственное время)
года. Длительность путешествия по часам космонавта (собственное время) 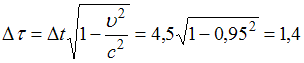 года.
года.
Космический корабль летит со скоростью 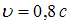 (
( 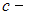 скорость света в вакууме) в системе отсчета, связанной с некоторой планетой. Один из космонавтов медленно поворачивает метровый стержень из положения 1, перпендикулярного направлению движения корабля, в положение 2, параллельное направлению движения. Длина этого стержня с точки зрения другого космонавта - равна 1,0 м при любой его ориентации
скорость света в вакууме) в системе отсчета, связанной с некоторой планетой. Один из космонавтов медленно поворачивает метровый стержень из положения 1, перпендикулярного направлению движения корабля, в положение 2, параллельное направлению движения. Длина этого стержня с точки зрения другого космонавта - равна 1,0 м при любой его ориентации
Движение макроскопических тел со скоростями, соизмеримыми со скоростью света в вакууме, изучается релятивистской механикой. Одним из следствий преобразований Лоренца является так называемое Лоренцево сокращение длины, состоящее в том, что линейные размеры тела сокращаются в направлении движения: 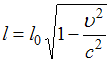 . Здесь
. Здесь 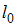 – длина тела в системе отсчета, относительно которой тело неподвижно;
– длина тела в системе отсчета, относительно которой тело неподвижно; 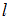 – длина тела в системе отсчета, относительно которой тело движется со скоростью
– длина тела в системе отсчета, относительно которой тело движется со скоростью 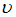 . При этом поперечные размеры тела не изменяются. Поскольку с точки зрения другого космонавта стержень покоится и в положении 1, и в положении 2, то длина стержня равна 1,0 м при любой его ориентации.
. При этом поперечные размеры тела не изменяются. Поскольку с точки зрения другого космонавта стержень покоится и в положении 1, и в положении 2, то длина стержня равна 1,0 м при любой его ориентации.
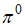 -мезон, двигавшийся со скоростью
-мезон, двигавшийся со скоростью 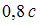 (с – скорость света в вакууме) в лабораторной системе отсчета, распадается на два фотона: g1 и g2. В системе отсчета мезона фотон g1 был испущен вперед, а фотон g2 – назад относительно направления полета мезона. Скорость фотона g1 в лабораторной системе отсчета равна …=1.0с
(с – скорость света в вакууме) в лабораторной системе отсчета, распадается на два фотона: g1 и g2. В системе отсчета мезона фотон g1 был испущен вперед, а фотон g2 – назад относительно направления полета мезона. Скорость фотона g1 в лабораторной системе отсчета равна …=1.0с
Фотон является частицей, которая может существовать, только двигаясь со скоростью с, то есть со скоростью света в вакууме. Кроме того, согласно одному из постулатов специальной теории относительности – принципу постоянства скорости света – скорость света в вакууме не зависит от движения источника света и, следовательно, одинакова во всех инерциальных системах отсчета. Поэтому скорость фотона g1 с учетом направления его движения в лабораторной системе отсчета равна 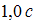 .
.
Предмет движется со скоростью 0,6 с (с – скорость света в вакууме). Тогда его длина для наблюдателя в неподвижной системе отсчета -уменьшится на 20 %
Движение макроскопических тел со скоростями, соизмеримыми со скоростью света в вакууме, изучается релятивистской механикой. Одним из следствий преобразований Лоренца является так называемое лоренцево сокращение длины, состоящее в том, что линейные размеры тела сокращаются в направлении движения: 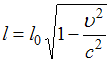 , где
, где 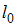 – длина тела в системе отсчета, относительно которой тело неподвижно;
– длина тела в системе отсчета, относительно которой тело неподвижно; 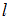 – длина тела в системе отсчета, относительно которой тело движется со скоростью
– длина тела в системе отсчета, относительно которой тело движется со скоростью 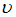 . При этом поперечные размеры тела не изменяются. Относительное изменение длины составит:
. При этом поперечные размеры тела не изменяются. Относительное изменение длины составит: 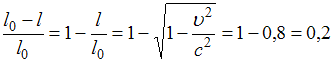 , то есть длина уменьшится на 20%.
, то есть длина уменьшится на 20%.
На борту космического корабля нанесена эмблема в виде геометрической фигуры:
Решение:
Из преобразований Лоренца следует, что линейный размер тела, движущегося относительно инерциальной системы отсчета со скоростью, сравнимой со скоростью света, уменьшается в направлении движения. Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета, поэтому форма тела изменится, как показано на рисунке
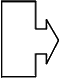
Нестабильная частица движется со скоростью 0,6 с (с – скорость света в вакууме). Тогда время ее жизни в системе отсчета, относительно которой частица движется- увеличится на 25 %.
Из преобразований Лоренца следует, что в движущейся инерциальной системе отсчета со скоростью, сравнимой со скоростью света, наблюдается эффект замедления хода времени. Относительное изменение времени жизни частицы составит:
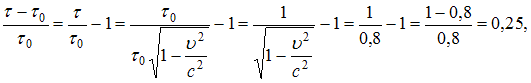
где 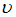 – скорость частицы, с – скорость света,
– скорость частицы, с – скорость света, 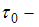 время жизни частицы в системе отсчета, относительно которой частица неподвижна,
время жизни частицы в системе отсчета, относительно которой частица неподвижна, 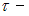 время жизни частицы в системе отсчета, относительно которой частица движется. Следовательно, время жизни частицы увеличится на 25%.
время жизни частицы в системе отсчета, относительно которой частица движется. Следовательно, время жизни частицы увеличится на 25%.
Релятивистское сокращение длины ракеты составляет 20%. При этом скорость ракеты равна =0.6с
Движение макроскопических тел со скоростями, соизмеримыми со скоростью света в вакууме, изучается релятивистской механикой. Одним из следствий преобразований Лоренца является так называемое Лоренцево сокращение длины, состоящее в том, что линейные размеры тела сокращаются в направлении движения: 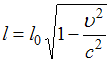 . Здесь
. Здесь 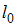 – длина тела в системе отсчета, относительно которой тело неподвижно;
– длина тела в системе отсчета, относительно которой тело неподвижно; 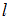 – длина тела в системе отсчета, относительно которой тело движется со скоростью
– длина тела в системе отсчета, относительно которой тело движется со скоростью 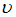 . При этом поперечные размеры тела не изменяются. По условию релятивистское сокращение длины ракеты
. При этом поперечные размеры тела не изменяются. По условию релятивистское сокращение длины ракеты 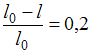 .
. 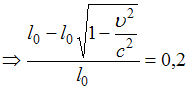 . Отсюда скорость ракеты
. Отсюда скорость ракеты 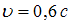 .
.
Частица движется со скоростью 0,8 с (с – скорость света в вакууме). Тогда ее масса по сравнению с массой покоя- увеличится на 67 %.
Зависимость релятивистской массы частицы от ее скорости определяется по формуле: 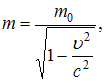 где
где 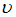 – скорость частицы, с – скорость света,
– скорость частицы, с – скорость света, 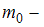 масса покоя частицы, m – релятивистская масса частицы. Относительное изменение массы частицы составит:
масса покоя частицы, m – релятивистская масса частицы. Относительное изменение массы частицы составит:
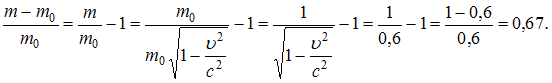
Следовательно, масса частицы увеличится на 67%.
Потенциальная энергия частицы задается функцией 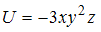 .
.
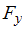 -компонента (в Н) вектора силы, действующей на частицу в точке А (3, 1, 2), равна =36
-компонента (в Н) вектора силы, действующей на частицу в точке А (3, 1, 2), равна =36
(Функция 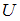 и координаты точки А заданы в единицах СИ.)
и координаты точки А заданы в единицах СИ.)
Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид 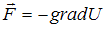 , или
, или 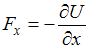 ,
, 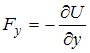 ,
, 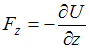 . Таким образом,
. Таким образом, 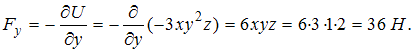
Тело движется под действием силы, зависимость проекции которой от координаты представлена на графике:
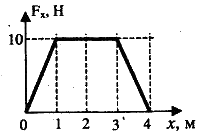
Работа силы (в 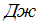 ) на пути 4 м равна =30
) на пути 4 м равна =30
Работа переменной силы на участке 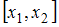 определяется как интеграл:
определяется как интеграл: 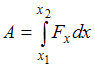 . Используя геометрический смысл определенного интеграла, можно найти работу, которая численно равна площади трапеции
. Используя геометрический смысл определенного интеграла, можно найти работу, которая численно равна площади трапеции 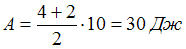 .
.
Для того чтобы раскрутить стержень массы 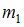 и длины
и длины 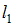 (см. рисунок) вокруг вертикальной оси, проходящей перпендикулярно стержню через его середину, до угловой скорости
(см. рисунок) вокруг вертикальной оси, проходящей перпендикулярно стержню через его середину, до угловой скорости 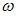 , необходимо совершить работу
, необходимо совершить работу 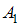 .
.
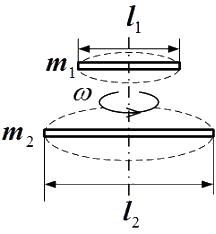
Для того чтобы раскрутить до той же угловой скорости стержень массы 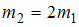 и длины
и длины 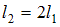 , необходимо совершить работу в- 8 раз(-а) б
, необходимо совершить работу в- 8 раз(-а) б
Совершенная работа равна кинетической энергии вращательного движения стержня 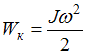 , где момент инерции стержня
, где момент инерции стержня 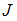 пропорционален массе и квадрату длины,
пропорционален массе и квадрату длины, 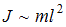 (момент инерции стержня массы
(момент инерции стержня массы 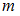 и длины
и длины 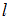 относительно оси, проходящей перпендикулярно ему через середину стержня, равен
относительно оси, проходящей перпендикулярно ему через середину стержня, равен 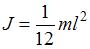 ). Следовательно, работа по раскручиванию до такой же угловой скорости
). Следовательно, работа по раскручиванию до такой же угловой скорости 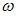 стержня вдвое б
стержня вдвое б
На рисунке показан вектор силы, действующей на частицу: 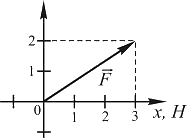
Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (3; 2), равна 19_ 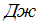 .
.
По определению 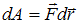 . С учетом того, что
. С учетом того, что 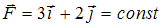 (см. рис.),
(см. рис.), 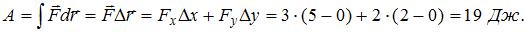
Потенциальная энергия частицы задается функцией 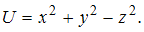
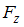 -компонента (в Н) вектора силы, действующей на частицу в точке А (1, 2, 3), равна =6
-компонента (в Н) вектора силы, действующей на частицу в точке А (1, 2, 3), равна =6
(Функция 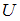 и координаты точки А и заданы в единицах СИ.)
и координаты точки А и заданы в единицах СИ.)
Связь между потенциальной энергией частицы и соответствующей ей потенциальной силой имеет вид: 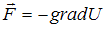 , или
, или 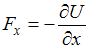 ,
, 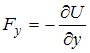 ,
, 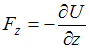 . Таким образом,
. Таким образом, 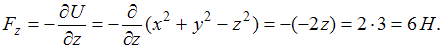
Материальная точка массой 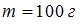 начинает двигаться под действием силы
начинает двигаться под действием силы 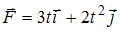 (Н) . Если зависимость радиуса-вектора материальной точки от времени имеет вид
(Н) . Если зависимость радиуса-вектора материальной точки от времени имеет вид 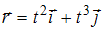 (м), то мощность (Вт), развиваемая силой в момент времени
(м), то мощность (Вт), развиваемая силой в момент времени 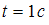 равна =12
равна =12
Мощность, развиваемая силой в некоторый момент времени, равна: 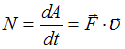 , где
, где 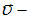 скорость материальной точки, равная:
скорость материальной точки, равная: 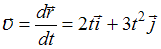 . Следовательно,
. Следовательно, 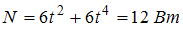 .
.
На концах невесомого стержня длины l закреплены два маленьких массивных шарика. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости 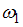 . Под действием трения стержень остановился, при этом выделилось 4 Дж теплоты.
. Под действием трения стержень остановился, при этом выделилось 4 Дж теплоты.
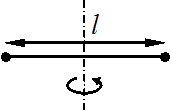
Если стержень раскрутить до угловой скорости 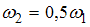 , то при остановке стержня выделится количество теплоты (в Дж), равное =1
, то при остановке стержня выделится количество теплоты (в Дж), равное =1
Согласно закону сохранения энергии количество выделившейся теплоты равно убыли полной механической энергии, в данном случае – убыли кинетической энергии вращения: 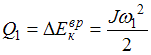 . Отсюда следует, что при уменьшении угловой скорости в 2 раза количество выделившейся теплоты уменьшится в 4 раза, то есть
. Отсюда следует, что при уменьшении угловой скорости в 2 раза количество выделившейся теплоты уменьшится в 4 раза, то есть 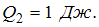
При комнатной температуре отношение 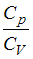 молярных теплоемкостей при постоянном давлении и постоянном объеме равно
молярных теплоемкостей при постоянном давлении и постоянном объеме равно 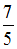 для- кислорода
для- кислорода
Из отношения 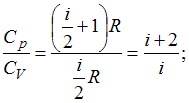
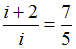 найдем
найдем 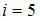 ,
, 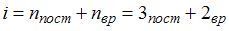 . Так как 3 поступательные и 2 вращательные степени свободы имеют двухатомные газы, следовательно, это кислород.
. Так как 3 поступательные и 2 вращательные степени свободы имеют двухатомные газы, следовательно, это кислород.
Средняя кинетическая энергия молекул газа при температуре 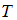 зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекулы водяного пара (
зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное и вращательное движение молекулы как целого, средняя кинетическая энергия молекулы водяного пара ( 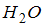 ) равна 3 kT
) равна 3 kT
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная 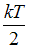 , а на каждую колебательную степень –
, а на каждую колебательную степень – 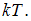 Средняя кинетическая энергия молекулы равна:
Средняя кинетическая энергия молекулы равна: 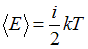 . Здесь
. Здесь 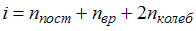 , где
, где 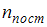 – число степеней свободы поступательного движения,
– число степеней свободы поступательного движения, 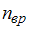 – число степеней свободы вращательного движения,
– число степеней свободы вращательного движения, 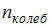 – число степеней свободы колебательного движения. Для молекул идеального газа
– число степеней свободы колебательного движения. Для молекул идеального газа 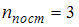 ,
, 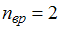 для линейных молекул и
для линейных молекул и 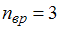 для нелинейных молекул. Молекула водяного пара является нелинейной, поэтому для нее
для нелинейных молекул. Молекула водяного пара является нелинейной, поэтому для нее 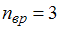 . Поскольку по условию имеет место поступательное и вращательное движение молекулы как целого,
. Поскольку по условию имеет место поступательное и вращательное движение молекулы как целого, 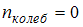 . Таким образом,
. Таким образом, 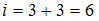 . Тогда средняя энергия молекулы водяного пара (
. Тогда средняя энергия молекулы водяного пара ( 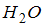 ) равна:
) равна: 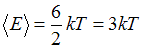 .
.
При комнатной температуре коэффициент Пуассона 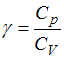 , где
, где 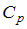 и
и 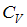 – молярные теплоемкости при постоянном давлении и постоянном объеме соответственно, равен
– молярные теплоемкости при постоянном давлении и постоянном объеме соответственно, равен 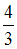 для - водяного пара
для - водяного пара
Из отношения 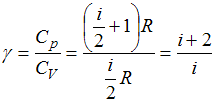 . При комнатной температуре
. При комнатной температуре 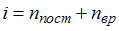 , где
, где 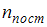 и
и 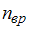 – число поступательных и вращательных степеней свободы. По условию
– число поступательных и вращательных степеней свободы. По условию 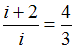 . Отсюда
. Отсюда 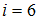 . Так как для молекул газа
. Так как для молекул газа 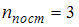 , то для рассматриваемого газа
, то для рассматриваемого газа 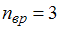 , а три вращательные степени свободы имеют трехатомные и многоатомные газы с нелинейными молекулами. Следовательно, речь идет о водяном паре.
, а три вращательные степени свободы имеют трехатомные и многоатомные газы с нелинейными молекулами. Следовательно, речь идет о водяном паре.
Если не учитывать колебательные движения в молекуле водорода при температуре 200 К, то кинетическая энергия в (Дж) всех молекул в 4 г водорода равна =8310
Средняя кинетическая энергия одной молекулы равна: 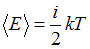 , где
, где 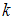 – постоянная Больцмана,
– постоянная Больцмана, 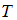 – термодинамическая температура;
– термодинамическая температура; 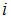 – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы
– сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы 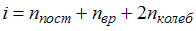 . Молекула водорода
. Молекула водорода 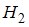 имеет 3 поступательные и 2 вращательные степени свободы, следовательно,
имеет 3 поступательные и 2 вращательные степени свободы, следовательно, 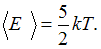 В 4 г водорода содержится
В 4 г водорода содержится 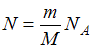 молекул, где
молекул, где 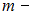 масса газа,
масса газа, 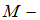 молярная масса водорода,
молярная масса водорода, 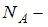 число Авогадро. Кинетическая энергия всех молекул будет равна:
число Авогадро. Кинетическая энергия всех молекул будет равна: 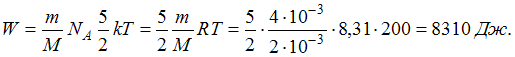
Средняя кинетическая энергия молекул газа при температуре 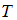 зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, отношение средней кинетической энергии колебательного движения к полной кинетической энергии молекулы азота (
зависит от их конфигурации и структуры, что связано с возможностью различных видов движения атомов в молекуле и самой молекулы. При условии, что имеет место поступательное, вращательное движение молекулы как целого и колебательное движение атомов в молекуле, отношение средней кинетической энергии колебательного движения к полной кинетической энергии молекулы азота ( 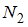 ) равно 2/7
) равно 2/7
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная 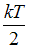 , а на каждую колебательную степень –
, а на каждую колебательную степень – 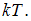 Средняя кинетическая энергия молекулы равна:
Средняя кинетическая энергия молекулы равна: 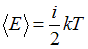 . Здесь
. Здесь 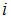 – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: 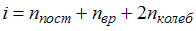 , где
, где 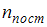 – число степеней свободы поступательного движения, равное 3;
– число степеней свободы поступательного движения, равное 3; 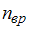 – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;
– число степеней свободы вращательного движения, которое может быть равно 0, 2, 3; 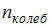 – число степеней свободы колебательного движения, минимальное количество которых равно 1.
– число степеней свободы колебательного движения, минимальное количество которых равно 1.
Для молекулярного азота (двухатомной молекулы) 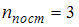 ,
, 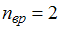 и
и 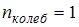 . Следовательно,
. Следовательно, 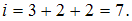 Полная средняя кинетическая энергия молекулы азота (
Полная средняя кинетическая энергия молекулы азота ( 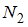 ) равна:
) равна: 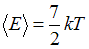 , энергия колебательного движения
, энергия колебательного движения 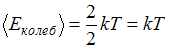 , тогда отношение
, тогда отношение 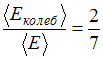 .
.
В соответствии с законом равномерного распределения энергии по степеням свободы средняя кинетическая энергия молекулы идеального газа при температуре T равна: 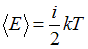 . Здесь
. Здесь 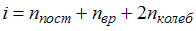 , где
, где 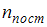 ,
, 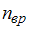 и
и 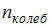 – число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для водорода (
– число степеней свободы поступательного, вращательного и колебательного движений молекулы соответственно. Для водорода ( 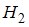 ) число i равно=7
) число i равно=7
Для статистической системы в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная 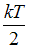 , а на каждую колебательную степень –
, а на каждую колебательную степень – 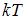 . Средняя кинетическая энергия молекулы равна:
. Средняя кинетическая энергия молекулы равна: 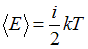 . Здесь
. Здесь 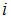 – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:
– сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: 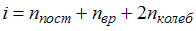 , где
, где 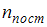 – число степеней свободы поступательного движения, равное 3;
– число степеней свободы поступательного движения, равное 3; 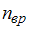 – число степеней свободы вращательного движения, которое может быть равно 0, 2, 3;
– число степеней свободы вращательного движения, которое может быть равно 0, 2, 3; 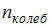 – число степеней свободы колебательного движения, минимальное количество которых равно 1.
– число степеней свободы колебательного движения, минимальное количество которых равно 1.
Для водорода ( 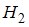 ) (двухатомной молекулы)
) (двухатомной молекулы) 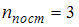 ,
, 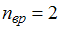 и
и 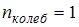 . Следовательно,
. Следовательно, 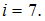
Молярная теплоемкость идеального газа при постоянном давлении равна 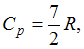 где
где 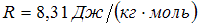 – универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно =2
– универсальная газовая постоянная. Число вращательных степеней свободы молекулы равно =2
Молярная теплоемкость идеального газа в изобарном процессе определяется соотношением 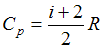 , где
, где 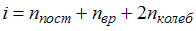 . Здесь
. Здесь 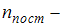 число степеней свободы поступательного движения;
число степеней свободы поступательного движения; 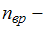 число степеней свободы вращательного движения;
число степеней свободы вращательного движения; 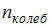 – число степеней свободы колебательного движения. Для молекул идеального газа
– число степеней свободы колебательного движения. Для молекул идеального газа 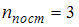 ,
, 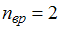 для линейных молекул и
для линейных молекул и 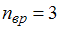 для нелинейных молекул. Из сопоставления с данными задания следует, что
для нелинейных молекул. Из сопоставления с данными задания следует, что 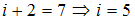 . С учетом того что
. С учетом того что 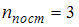 , приходим к выводу, что
, приходим к выводу, что 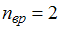 . В данном случае
. В данном случае 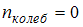 .
.
Газ занимает объем 5 л под давлением 2 МПа. При этом кинетическая энергия поступательного движения всех его молекул равна =15 кДж
Согласно уравнению кинетической теории для давления идеального газа (основному уравнению МКТ идеальных газов), произведение давления идеального газа и его объема равно двум третям энергии поступательного движения всех его молекул: 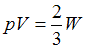 . Отсюда
. Отсюда