Признак параллельности прямой и плоскости

Теорема: Для того, чтобы прямая была параллельна плоскости, необходимо и достаточно, чтобы прямая была параллельна некоторой прямой, принадлежащей плоскости.

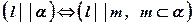
1. Необходимый признак: Если прямая параллельна плоскости, то она параллельна некоторой прямой, принадлежащей плоскости.

Дано: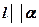

Доказать: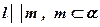

Доказательство:

Выберем на плоскости a произвольную точку М: МÎa .

Через прямую l и непринадлежащую ей точку М проведем плоскость b: l Ì b , МÎb .

Плоскости a и b пересекаются по прямой т, проходящей через их общую точку М (аксиома I₅).

Согласно вспомогательной теореме прямая l, принадлежащая плоскости b и параллельная плоскости a, будет параллельна прямой пересечения плоскостей a и b, то есть .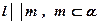

2. Достаточный признак: Если прямая параллельна некоторой прямой, принадлежащей плоскости, то она параллельна плоскости.

Дано: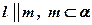

Доказать: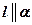

Доказательство:

Через параллельные прямые l и т проведем плоскость b. Плоскости a и b пересекаются: , так как т Ì a и т Ì b.

Предположим, что прямая l пересекает плоскость a: . Следовательно, точка М принадлежит прямой пересечения плоскостей a и b: М Î т.

А значит, 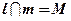, что противоречит условию .Получили противоречие с условием теоремы, следовательно, предположение не верно. А значит, .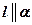

Вывод: Чтобы доказать, что данная прямая параллельна данной плоскости, надо назвать (найти) в этой плоскости прямую, параллельную данной прямой.

Упражнения:

Сторона АВ треугольника АВС лежит в плоскости a. Как расположена относительно этой плоскости прямая MN, проходящая через середины сторон АС и ВС?

Через сторону АВ правильного шестиугольника ABCDEF проведена плоскость a. Как расположены по отношению к этой плоскости прямые: СF, CD, DF, DE?

5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ

ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ДВУХ ПЛОСКОСТЕЙ

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ

I₄. Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость.

Вывод: Плоскости, имеющие три различные общие точки, совпадают.

I₅. Если две различные плоскости имеют общую точку, то их пересечением является прямая.

Вывод: Две плоскости либо пересекаются по прямой, либо не пересекаются, то есть не имеют ни одной общей точки.

В пространстве рассматриваются три случая возможного расположения двух плоскостей:

1. Плоскости совпадают. Рис. 1. a = АВС;

2. Плоскости пересекаются. Рис. 2. a ìüb = l;

3. Плоскости не имеют общих точек. Рис. 3. a ìüb = Æ.

Рис. 1. Рис. 2. Рис. 3.

Определение: Плоскости параллельны, если они не имеют общих точек или совпадают.