Проекции с числовыми отметками
Б2.Б.3 Инженерная графика
Методические указания
к выполнению контрольной работы №2 по инженерной графике
Направление 270800 – Строительство
.
.
Уфа 2012
УДК 514
ББК 22.15
Н 36
Рекомендовано к изданию методической комиссией факультета землеустройства и лесного хозяйства (протокол № 3 от 10 ноября 2012 г.)
Составители: доцент Тархова Л.М.
Рецензент: д.т.н., профессор
кафедры природообустройства
строительства и гидравлики А.Р.Хафизов
Ответственный за выпуск: заведующий кафедрой «Начертательная геометрия и графика» доцент Тархова Л.М.
ФГБОУ ВПО «Башкирский ГАУ», кафедра Начертательной геометрии и графики, тираж 50 экз.
Введение
Изучение дисциплины «Инженерная графика» необходимо для приобретения знаний, умений и навыков, позволяющих составлять и читать технические чертежи, проектную документацию. Дисциплина «Инженерная графика состоит из двух курсов. В курсе «Начертательная геометрия» изучается метод проецирования, с помощью которого развивается инженерно-пространственное воображение. Практическое использование полученных знаний рассматривается в курсе «Черчение». Знания по построению изображений, решению задач, правила составления и оформления чертежа находят широкое применение при разработке проектов и в строительстве сооружений.
Задача контрольной работы научить построению изображения пространственных форм на плоскости, разобрать различные способы решения задач геометрического характера, а также научить студентов правильно читать и выполнять строительные чертежи. Знания и навыки, приобретенные при изучении дисциплины, необходимы при изучении специальных курсов и дальнейшей деятельности. Вся последовательность графических построений подробно описана в указаниях к выполнению конкретного задания.
Цель данных методических указаний – активизация, интенсификация и совершенствование самостоятельной работы студентов.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа представляет собой эпюры (чертежи), которые выполняются по мере последовательности прохождения курса.
Задачи на контрольные работы индивидуальные. Они представлены в вариантах. Студент выполняет тот вариант задания, номер которого соответствует сумме трех последних цифр его шифра. Если, например, учебный шифр 7136, то он во всех задачах выполняет седьмой вариант (1+3+6=10).
Контрольная работа представляется на рецензию в полном объеме. представление ее по частям (отдельные эпюры) не разрешается.
Если работа не зачтена, преподаватель в рецензии указывает какую часть контрольной работы надо переделать или же выполнить всю контрольную работу вновь. На повторную рецензию следует высылать всю контрольную работу полностью.
Эпюры контрольной работы выполняются на листах чертежной бумаги формата А3 по ГОСТ 2.301-68. все надписи, как и отдельные обозначения, в виде букв и цифр на эпюре должны быть выполнены стандартным шрифтом размером 3,5 или 5 в соответствии с ГОСТ 2.304-81
Задача 1 лист1
ТЕНИ ЗДАНИЯ
Даны ортогональные проекции здания. (Приложение А)
Требуется построить тени здания в ортогональных проекциях.
Для выполнения задания рассмотреть пример в учебнике [6, с. 235, с. 245, рис. 604 – 605; 7, с. 151 – 156, рис. 322 – 330].
Чертеж задачи выполняется на листе чертежной бумаги формата А3, расположенном вертикально, в масштабе 1:1. Данные для выполнения эпюра находятся в приложении А.
Чаще всего построение теней в ортогональных проекциях осуществляется при параллельных световых лучах. При этом за направление лучей света обычно принимают направление диагонали куба, две грани которого совмещены с плоскостями проекций (рисунок 1).
При построении теней следует учитывать следующие положения.
Тенью от точки на плоскость является след светового луча на эту плоскость. Тень от прямой параллельной плоскости проекции на эту плоскость равна и параллельна самому отрезку. Тень от прямой перпендикулярной плоскости проекций совпадает с проекцией луча на эту плоскость.
Проекциями диагонали куба являются соответствующие диагонали квадрата, т. е. каждая из проекций светового луча S(S1, S2) составляет с осью x12 угол 45°.
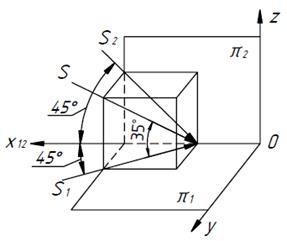 Рисунок 1 Направление лучей света Рисунок 1 Направление лучей света | Алгоритм решения задачи следующий (рисунок 2): 1. Перечерчиваем горизонтальную и фронтальную проекции здания (между ними оставляем расстояние равное ≈ 1,2 максимальной высоты здания). Размеры не проставляем. 2. Определяем поверхности, находящиеся в собственной тени. 3. Строим падающие тени от элементов здания на землю π1 (рисунок 2). Контур падающей тени является тенью контура собственной. |
Для построения контура падающей тени от крыши на землю ( π1) проводим фронтальные проекции световых лучей через точки 1, 2, 3, 5 до земли (ось x12). Затем из точек пересечения этих лучей с землей проводим линии связи. В пересечении линий связи с горизонтальными проекциями световых лучей, идущих через данные точки, получаем 11t, 21t, 31t и 51t.Конек 5 – 12 параллелен земле. Следовательно, тень от конька на плоскость π1 равна и параллельна отрезку 5 – 12. Проводим через 51t линию, параллельную 51 – 121. Эта линия пересечет тень от линии слива 3 – 4 в точке 25. Углы дома 17, 17' и 19, 19' перпендикулярны земле, значит тени от них пойдут под углом 45° к оси x12. Тень от участка слива 1 – 14 на землю пойдет параллельно до угла 17, 17'. Тень от карниза 7 – 8 на землю строим полностью и ограничиваем тенью от угла дома 19, 19'.
4. Построим тени от конька 5 – 12 на фасад и крышу здания. Конек 5 - 12 перпендикулярен к плоскости π2 и, следовательно, по π2 тень совпадает с проекцией луча на π2 При нахождении тени от конька 5 – 12 на задний скат крыши применяем. способ обратного луча.
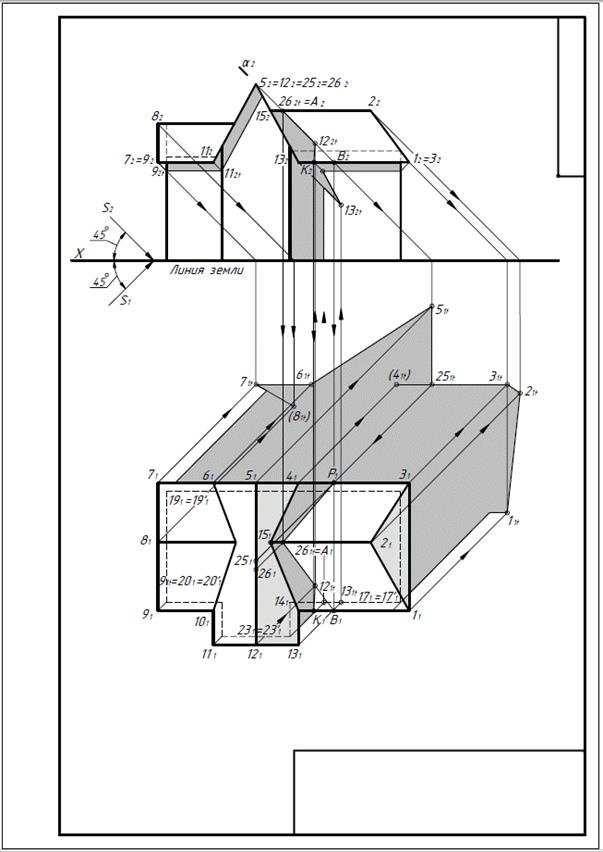 |
| Рисунок 2 Падающие тени от элементов здания на землю |
Из точки 251t проводим линию параллельно световым лучам, но в обратном направлении, и на линии слива 3 – 4 находим точку P, в которой тень от конька делится на два участка. Один из них 5 – 25 дает тень на землю, другой 25 – 26 на крышу. Тень от точки 26 находим проведением светового луча из точки 26, до конька 2 – 15. Участок 12 – 26 даст тень на ближайший скат крыши. Тень от точки 12 находим как точку пересечения светового луча, проведенного через точку 12, с плоскостью ската. Для этого световой луч заключаем во фронтально проецирующую плоскость α(α2) и определяем линию пересечения этой плоскости со скатом (AB). 121t получаем в пересечении A1B1 и горизонтальной проекции луча, идущего через 12.
Точки 9, 10, 14 и 1 принадлежат одной линии слива, параллельной стене здания. Найдя тень от точки 9, попавшую на ребро здания 20, 20', определяем тень от всего слива на стену. Так же определяем тень от карниза 11 – 12 на стену пристройки. Построим тень от пристройки на фасад здания. Из горизонтальной проекции точки 131 проводим световой луч S1 до стены и по линии связи определим фронтальную проекцию тени точки 13(131t, и 132t) на фасаде здания.
Так как карниз 12 – 13 параллелен стене, то тень от него на стену пойдет параллельно самому карнизу до пересечения с тенью от линии слива 1 – 14. Из общей точки пересечения этих теней проводим обратный луч до линии слива 1 – 14 и получаем участок тени от карниза 12 – 13 на скат крыши (12 – K). Линия слива 13 – 14 перпендикулярна стене здания – значит, тень от нее на стену совпадет с проекцией луча из 13t. Угол стены пристройки 23, 23' параллелен стене здания, следовательно, тень от него на стену будет параллельна самому углу. Из горизонтальной проекции угла 23, 23' проводим световой луч до стены и по линии связи определяем фронтальную проекцию тени. Продолжаем ее до пересечения с тенью от слива 13 – 14.
5. Построим тени от трубы на скат крыши (рисунок 3). Определяем все тенеобразующие ребра трубы (ребра с основаниями A, B, C на скате крыши). Построим тень от точки 1. Проводим проекции светового луча через точку 1. Заключаем луч в горизонтально проецирующую плоскость α (след α1), которая пересечет скат крыши по линии MN. Пересечение M2N2 с проекцией светового луча S2, проходящим через точку 12, даст тень от точки 1 (12t) на скате крыши. По линии связи находим горизонтальную проекцию тени от точки 1 (11t).
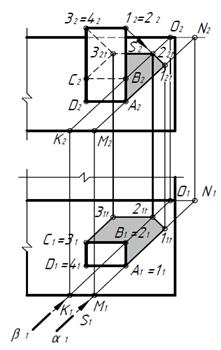 Рисунок 3 Построение тени от трубы Рисунок 3 Построение тени от трубы | Аналогично построим тень от точки 2 (21t,22t) и соединим прямой точки 11t и 21t, 12t и 12t.[1t, 2t] – тень от горизонтального ребра [1, 2] на скате крыши; соединив 1t с A (11t – A1; 12t –A2), получим тень от ребра 1 – A. Построим тень (3t – 2t) от горизонтального ребра 3 – 2. Тень (3t – 2t) параллельна ребру 3 – 2. Проводим тень Ct– 3t от вертикального ребра C – 3 (Ct– 3t должна быть параллельна MN и KO). 6. После выполнения построений производим отмывку эпюра разведенной черной тушью или раствором черной акварельной краски. Все изображения отмываем 1 раз, собственные тени – 2 |
раза, падающие – 3 раза.
Линии построения контуров теней и характерных точек сохраняем в тонких линиях.
Задача 2 Лист 2
ПЕРСПЕКТИВА ОБЪЕКТА
Даныортогональные проекции объекта (приложение Б)
Требуетсяпо ортогональным проекциям объекта (фасаду и плану) построить его перспективную проекцию.
Эпюр выполняется на листе чертежной бумаги формата А3.
(Пример выполнения приведён на рисунке 4)
Для выполнения задания рассмотреть пример в учебнике [6, с. 226, 227, рис. 567 – 569 и с. 255 –257, рис. 629 – 631; 7, с. 151 – 156, рис. 322 – 330].
Задание выполняют на листе чертёжной бумаге формата А1, А2 карандашом. В левом верхнем углу располагают ортогональные проекции сооружения, которые выбирают согласно своему варианту (Приложение Б) увеличив размеры проекций в 1,5 раза.
Алгоритм решения следующий:
Для того, чтобы обеспечить удачное перспективное изображение предмета, рекомендуется руководствоваться следующими правилами, выработанными практикой.
1.Картинную плоскость ориентируют так, чтобы её горизонтальный след О–О составлял с главным фасадом угол α от 25 до 300. Боковой фасад при этом получит сильное перспективное искажение, и изображение в целом получится более выразительным.
2.Точку стояния s следует выбирать так, чтобы угол β между проецирующими лучами, направленными в крайние точки плана предмета, составлял величину от 18 до 530. Оптимальное значение угла зрения равно 280
При этом главная точка Рдолжна располагаться в пределах средней трети участка картинной плоскости, охватываемой углом зрения.
3. Высоту горизонта обычно принимают на уровне глаза человека, стоящего на земле, т.е. h=1,5…1,7 м. В задании положение линии горизонта указано в исходных данных. Поскольку метод архитекторов предусматривает построение перспективы с использованием точек схода параллельных прямых двух основных направлений, то определяют точки схода горизонтальных и вертикальных линий плана.
 | Рисунок 4 Пример построения перспективы |
Для этого через точку стояния s проводят вертикальные и горизонтальные линии. Пересечение их с основанием картинной плоскости и даёт точку схода горизонтальных линий – точка F1 и вертикальных линий – точку F2. Определяется начало всех вертикальных линий плана – точки 1, 2, 3, 4, 5, 6, а также горизонтальных – точки 7и 8. На рисунке 5 изображен0 построение геометрического аппарата перспективы.
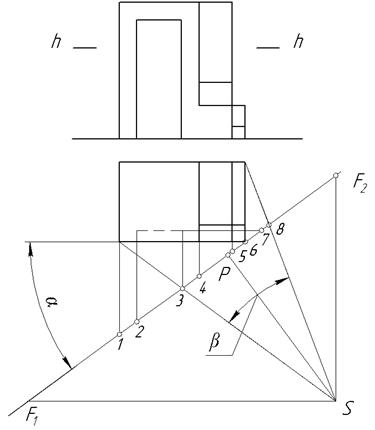
Рисунок 5 Геометрический аппарат для построения перспективы
Для большей наглядности перспективы её построение лучше выполнить в масштабе увеличения относительно размеров всех элементов ортогональных проекций. Размеры построения перспективы увеличить во столько раз, сколько раз расстояние между точками схода отложится на линии горизонта. При построении перспективы геометрического тела прежде строится перспектива его основания, т.е. перспектива плоской фигуры, лежащей в предметной плоскости, а именно перспектива плана заданного объекта. Строят картину (рисунок 6) и переносят на неё главную точку картины Р, для этого на основании картины О–О намечают основание точки Ри из неё восстанавливают перпендикуляр до пересечения с линией горизонта. На линии горизонта наносят точки F1иF2 на соответственных расстояниях от точки Р. На основании картины О–Онаносят точки начала прямых 1…8, которые наносят также на соответственных расстояниях вправо и влево от точки Р. Эти расстояния переносятся с ортогонального чертежа. Затем точки 1…6соединяют с точкой F2, а точки 6…8– с точкой F1. Пересечение этих линий даёт перспективу плана, также как и в ортогональных проекциях.
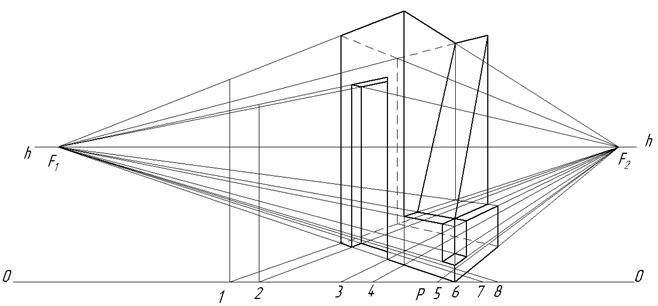 Рисунок 6. Построение перспективы
Рисунок 6. Построение перспективы
После того, как построена перспектива основания сооружения, приступают к построению его высоты. Через все вершины перспективы основания проводят вертикальные прямые. От точки 6на вертикальной линии откладывают истинную величину высоты ребра, которую берут с ортогонального чертежа в соответствующем масштабе, так как этот отрезок расположен в плоскости картины. Учитывая направление горизонтальных рёбер объекта, через вершину ребра 6проводят соответствующие линии в точки F1 и F2. Точки их пересечения с вертикальными прямыми определят высоту некоторых рёбер объекта.
Для того, чтобы построить перспективу ребра, основанием которого является точка пересечения линии 1 – F2и6 – F1, его по прямой 1 – F2 как бы выводят на картинную плоскость, т.е. высота этого ребра на картинной плоскости проецируется в натуральную величину, значение которой берут с ортогональных проекций и с учётом масштаба откладывают на вертикальной прямой, проведённой через точку 1. Из вершины построенного отрезка проводят линию в точку F2. Верхнее ребро бокового фасада объекта лежит на этой прямой. В пересечении с вертикальными прямыми, проведёнными из вершин перспективы плана, получают перспективу искомых рёбер. Аналогично определяют высоту перспективных проекций рёбер ниши.
Задача 3 лист 1
Проекции с числовыми отметками
Данплан земельного участка, рельеф которого задан горизонталями (рисунок 7)
Требуется: Построить линии пересечения откосов выемок и насыпей земляного сооружения (площадки и дороги) между собой и с топографической поверхностью. Принять уклон откосов выемок 1:1, насыпей 1:1,5 и уклон дороги 1:6;
Построить профиль (сечение) земляного сооружения плоскостью E-E.
Вариант задачи выбрать из таблицы по последней цифре шифра.
Таблица 1 Варианты задачи
| Номер варианта | ||||||||||
| Тип сооружения | А | Б | В | Г | А | Б | В | Г | А | Б |
| Отклонение оси сооружения от оси меридиана | С | СЗ | С | С | СВ | СЗ | ЮЗ | СЗ | СЗ | ЮВ 150 |
Для выполнения задания рассмотреть пример в учебнике [6, с. 170, 227, рис. 441 – 443 и с. 172 –175, рис. 445 – 453; 7, с. 151 – 156, рис. 322 – 330].
Эпюр выполняется в карандаше. Горизонтали топографической поверхности обводят тонкими линиями толщиной 0,1…0,2 мм. Контур земляного сооружения и линии пересечения откосов с топографической поверхностью и между собой обводят карандашом. Толщина линий 0,4…0,6 мм. Штриховку откосов выемок и насыпей выполняют линиями толщиной 0,1…0,2 мм перпендикулярно проектным горизонталям при расстоянии между бергштрихами 1,5…2,5 мм. Линии построения (в том числе проектные горизонтали) должны иметь толщину 0,1…0,2 мм. Для выполнения чертежа необходимо начертить в масштабе 1:200 план земельного участка, рельеф которого задан горизонталями (рисунок 7). Нанести на него в том же масштабе план земляного сооружения так, чтобы центр сооружения ÎÑ совпал с центром участка Î и ось сооружения была расположена к меридиану под заданным углом. Планы земляных сооружений приведены на рисунке 8 (размеры в метрах). Форму сооружения и угол наклона оси сооружения определяют по номеру варианта из таблицы 1.
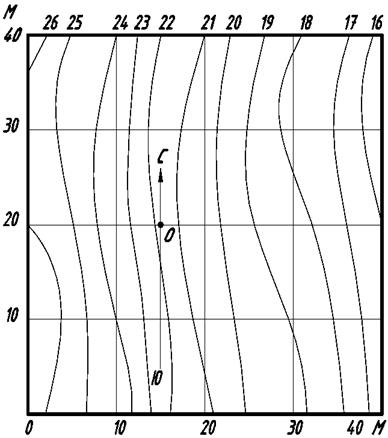 Рисунок 7 Рельеф земельного участка Рисунок 7 Рельеф земельного участка |
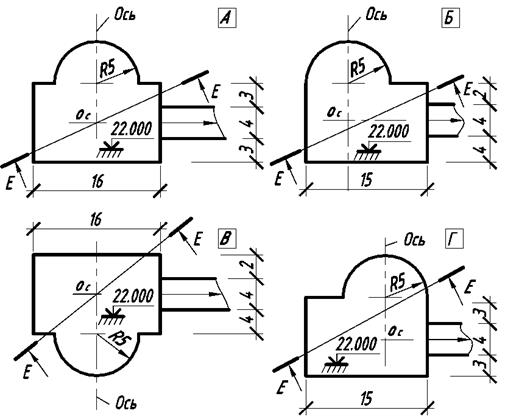 Рисунок 8 Планы земляных сооружений Рисунок 8 Планы земляных сооружений |
При выполнении эпюра исходят из следующих положений:
1. Точка в проекциях с числовыми отметками задается своей горизонтальной проекцией и числом при ней (отметкой), выражающей высоту этой точки в метрах над горизонтальной плоскостью, принятой за нулевую ;
2. Прямая линия задается проекциями двух точек и их отметками или отметкой одной точки и уклоном линии. Во втором случае должно быть указано направление, в котором прямая опускается (стрелкой);
3. Кривая линия задается необходимым числом проекций точек, принадлежащих кривой, и их отметками. Если кривая на всем протяжении имеет одинаковый уклон, ее можно задать проекцией линии, отметкой одной принадлежащей кривой точки и уклоном
4. Плоскость может быть задана проекциями трех точек, не лежащих на одной прямой, и их отметками; двумя параллельными или пересекающимися прямыми (прямые задаются в соответствии с п. 2); точкой и не проходящей через нее прямой (пп. 1 и 2). Кроме того, ее можно задать масштабом уклонов (градуированной линией ската) или одной горизонталью и уклоном. В последнем случае указывают направление уклона плоскости стрелкой [6, пп. 5.2, 5.3];
5. Если прямые параллельны, то параллельны их проекции, одинаковы уклон и его направление;
6. Линия пересечения плоскостей определяется точками пересечения двух однозначных горизонталей этих плоскостей;
7. Линия пересечения плоскости и поверхности или двух поверхностей определяется точками пересечения однозначных горизонталей обеих поверхностей (или плоскости и поверхности);
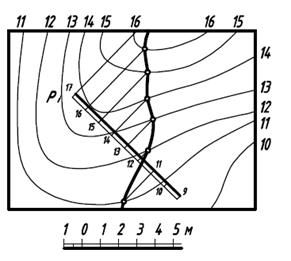 Рисунок 9 Пересечение плоскости и поверхности Рисунок 9 Пересечение плоскости и поверхности | На рисунке 9 показано пересечение плоскости и поверхности. Поверхность задана горизонталями, плоскость – масштабом уклона Рi 8. Для построения точки пересечения прямой с плоскостью или поверхностью нужно через прямую провести плоскость общего положения, задав ее произ- |
вольно выбранными горизонталями. Определив линию пересечения дополнительной плоскости с заданной плоскостью или поверхностью, отмечают на ней точку, в которой эта линия пересекается с заданной прямой (Рисунок 10);
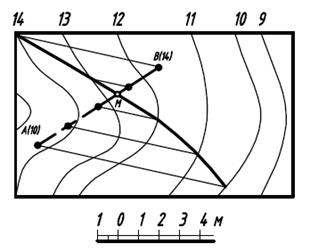 Рисунок 10 Пересечение прямой с поверхностью Рисунок 10 Пересечение прямой с поверхностью | 9. Чтобы построить точку пересечения кривой линии с плоскостью или поверхностью, следует градуировать ее и через полученные- точки провести горизонтали дополнительной цилиндрической поверхности (они взаимно параллельны). Построив линию пересечения дополнитель- |
ной поверхности с заданной плоскостью или поверхностью, отмечают на ней точку (точки), в которой эта линия пересекается с заданной кривой;
10. Так как топографическая поверхность в проекциях с числовыми отметками изображается большей частью с помощью горизонталей, то линию пересечения поверхности земляного сооружения (откосов) с топографической поверхностью можно построить, соединив точки пересечения однозначных горизонталей откосов и поверхности земли.
Приступая к работе над эпюром, следует определить из графика уклонов величину интервалов для откосов насыпей, откосов выемок и дороги в масштабе 1:200, затем нанести эти интервалы на масштабах уклонов откосов насыпей, выемок и дорог. Проведя проектные горизонтали откосов, определяют их пересечение между собой и соответствующими горизонталями топографической поверхности. Пример выполнения листа 3 приведен на рисунке 11.
З
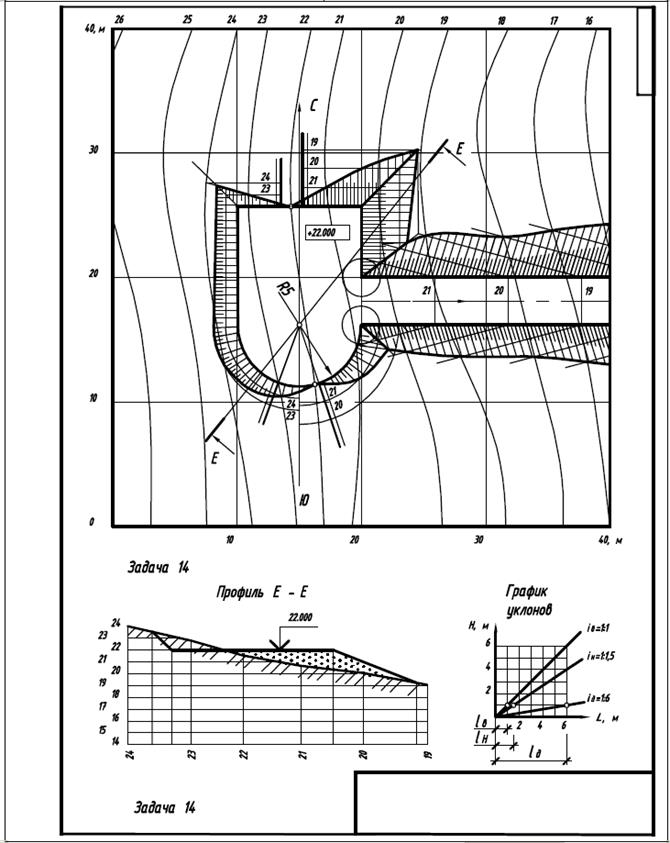
Рисунок 11 Пример выполнения листа 3
Задача 4 лист 1
