Лекция 2. Понятие об архитектуре компьютера
Содержание темы: Информационно-логические основы построения ЭВМ. Структурная и функциональная схема персонального компьютера. Классическая архитектура компьютера. Понятие об открытой архитектуре. Канальная и шинная системотехника. Состав, устройство и работа центральных и внешних устройств ЭВМ, их характеристики. Материнская плата. Устройства расширения. Микропроцессор. Регистры. Оперативная память (RAM) и её конструктивные элементы. Постоянная память (ROM). Модель доступа к памяти.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение:
НЕ Операция, выражаемая словом "не", называется отрицанием и обозначается чертой над высказыванием. Высказывание 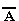 истинно, когда A ложно, и ложно, когда A истинно. Пример. "Луна — спутник Земли" (А); "Луна — не спутник Земли" (
истинно, когда A ложно, и ложно, когда A истинно. Пример. "Луна — спутник Земли" (А); "Луна — не спутник Земли" ( 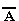 ).
).
И Операция, выражаемая связкой "и", называется конъюнкцией (лат. conjunctio — соединение) или логическим умножением и обозначается точкой " . " (может также обозначаться знаками 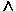 или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" — ложны.
или &). Высказывание А . В истинно тогда и только тогда, когда оба высказывания А и В истинны. Например, высказывание "10 делится на 2 и 5 больше 3" истинно, а высказывания "10 делится на 2 и 5 не больше 3", "10 не делится на 2 и 5 больше 3", "10 не делится на 2 и 5 не больше 3" — ложны.
ИЛИ Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение) или логическим сложением и обозначается знаком V (или +). Высказывание А v В ложно тогда и только тогда, когда оба высказывания А и В ложны. Например, высказывание "10 не делится на 2 или 5 не больше 3" ложно, а высказывания "10 делится на 2 или 5 больше 3", "10 делится на 2 или 5 не больше 3", "10 не делится на 2 или 5 больше 3" — истинны.
ЕСЛИ-ТО Операция, выражаемая связками "если ..., то", "из ... следует", "... влечет ...", называется импликацией (лат. implico — тесно связаны) и обозначается знаком 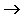 . Высказывание
. Высказывание 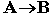 ложно тогда и только тогда, когда А истинно, а В ложно.
ложно тогда и только тогда, когда А истинно, а В ложно.
Каким же образом импликация связывает два элементарных высказывания? Покажем это на примере высказываний: "данный четырёхугольник — квадрат" (А) и "около данного четырёхугольника можно описать окружность" (В). Рассмотрим составное высказывание 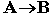 , понимаемое как "если данный четырёхугольник квадрат, то около него можно описать окружность". Есть три варианта, когда высказывание
, понимаемое как "если данный четырёхугольник квадрат, то около него можно описать окружность". Есть три варианта, когда высказывание 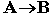 истинно:
истинно:
· А истинно и В истинно, то есть данный четырёхугольник квадрат, и около него можно описать окружность;
· А ложно и В истинно, то есть данный четырёхугольник не является квадратом, но около него можно описать окружность (разумеется, это справедливо не для всякого четырёхугольника);
- A ложно и B ложно, то есть данный четырёхугольник не является квадратом, и около него нельзя описать окружность.
Ложен только один вариант, когда А истинно, а В ложно, то есть данный четырёхугольник является квадратом, но около него нельзя описать окружность.
В обычной речи связка "если ..., то" описывает причинно-следственную связь между высказываниями. Но в логических операциях смысл высказываний не учитывается. Рассматривается только их истинность или ложность. Поэтому не надо смущаться "бессмысленностью" импликаций, образованных высказываниями, совершенно не связанными по содержанию. Например, такими: "если президент США — демократ, то в Африке водятся жирафы", "если арбуз — ягода, то в бензоколонке есть бензин".
РАВНОСИЛЬНО Операция, выражаемая связками "тогда и только тогда", "необходимо и достаточно", "... равносильно ...", называется эквиваленцией или двойной импликацией и обозначается знаком 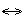 или ~. Высказывание
или ~. Высказывание 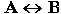 истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.
истинно тогда и только тогда, когда значения А и В совпадают. Например, высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 3", "23 делится на 6 тогда и только тогда, когда 23 делится на 3" истинны, а высказывания "24 делится на 6 тогда и только тогда, когда 24 делится на 5", "21 делится на 6 тогда и только тогда, когда 21 делится на 3" ложны.
Высказывания А и В, образующие составное высказывание 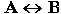 , могут быть совершенно не связаны по содержанию, например: "три больше двух" (А), "пингвины живут в Антарктиде" (В). Отрицаниями этих высказываний являются высказывания "три не больше двух" (
, могут быть совершенно не связаны по содержанию, например: "три больше двух" (А), "пингвины живут в Антарктиде" (В). Отрицаниями этих высказываний являются высказывания "три не больше двух" ( 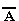 ), "пингвины не живут в Антарктиде" (
), "пингвины не живут в Антарктиде" ( 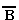 ). Образованные из высказываний А и В составные высказывания A
). Образованные из высказываний А и В составные высказывания A 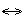 B и
B и 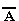
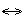
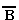 истинны, а высказывания A
истинны, а высказывания A 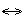
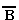 и
и 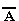
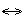 B — ложны.
B — ложны.
Итак, нами рассмотрены пять логических операций: отрицание, конъюнкция, дизъюнкция, импликация и эквиваленция.
Импликацию можно выразить через дизъюнкцию и отрицание: А 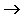 В = В = 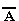 v В. Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию: А v В. Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию: А 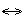 В = ( В = ( 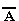 v В) . ( v В) . ( 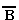 v А). v А). |
Таким образом, операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания ("не"), затем конъюнкция ("и"), после конъюнкции — дизъюнкция ("или") и в последнюю очередь — импликация.
| Логический элемент компьютера — это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию. |
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния — “1” и “0” в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению “истина” (“1”), а низкий — значению “ложь” (“0”).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
| Таблица истинности это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. |
С х е м а И
Схема И реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы И с двумя входами представлено на рис. 2.
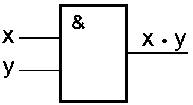 |  |
| Рис. 2 | Таблица истинности схемы И |
Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет ноль, на выходе также будет ноль.
Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x . y (читается как "x и y"). Операция конъюнкции на структурных схемах обозначается знаком "&" (читается как "амперсэнд"), являющимся сокращенной записью английского слова and.
С х е м а ИЛИ
Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на её выходе также будет единица.
Условное обозначение на структурных схемах схемы ИЛИ с двумя входами представлено на рис. 3. Знак "1" на схеме — от устаревшего обозначения дизъюнкции как ">=1" (т.е. значение дизъюнкции равно единице, если сумма значений операндов больше или равна 1). Связь между выходом z этой схемы и входами x и y описывается соотношением: z = x v y (читается как "x или y").
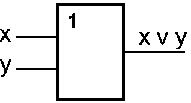 |  |
| Рис. 3 | Таблица истинности схемы ИЛИ |
С х е м а НЕ
Схема НЕ (инвертор) реализует операцию отрицания. Связь между входом x этой схемы и выходом z можно записать соотношением z = 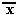 , где
, где 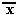 читается как "не x" или "инверсия х".
читается как "не x" или "инверсия х".
Если на входе схемы 0, то на выходе 1. Когда на входе 1, на выходе 0. Условное обозначение на структурных схемах инвертора — на рисунке 4.
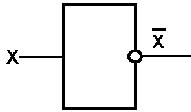 |  |
| Рис. 4 | Таблица истинности схемы НЕ |
С х е м а И—НЕ
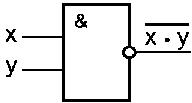
Схема И—НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И. Связь между выходом z и входами x и y схемы записывают следующим образом: 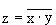 , где
, где 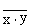 читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представлено на рисунке 5.
читается как "инверсия x и y". Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представлено на рисунке 5.
 |  |
| Рис. 5 | Таблица истинности схемы И-НЕ |
С х е м а ИЛИ—НЕ
Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ. Связь между выходом z и входами x и y схемы записывают следующим образом: 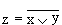 , где
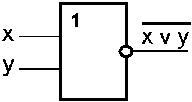
, где 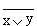 , читается как "инверсия x или y ". Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рис. 6.
, читается как "инверсия x или y ". Условное обозначение на структурных схемах схемы ИЛИ—НЕ с двумя входами представлено на рис. 6.
 |  |
| Рис. 5 | Таблица истинности схемы ИЛИ-НЕ |
| Триггер — это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое — двоичному нулю. |
Термин триггер происходит от английского слова trigger — защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает "хлопанье". Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить ("перебрасываться") из одного электрического состояния в другое и наоборот.
Самый распространённый тип триггера — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс). Условное обозначение триггера — на рис. 6.

Рис. 6
Он имеет два симметричных входа S и R и два симметричных выхода Q и 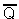 , причем выходной сигнал Q является логическим отрицанием сигнала
, причем выходной сигнал Q является логическим отрицанием сигнала 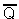 .
.
На каждый из двух входов S и R могут подаваться входные сигналы в виде кратковременных импульсов ( 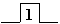 ).
).
Наличие импульса на входе будем считать единицей, а его отсутствие — нулем.
На рис. 7 показана реализация триггера с помощью вентилей ИЛИ—НЕ и соответствующая таблица истинности.
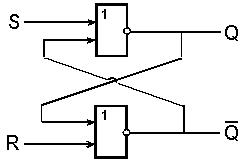 |  |
| Рис. 7 | Таблица истинности RS-триггера |
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы ИЛИ—НЕ (табл. 5.).
- Если на входы триггера подать S="1", R="0", то (независимо от состояния) на выходе Q верхнего вентиля появится "0". После этого на входах нижнего вентиля окажется R="0", Q="0" и выход
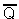 станет равным "1".
станет равным "1". - Точно так же при подаче "0" на вход S и "1" на вход R на выходе
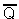 появится "0", а на Q — "1".
появится "0", а на Q — "1". - Если на входы R и S подана логическая "1", то состояние Q и
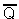 не меняется.
не меняется. - Подача на оба входа R и S логического "0" может привести к неоднозначному результату, поэтому эта комбинация входных сигналов запрещена.
Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 х 210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
