На постоянную нагрузку

Кинематический анализ

Система (рис. 1) состоит из фермы, представляющей собой геометрически неизменяемую конструкцию (Д = 1) и четырех балок (Д = 4), последовательно соединенных четырьмя простыми шарнирами (Ш = 4) и опирающихся на одну неподвижную (С_оп = 2) и пять подвижных (С_оп = 1) опор.

а) Количественная оценка неизменяемости системы

Определим число степеней свободы W:

W = 3Д – 2Ш – С_оп = 3∙5-2∙4 – 7 = 0

Необходимое условие статической определимости и геометрической неизменяемости выполняется.

б) Качественная оценка неизменяемости системы

Сборку и построение этажной схемы (рис. 2б) проводим методом триад, начиная с диска V, последовательно присоединяя к ней диски III, II и присоединяя диск IV.

Вывод: Система геометрически неизменяема, следовательно и статически определима.

Определение реакций в междисковых и опорных связях

Учитывая, что система статически определима и внешние нагрузки вертикальные, то все горизонтальные реакции в междисковых связях и неподвижной опоре узла 14 равны нулю.

Вертикальные реакции определяем в порядке разборки этажной схемы (рис. 2 б), составляя для каждого диска два уравнения равновесия типа

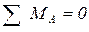, где A – номер одного из опорных узлов диска,

.

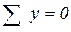Для диска I (рис. 2 в):

I. ;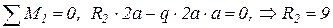

.

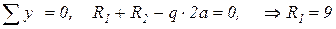Аналогично для дисков II, III, IV и V (рис. 2 г, д, е, ж):

II. ;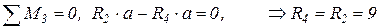

;

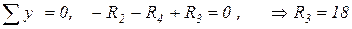III. ;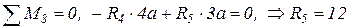

;

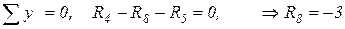IV. ;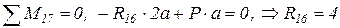

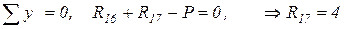
V. ;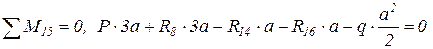

.

.

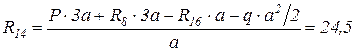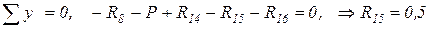Проверка(условия равновесия всей системы):

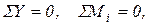где i - любая точка, выполняется.

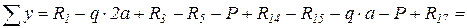0;

.

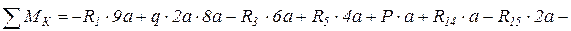
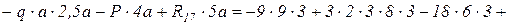
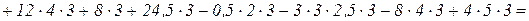
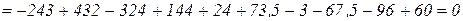На рис. 2 в-ж показаны результаты определения реакций (в кН).

Определение внутренних усилий и построение их эпюр

Определениевнутренних усилий (M, Q,) и построение эпюр проводим для каждого диска в отдельности методом простых сечений, а затем стыкуем построенные эпюры для конструкции в целом. Значения M откладываем со стороны растянутых волокон, знаки на этих эпюрах не ставим. На эпюре Q ставим знаки в соответствии с правилом знаков. Усилие Q считается положительным, если оно вращает выделенную часть по часовой стрелке. Усилие M считается положительным, если оно растягивает нижнее волокно выделенной части.

Эпюры M и Q. представлены на рис. 2 з,и.

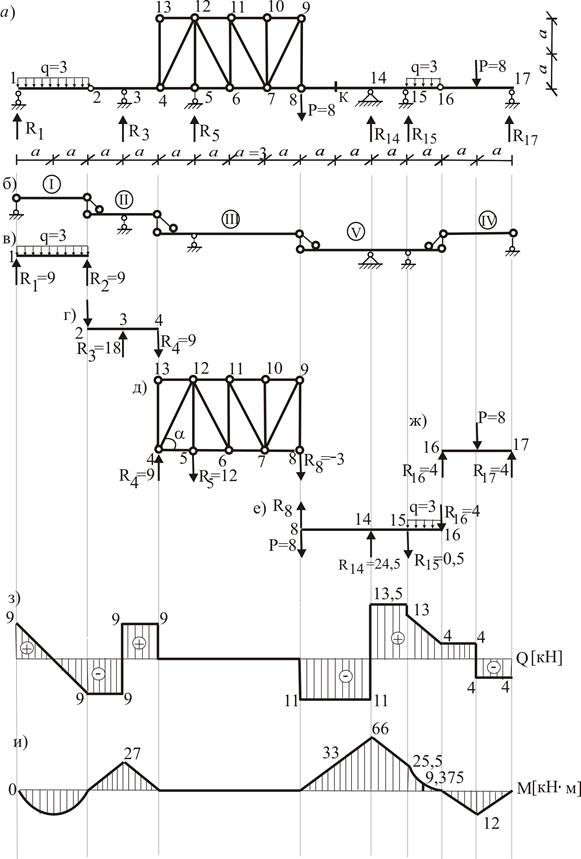
Рис. 2

Расчет фермы

Для выделенной из составной системы фермы (рис. 3) определяем продольные усилия N в стержнях методом вырезания узлов в порядке разборки, показанном на рис. 4.

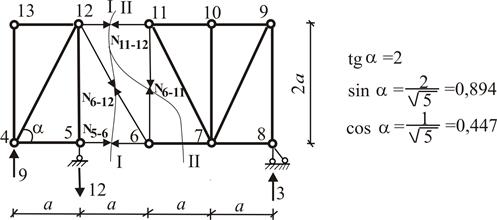
Рис. 3

1) ,

.

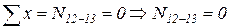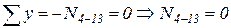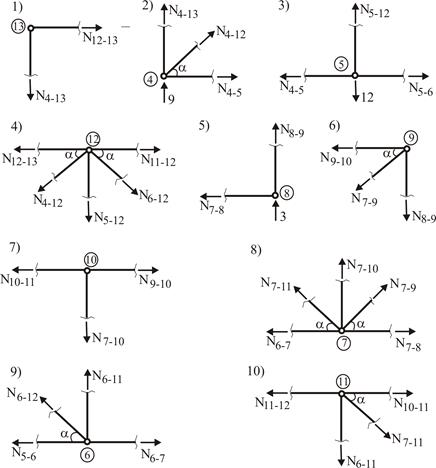
Рис. 4

2)

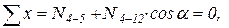
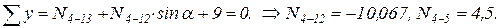
3) ,

.

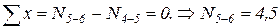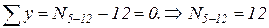4) ,

.

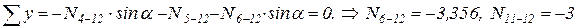5) ,

.

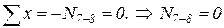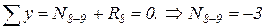6) ,

.

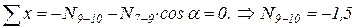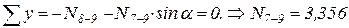7) ,

.

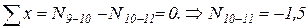8) .

.

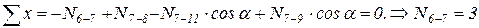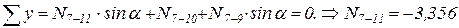9) ,

.

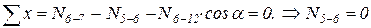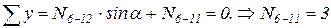10) ,

.

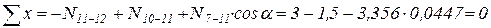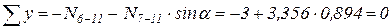Проверка

Проверим усилия в 4-х стержнях методом сквозных сечений (рис. 3).

Сечение I-I:

, .

, .

, .

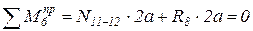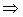
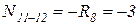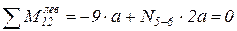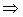
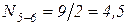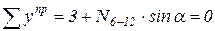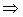
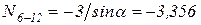Сечение II-II:

, .

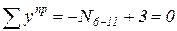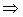
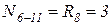Вывод. Усилия совпадают с вычисленными по методу вырезания узлов.

Результаты расчета сводим в таблицу:

№ ст.	4-5	5-6	6-7	7-8	9-10	10-11	11-12	12-13
Усилие	4,5	4,5			−1,5	−1,5	−3

№ ст.	4-13	5-12	6-11	7-10	8-9	4-12	6-12	7-11	7-9
Усилие					−3	−10,067	−3,356	−3,356	3,356

Задача 2. Расчет статически определимой составной системы

На подвижную нагрузку

1. Построение линий влияния опорных реакций и усилий M_k, Q_k

Статическим методом строим линии влияния всех опорных реакций и внутренних усилий M и Q в заданном сечении К рассмотренной в 1-ой задаче составной системы (рис. 1).

а) Линии влияния опорных реакций

Начнем с главной балки (балка V на рис. 2б).

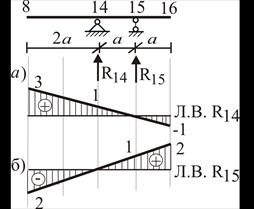Линии влияния этой балки показаны на рис. 5а, 5б (их можно построить по рис. 11 из приложения).

Затем эти результаты переносим на Л.В. R₁₄ и R₁₅ для всей балки в участке между точками 8-16 и, используя этажную схему (рис. 2б), распространяем линии влияния влево и вправо (рис. 7д, 7е). Аналогично строим линии влияния опорных реакций R₁, R₃, R₅, R₁₇ (рис. 7б, 7в, 7г, 7ж).

Рис. 5

б) Линии влияния M_k, Q_k

По рис. 6а (или рис. 12 из приложения) имеем:

1) Сила Р=1 слева от сечения К: 2) Сила Р=1 справа от сечения К:

, , .

; , .

, .

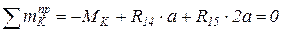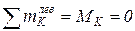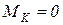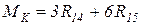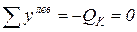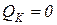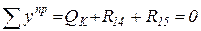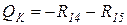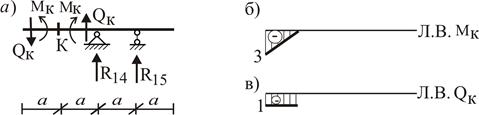
Рис. 6

Используя Л.В. R₁₄ и R₁₅ (рис. 5а,б) по полученным формулам строим Л.В. М_К и Q_К (рис. 6б,в). Затем их переносим на Л.В. составной системы на участок между точками 8-6 и распространяем влево и вправо (рис. 7з,и).

Все линии влияния проверяем кинематическим методом (рис. 13, 14).

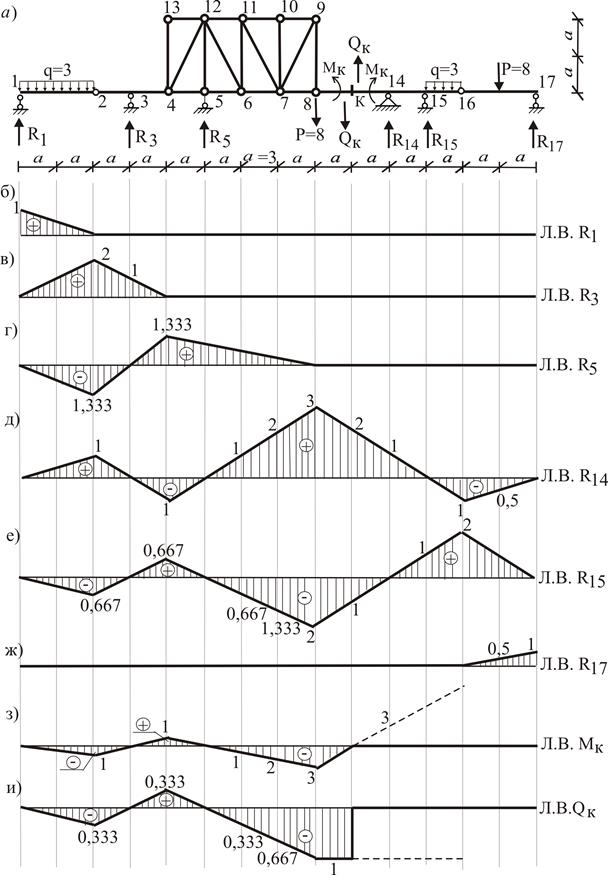
Рис. 7