Управляющий автомат мура
Автомат Мура отличается от Мили тем, что он описывается формулами Y=ƒ1(T), D=ƒ2(X,T). Т.е. его выходные сигналы зависят только от состояния триггеров. Поэтому его КС фактически распадается на 2 независимые КС – рис. 3.
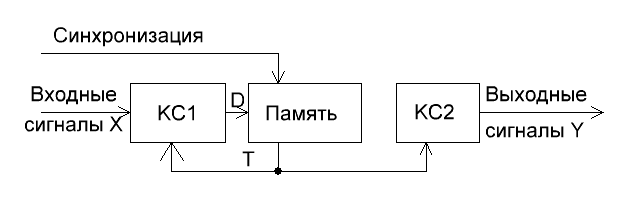
Рис. 3 Структура автомата Мура
КС1 реализует функцию D=ƒ2(X,T), а КС2 - Y=ƒ1(T).
Построим автомат Мура для того же примера:
| Сост. | x1 | x2 | y1 | y2 | y3 | y4 |
Сразу отметим, что состояния 2 и 5 для Мура полностью эквивалентны, т.к. они генерируют идентичные наборы выходных сигналов. Поэтому состояние 5 можно выбросить и добавить дополнительный переход из состояния 2 по сигналам x1x2=01 в состояние 0. Это действие заменит выброшенное 5-е состояние в плане переходов.
Исключение эквивалентных состояний в общем случае может сократить число триггеров автомата.
ТИ для КС1 (таблица переходов автомата):
| Сост. | T1 | T2 | T3 | X1 | x2 | D1 | D2 | D3 |
| 2a | ||||||||
| 2b (5) | ||||||||
Правила кодирования состояний те же, что и автомате Мили.
Коды состояний 001, 100, 101 и сочетание входных сигналов x1x2=10 не используются, это можно учитывать при минимизации.
Обратите внимание, что в таблице 2 строки, соответствующие состоянию 2. Строка 2b соответствует выброшенному состоянию 5. Видно, что из неё автомат переходит в состояние 0.
Получим минимальные формулы сигналов D1, D2 и D3 КС1:
Карта Карно для сигнала X1 – рис 4.
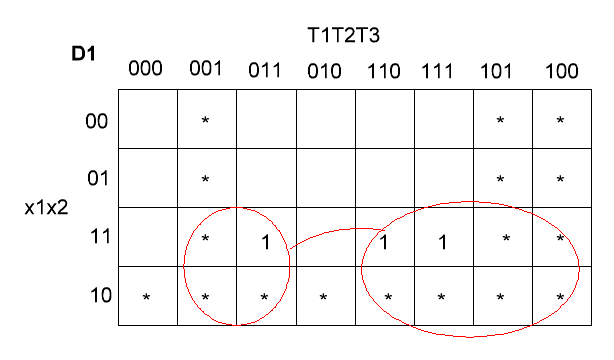
Рис 4. Карта Карно для сигнала X1.
Из карты следует, что D1 = x1. Это же видно из ТИ.
Аналогично:
D2 = x1 + T2 + T1 T2 T3 x2
D3 = T1 T2 T3 x2 + T2 + T1 T2 T3 x1
ТИ для КС2 автомата:
| Сост. | T1 | T2 | T3 | y1 | y2 | y3 | y4 |
Сигналы:
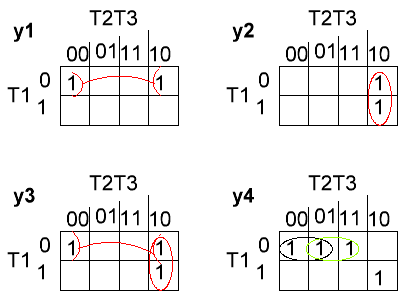
Рис.5 Карты Карно для сигналов y1-y4
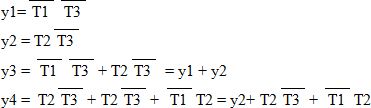
Из анализа формул видно, что y3 и y4 можно формировать, используя уже готовые y1 и y2. Это может дополнительно упростить КС2, но на практике такое решение снижает нагрузочную способность схемы на выходах y1 и y2.
Также, можно упростить реальную схему, если в каком-то смысле объединять схемы КС1 и КС2, формируя общие для них внутренние сигналы (например, T1 T3) и использовать их одновременно в обоих схемах. Конечно, обращая внимание на длину получаемых цепочек элементов и на их быстродействие (при увеличении длины цепочки падает её быстродействие).
Даже несмотря на то, что при рассмотрении автомата Мили мы не минимизировали его формулы, можно заметить, что автомат Мура проще уже потому, что для формирования Y не нужны сигналы X.
