Итерационная процедура формирования сети
Функция net = newrb(Р,Т,GOAL,SPREAD), где Р — массив входных векторов, Т — массив целей,GOAL — допустимая среднеквадратичная ошибка сети, SPREAD — "параметр влияния" создает сеть, добавляя по одному нейрону на каждом шаге обучения. Сначала первый слой не содержит нейронов. Сеть моделируется и определяется вектор входа, дающий наибольшую погрешность сети. В первый слой добавляется нейрон с весами, равными этому вектору входа. Веса линейного слоя находятся из решения системы линейных алгебраических уравнений, как в функции newrbe, но система будет с прямоугольной матрицей. На втором шаге аналогично находится вектор, дающий наибольшую погрешность и добавляется нейрон первого слоя с весами, равными этому вектору. Так продолжается, пока среднеквадратичная ошибка сети не станет меньше заданной величины GOAL.
С помощью функции newrb создадим такую же сеть, которую создали с помощью функции newrbe.
>> P = -1:.1:1;
и соответствующими значениями функции (выходами)
>> T = [-.9602 -.5770 -.0729 .3771 .6405 .6600 .4609 ...
.1336 -.2013 -.4344 -.5000 -.3930 -.1647 .0988 ...
.3072 .3960 .3449 .1816 -.0312 -.2189 -.3201];
Построим график обучающего множества (рис. 4.8):
>> plot(P,T,'*r','LineWidth', 2)
>> grid on
>> xlabel('Входной вектор P');
>> ylabel('Целевой вектор T');
>> hold on
Рис. 4.8. Обучающее множество для функции newrb
Естественно, графики рис. 4.4 и 4.8 совпадают.
Зададим допустимую погрешность:
>>goal=0.01;
Создадим сеть (параметр SPREAD по умолчанию равен 1):
>> net=newrb(P,T,goal);
NEWRB, neurons = 0, MSE = 0.176192
NEWRB, neurons = 2, MSE = 0.160368
NEWRB, neurons = 3, MSE = 0.128338
NEWRB, neurons = 4, MSE = 0.0275185
NEWRB, neurons = 5, MSE = 0.0264878
NEWRB, neurons = 6, MSE = 0.00046188
График обучения сети показан на рис. 4.9
Рис. 4.9. График обучения сети
Число эпох на графике рис. 4.9 равно числу нейронов первого слоя, в нашем случае – 6. Число нейронов первого слоя можно найти и такой командой:
>> net.layers{1}.size
ans =
Найдем координаты центров радиальных базисных функций (в терминах NNT MATLAB – это веса первого слоя):
>> net.IW{1}
ans =
-1.0000
-0.9000
-0.8000
-0.7000
1.0000
-0.6000
Легко проверить, что для обучающего множества сеть очень точно аппроксимирует функцию.
Повторим пример аппроксимации функции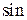 
. Для выполнения примера надо повторить все команды, использовавшиеся в эксперименте, заменив функцию newrbe на newrb. Результаты (рис. 4.10) близки к результатам использования функции со всеми её недостатками. Но число нейронов первого слоя сократилось.
Рис. 4.10. Результаты моделирования работы сети, созданной функцией newrb
Задания
1. Используя градиентный метод обучения, постройте радиальную базисную нейронную сеть, аппроксимирующую заданную функцию:
а)  | б)  |
в)  | д)  |
е)  | ж)  |
СЕТИ ХОПФИЛДА
Архитектура сети
Особенностью архитектуры рекуррентных сетей является наличие блоков динамической задержки и обратных связей. Всякий целевой вектор можно рассматривать как набор характерных признаков некоторого объекта. Если создать рекуррентную сеть, положение равновесия которой совпадало бы с этим целевым вектором, то такую сеть можно было бы рассматривать как ассоциативную память. Поступление на вход такой сети некоторого набора признаков в виде начальных условий приводило бы ее в то или иное положение равновесия, что позволяло бы ассоциировать вход с некоторым объектом. Именно такими ассоциативными возможностями и обладают сети Хопфилда. Они относятся к классу рекуррентных нейронных сетей, обладающих тем свойством, что за конечное число тактов времени они из произвольного начального состояния приходят в состояние устойчивого равновесия, называемое аттрактором. Количество таких аттракторов определяет объем ассоциативной памяти сети Хопфилда.
Спроектировать сеть Хопфилда — значит создать рекуррентную сеть с множеством точек равновесия, таких, что при задании начальных условий сеть в конечном счете приходит в состояние покоя в одной из этих точек. Свойство рекурсии проявляется в том, что выход сети подается обратно на вход. Можно надеяться, что выход сети установится в одной из точек равновесия. Известные методы синтеза сети Хопфилда не являются абсолютно совершенным в том смысле, что синтезируемая сеть в дополнение к желаемым может иметь паразитные точки равновесия. Однако число таких паразитных точек должно быть сведено к минимуму за счет конструирования метода синтеза. Более того, область притяжения точек равновесия должна быть максимально большой.
В Neural Networks Toolbox системы MATLAB используем метод синтеза модифицированной сети Хопфилда, основанный на построении системы линейных дифференциальных уравнений первого порядка, которая задана в некотором замкнутом гиперкубе пространства состояний и имеет решения в вершинах этого гиперкуба [12]. Такая сеть несколько отличается от классической модели Хопфилда, но она проще для понимания и проектирования, и мы будем ссылаться на нее как на модифицированную сеть Хопфилда.
Архитектура модифицированной сети Хопфилда представлена на рис. 5.1. Вход p устанавливает значения начальных условий. Сеть представляет собой симметричный насыщенный линейный слой (Symmetric saturated linear layer). Сеть работает по тактам (шагам). Выход сети a1(k) — выход сети на k‑ом такте работы. Начальные условия имеют вид a1(k)= p. Задержка на один такт обозначена на рис. 5.1 как D.
Рис. 5.1. Архитектура сети Хопфилда
Сеть Хопфилда использует линейную функцию активации с насыщением satlins (рис. 5.2).
Рис. 5.2. Линейная функция активации с насыщением
Для входов меньше, чем -1 функция satlins дает -1. Для входа в диапазоне от -1 до +1 функция просто возвращает исходное значение. Для входов больше, чем 1 возвращает 1.
Сеть Хопфилда может быть промоделирована с одним или большим количеством векторов входа, которые задаются как начальные условия. После того как начальные условия заданы, сеть генерирует выход, который по обратной связи подается на вход. Этот процесс повторяется много раз, пока выход не установится в положение равновесия. Можно надеяться, что каждый выходной вектор, в конечном счете, сойдется к одной из точек равновесия, наиболее близкой к входному сигналу.
Сеть Хопфилда описывается следующим образом
,
где 
— матрица весов, 
— вектор смещения.
Создание сети