Е.1.5.2 Первый метод для расчета амплитуды поперечных колебаний
Е.1.5.2.1 Расчет перемещения
(1) Максимальное перемещение yF,max рассчитывают по формуле (Е.7)
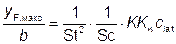 , (Е.7)
, (Е.7)
где St — число Струхаля по таблице Е.1;
Sc — число Скрутона по Е.1.3.3;
Kw — коэффициент приведенной длины по Е.1.5.2.4;
К — коэффициент формы колебаний по Е.1.5.2.5;
сlat — аэродинамический коэффициент вихревого возбуждения по таблице Е.3.
Примечание — Аэродинамические силы учитываются через коэффициент корреляции длины Kw.
Е.1.5.2.2 Аэродинамический коэффициент вихревого возбуждения сlat
(1) Базовые значения аэродинамических коэффициентов вихревого возбуждения сlat,0 указаны
в таблице Е.2.
Таблица Е.2 — Базовые значения аэродинамических коэффициентов вихревого возбуждения сlat
для разных поперечных сечений
| Поперечное сечение | сlat,0 |
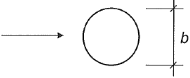 Для всех чисел Рейнольдса Для всех чисел Рейнольдса | См. рисунок Е.2 |
Окончание таблицы Е.2
| Поперечное сечение | сlat,0 | |
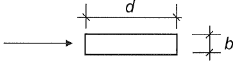 0,5 £ d/b £ 10 0,5 £ d/b £ 10 | 1,1 | |
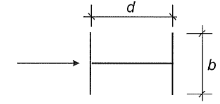 Допустима линейная интерполяция Допустима линейная интерполяция | d/b = 1 | 0,8 |
| d/b = 1,5 | 1,2 | |
| d/b = 2 | 0,3 | |
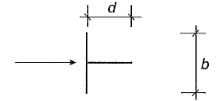 Допустима линейная интерполяция Допустима линейная интерполяция | d/b = 1 | 1,6 |
| d/b = 2 | 2,3 | |
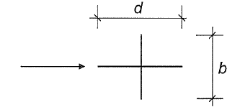 Допустима линейная интерполяция Допустима линейная интерполяция | d/b = 1 | 1,4 |
| d/b = 2 | 1,1 | |
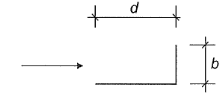 Допустима линейная интерполяция Допустима линейная интерполяция | d/b = 1,3 | 0,8 |
| d/b = 2,0 | 1,0 | |
| Примечание — Экстраполяция коэффициентов вихревого возбуждениякак функции d/b не допускается. |
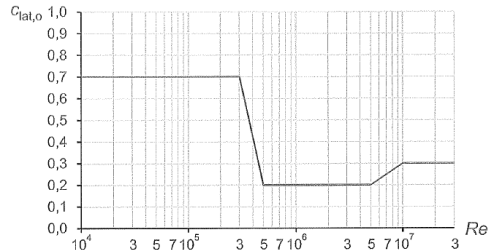
Рисунок Е.2 — Базовые значения аэродинамических коэффициентов
вихревого возбуждения clat,0 в зависимости
от числа Рейнольдса Re(vcrit,i) для круговых цилиндров, см. Е.1.3.4
(2) Аэродинамический коэффициент вихревого возбуждения clat указан в таблице Е.3.
Таблица Е.3 — Аэродинамический коэффициент вихревого возбуждения clat в зависимости от отношения критической скорости ветра к средней скорости ветра vcrit,i/vm,Lj
| Критическое отношение скоростей ветра | clat |
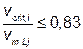 |  clat = clat,0 clat = clat,0 |
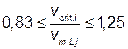 | 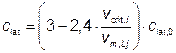 |
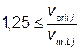 | clat = 0 |
| Где clat,0 — основное значение clat по таблице Е.2 и для круговых цилиндров по рисунку Е.2; vcrit,i — критическая скорость ветра (см. формулу (Е.1)); vm,Lj — средняя скорость ветра (см. 4.3) в середине эффективной приведенной длины по рисунку Е.3. |
Е.1.5.2.3 Корреляционная длина Lj
(1) Корреляционная длина Lj должна размещаться в области пучности колебаний. Примеры приведены на рисунке Е.3. Для мачтовых вышек с оттяжками и многопролетных мостов требуются специальные исследования.
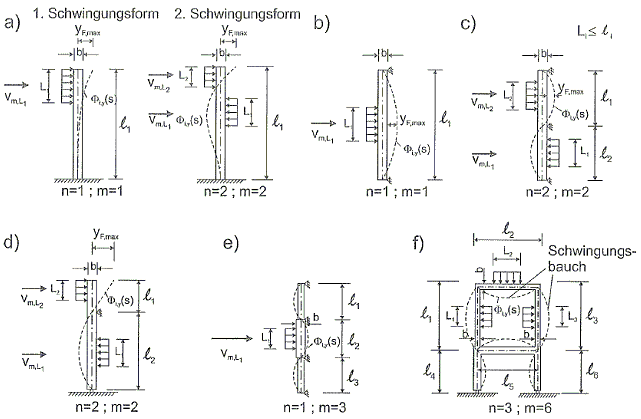
| Schwingungsform | Форма колебаний |
| Schwingungsbauch | Пучность колебаний |
Примечание — При указании более одной корреляционной длины, их применяют одновременно с использованием наибольшего значения clat.
Рисунок Е.3 — Примеры использования корреляционной длины Lj (j = 1, 2, 3)
Таблица Е.4 — Корреляционная длина Lj как функция амплитуды колебаний yF(sj)
| yF(sj)/b | Lj/b |
| <0,1 | |
| 0,1 – 0,6 | 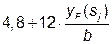 |
| >0,6 |
Е.1.5.2.4 Коэффициент эффективной корреляционной длины Кw
(1) Коэффициент эффективной корреляционной длины Кw следует определять по формуле (Е.8).
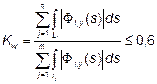 , (Е.8)
, (Е.8)
где FI,y — i-ая форма колебаний (см. F.3);
Lj — корреляционная длина;
lj — длина конструкции между двумя узловыми точками (см. рисунок Е.3); для консольных систем длина идентична высоте конструкции;
n — количество зон, в которых одновременно возникает вихревое возбуждение (см. рисунок Е.3);
m — количество пучностей колебаний учитываемой формы колебаний Fi,y колеблющейся системы;
s — координата по рисунку Е.5.
(2) Для некоторых простых конструкций, которые колеблются в основной форме и на которые воздействует вихревое возбуждение, как в таблице Е.5, коэффициент приведенной длины Kw допускается определять приближенно по формулам, приведенным в таблице Е.5.
Таблица Е.5 — Коэффициент эффективной корреляционной длины Kw и коэффициент К формы
колебаний простых конструкций
