АРХИТЕКТУРЫ МИКРОПРОЦЕССОРА — RISC И CISC
Основные черты CISC-концепции:
Ранее других появились процессоры CISC. Термин CISC означает сложную систему команд и является аббревиатурой английского определения Complex Instruction Set Computer. Благодаря этому процессоры выполняют самые разнообразные задачи обработки данных.
При разработке набора команд CISC заботились об удобстве программиста/компилятора, а не об эффективности исполнения команд процессором. В систему команд вводили много сложных команд (производящих по несколько простых действий). Часто эти команды представляли собой программы, написанные на микрокоде и записанные в ПЗУ процессора. Команды CISC имеют разную длину и время выполнения. Зато машинный код CISC-процессоров — язык довольно высокого уровня. В наборе команд CISC часто присутствуют, например, команды организации циклов, команды вызова подпрограммы и возврата из подпрограммы, сложная адресация, позволяющая реализовать одной командой доступ к сложным структурам данных. Основной недостаток CISC — большая сложность реализации процессора при малой производительности.
Примеры CISC-процессоров — семейство Motorola 680x0 и процессоры фирмы Intel от 8086 до Pentium II. Наиболее известные микроконтроллеры с CISC-архитектурой фирм Zilog, Intel, Motololla, Siemens.
Основные черты RISC-концепции:
Со временем стало необходимо повысить скорость работы процессоров. Одним из путей к этому стал процессор RISC, который характеризуется сокращенным набором быстро выполняемых команд и происходит от английского Reduced Instruction Set Computer.
-одинаковая длина команд;
-одиаковый формат команд — код команды регистр-приемник два регистра-источника;
-операндами команд могут быть только регистры;
-команды выполняют только простые действия;
-большое количество регистров общего назначения (могут быть использованы любой командой);
-конвейер(ы);
-выполнение команды не дольше, чем за один такт;
-простая адресация.
К RISC процессорам причисляют MIPS, SPARC, PowerPC, DEC Alpha, HP PA-RISC, Intel 960, AMD 29000. RISC-концепция предоставляет компилятору большие возможности по оптимизации кода. Существуют стандарты на RISC-процессоры, например SPARC — Scalable Processor ARChitecture, MIPS, PowerPC часто их называют открытыми архитектурами. Наиболее известные микроконтроллеры с RISC-архитектурой это семейства AT90S, ATMega, ARM фирмы Atmel, микроконтроллеры фирм PIC, Scenix, Holtek.
СРАВНЕНИЕ АРХИТЕКТУР RISC И CISC.
Основная идея RISC-архитектуры — это тщательный подбор таких комбинаций кодов операций, которые можно было бы выполнить за один такт тактового генератора. Основной выигрыш от такого подхода — резкое упрощение аппаратной реализации ЦП и возможность значительно повысить его производительность.
Однако обычно выигрыш от повышения быстродействия в рамках ^ RISC-архитектуры перекрывает потери от менее эффективной системы команд, что приводит к более высокой эффективности RISC-систем в целом по сравнению с CISC. Так, в процессоре CISC для выполнения одной команды необходимо, в большинстве случаев, 10 и более тактов. Что же касается процессоров RISC, то они близки к тому, чтобы выполнять по одной команде в каждом такте. Также с упрощением ЦП уменьшается число транзисторов, необходимых для его реализации, следовательно, уменьшается площадь кристалла. А с этим связано снижение стоимости и потребляемой мощности.
Следует также иметь в виду, что благодаря своей простоте процессоры RISC не патентуются. Это также способствует их быстрой разработке и широкому производству. Между тем, в сокращенный набор RISC вошли только наиболее часто используемые команды. Ряд редко встречающихся команд процессора CISC выполняется последовательностями команд процессора RISC. Позже появилась концепция процессоров MISC, использующая минимальный набор длинных команд. Вслед за ними возникли процессоры VLIW, работающие со сверхдлинными командами. Быстродействие процессоров определяется в миллионах операций в секунду MIPS.
ЭЛЕМЕНТАРНАЯ КОНЪЮНКЦИЯ, И ЕЕ РАНГ. ДИЗЪЮНКТИВНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ (ДНФ И СДНФ).ЗАПИСЬ СДНФ ПО ТАБЛИЦАМ ИСТИННОСТИ И ПРЕДСТАВЛЕНИЕ ПО НЕЙ ФУНКЦИОНАЛЬНОЙ СХЕМЫ. ПРОСТАЯ ИМПЛИКАНТА И СОКРАЩЕННАЯ ДНФ.
Конъюнкцией (или логическое умножение) двух булевых переменных называется следующая функция f(x1,x2)=x1x2=min(x1,x2)
Дизъюнкцией (логическое сложение) двух булевых переменных называется следующая функция g(x1,x2)=x1Vx2=max(x1,x2)
Переменная x или x называется литералом (или буквой).
Конъюкция литералов, встречающихся не более чем по одному разу, называется элементарной конъюнкцией. Число букв входящих в неё называется её рангом. Элементарная конъюнкция называется полной относительно рассматриваемой булевой функции, если её ранг равен числу переменных данной функции.
Дизъюнкция конечного множества элементарных конъюнкций называется дизъюнктивной нормальной формой(ДНФ). Число элементарных конъюнкций, образующих дизъюнктивную нормальную форму(ДНФ) называется длиной ДНФ. ДНФ содержащая только полные элементарные конъюнкции называется совершенной ДНФ(или СДНФ). Любую логическую формулу А можно представить в виде ДНФ, а затем ДНФ в виде СДНФ.
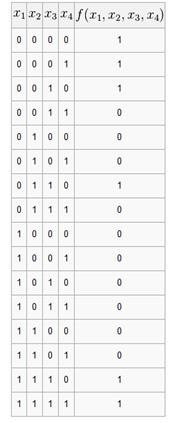Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности статьи минимизация логических функций методом Квайна, в которой нахождение СДНФ встречается несколько раз:
В ячейках результата f(x1,x2,x3,x4)отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.
Первая строка содержит 1 в указанном поле. Отмечаются значения всех четырёх переменных, это:
· x1=0
· x2=0
· x3=0
· x4=0
Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: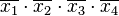 
Переменные второго члена:
· x1=0
· x2=0
· x3=0
· x4=1
x4 в этом случае будет представлен без инверсии: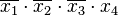 
Таким образом анализируются все ячейки f(x1,x2,x3,x4). Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).
Совершенная ДНФ этой функции:
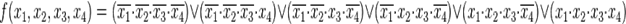
37. ДВОИЧНЫЕ ПЕРЕМЕННЫЕ И ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ. ЭЛЕМЕНТАРНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ.
В булевой алгебре различают двоичные переменные и переключательные функции.
Двоичные переменные могут принимать два значения: 0 и 1. Они называются также логическими или булевыми переменными и обозначаются символами х1,x2,х3,...
Переключательные функции (ПФ) зависят от двоичных переменных. Они, как и аргументы, могут принимать лишь два значения: 0 или 1. ПФ называют также логическими или булевыми функциями. Будем обозначать ПФ в виде f(х1,x2,х3,...). указывая в скобках аргументы, либо в виде y1,y2,y3,... . ПФ в свою очередь могут служить аргументами еще более сложных логических функций. Следовательно, можно построить ПФ любой заранее заданной сложности, пользуясь ограниченным числом логических связей.
ПФ принято задавать таблицами истинности, в которых для всех наборов переменных указываются соответствующие им значения ПФ. Формирование значений ПФ в таблице истинности выполняется в соответствии с логикой работы устройства (сумматора, сдвигателя, преобразователя кодов и т. д.).
Элементарные логические функции:
1) Элемент «И» (AND)
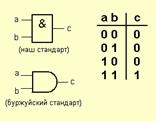единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.
2) Элемент «ИЛИ» (OR)
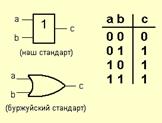На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.
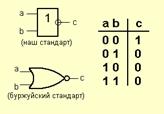
3) Элемент «НЕ» (NOT)
4) Элемент «И-НЕ» (NAND) 5) Элемент «ИЛИ-НЕ» (NOR)
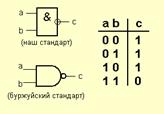
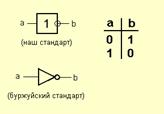
6)
Элемент «Исключающее ИЛИ» (XOR)
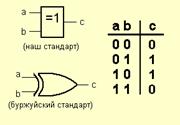
Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0.
ЭЛЕМЕНТАРНАЯ ДИЗЪЮНКЦИЯ, И ЕЕ РАНГ. КОНЪЮКТИВНЫЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ (КНФ И СКНФ). ЗАПИСЬ СКНФ ПО ТАБЛИЦАМ ИСТИННОСТИ.
Элементарная дизъюнкция — дизъюнкция конечного множества логических переменных и их инверсий.
Число аргументов, образующих элементарную дизъюнкцию или конъюнкцию, называется ее рангом.
Пример 1. Х & Y & Z, Х &. Y & Z — элементарные конъюнкции третьего ранга. Х v Y, Х v Y — элементарные дизъюнкции второго ранга.
Конъюнктивной нормальной формой (КНФ) ПФ называется конъюнкция (логическое произведение) элементарных дизъюнкций.Например, функции
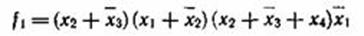
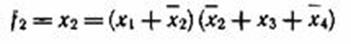
заданы в КНФ. Ранг элементарной дизъюнкции определяется числом переменных, входящих в эту дизъюнкцию.
Совершенной КНФ (СКНФ) ПФ, имеющей n аргументов, называется такая форма, в которой все дизъюнкции имеют ранг n. СКНФ переключательной функции составляется по таблице истинности по наборам, при которых ПФ принимает нулевые значения. Каждому такому набору ставится в соответствие элементарная дизъюнкция ранга n, и все эти дизъюнкции соединяются символами конъюнкции. При этом в дизъюнкциях с отрицанием берутся те переменные, которые на соответствующем наборе имеют единичное значение.
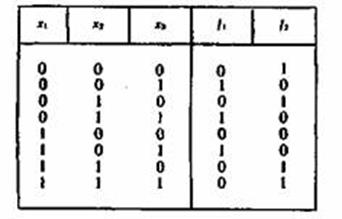
Для функций f1 и f2, заданных в табл. 3.1, можно записать следующие СКНФ:
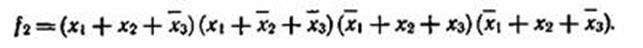
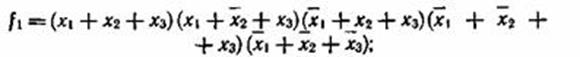Элементарные дизъюнкции СКНФ называют конституентами нуля, так как они соответствуют наборам, на которых ПФ принимает значение 0.