Строчные буквы греческого алфавита. A — угол между направлением оси х и усилием для перфорированного листа из металла;

a — угол между направлением оси х и усилием для перфорированного листа из металла; угол между направлением усилия и волокнами древесины; угол между направлением усилия и загруженным торцом;

b — угол между направлением волокна и усилием для перфорированного листа из металла;

b_с — коэффициент прямолинейности;

g — угол между направлением оси х и линией соединения деревянного элемента посредством перфорированного листа из металла;

g_M — частичный коэффициент свойств материала, также учитываемый для модели неопределенности и изменений размеров;

l_y — коэффициент гибкости при изгибе относительно оси у;

l_z — коэффициент гибкости при изгибе относительно оси z;

l_rel,y — относительный коэффициент гибкости при изгибе относительно оси у;

l_rel,z — относительный коэффициент гибкости при изгибе относительно оси z;

r_a — плотность;

r_k — нормативная плотность;

r_m — средняя плотность;

s_с,0,d — расчетное напряжение при сжатии вдоль волокон;

s_с,a,d — расчетное напряжение при сжатии под углом a к волокнам;

s_f,c,d — среднее расчетное напряжение сжатия полки;

s_f,c,max,d — расчетное напряжение сжатия крайних волокон полки;

s_f,t,d — среднее расчетное напряжение растяжения полки;

s_f,t,max,d — расчетное напряжение растяжения крайних волокон полки;

s_m,сrit — критическое напряжение при изгибе;

s_m,y,d — расчетное изгибающее напряжение относительно оси у;

s_m,z,d — расчетное изгибающее напряжение относительно оси z;

s_m,a,d — расчетное напряжение при изгибе под углом a к волокнам;

s_N — осевое напряжение;

s_t,0,d — расчетное растягивающее напряжение вдоль волокон;

s_t,90,d — расчетное растягивающее напряжение перпендикулярно волокнам;

s_w,c,d — расчетное напряжение сжатия стенки;

s_w,t,d — расчетное напряжение растяжения стенки;

t_d — расчетное напряжение сдвига;

t_F,d — расчетное напряжение анкерного крепления от осевого усилия;

t_M,d — расчетное напряжение анкерного крепления от момента;

t_tor,d — расчетное напряжение сдвига от кручения;

y₀ — коэффициент комбинации переменного воздействия;

y₂ — коэффициент квазипостоянной величины переменного воздействия;

x — модальный коэффициент затухания.

Основы проектирования

Требования

Базовые требования

(1)Р Расчет деревянных конструкций производится в соответствии с общими правилами, приведенными в EN 1990.

(2) Дополнительные положения, касающиеся деревянных конструкций, также приводятся в настоящем разделе.

(3) Базовые требования EN 1990 (раздел 2) считаются удовлетворительными для деревянных конструкций, когда применяется расчет по предельным состояниям в сочетании с методом частных коэффициентов с использованием EN 1990:2002 и EN 1991 — для воздействий и их сочетаний, а также EN 1995 — для устойчивости, положений по пригодности к эксплуатации и долговечности.

Управление надежностью

(1) Когда требуются различные уровни надежности, то предпочтительным является соответ­ствующим образом назначенное качество исполнения в соответствии с EN 1990:2002 (приложение С).

Расчетный период эксплуатации и долговечность

(1) Применяется по 2.3 EN 1990.

Принципы расчета по предельным состояниям

Общая часть

(1)Р Расчетные модели для различных типов предельных состояний должны учитывать следующее:

— различные свойства материала (например, модуль упругости, прочность и вид разрушения);

— поведение материалов с учетом фактора времени (ползучесть);

— различные климатические условия (температура, влажность, вибрации);

— различные расчетные ситуации (этапы строительства, изменение условий опирания).

Предельные состояния

(1)Р При проведении структурного анализа следует использовать следующие свойства жесткости:

— для линейно-упругого анализа первого порядка, при котором внутренние силы не зависят
от распределения жесткости внутри элемента (т. е. если элементы имеют те же самые зависящие
от времени свойства), принимаются средние значения;

— для линейно-упругого анализа первого порядка, при котором внутренние силы зависят от распределения жесткости внутри элемента (для композитов, состоящих из материалов, с различными зависящими от времени свойствами), окончательно принимаются значения, соответствующие нагрузке, вызывающей наибольшее напряжение по отношению к прочности;

— для линейно-упругого анализа второго порядка принимаются расчетные значения, не учитывающие длительность действия нагрузки.

Примечание 1 — Окончательно средние значения в соответствии с длительностью действия нагрузки принимаются согласно 2.3.2.2(2).

Примечание 2 — Расчетные значения жесткостных характеристик — см. 2.4.1(2)Р.

(2) Модуль скольжения для предельного состояния K_u следует принимать:

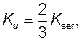(2.1)

где K_ser — мгновенный модуль скольжения, см. 7.1(1).