Сопротивление поперечных сечений
(1) Сопротивление пластической деформации при сжатии Npl,Rd сталежелезобетонного сечения должно рассчитываться посредством сложения пластических сопротивлений его компонентов:
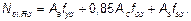 (6.30)
(6.30)
Выражение (6.30) применяется к стальному профилю в полной и частичной бетонной оболочке. Для сечений, заполненных бетоном, вместо коэффициента 0,85 должен использоваться коэффициент 1,0.
(2) Сопротивление поперечного сечения совместному воздействию сжатия и изгиба, а также соответствующая кривая взаимодействия могут рассчитываться с помощью прямоугольных эпюр напряжений (см. рисунок 6.18), с принятием расчетной силы сдвига VEd согласно (3). Прочность бетона на растяжение не должна учитываться.
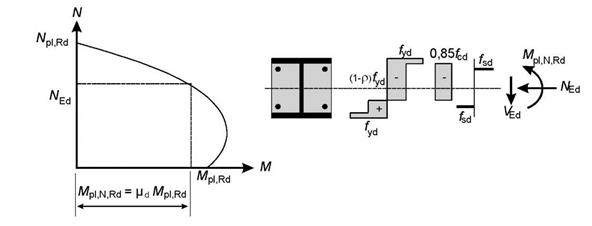
Рисунок 6.18 — Кривая взаимодействия для совместного сжатия и одноосного изгиба
(3) Влияние поперечных сдвигающих сил на сопротивление изгибу и воздействию нормальной силы должно учитываться во время расчета кривой взаимодействия, если сила сдвига Va,Ed на стальное сечение превышает 50 % расчетного сопротивления сдвигу Vpl,a,Rd стального сечения (см. 6.2.2.2).
Если Va,Ed > Vpl,a,Rd, влияние поперечного сдвига на сопротивление при совместном изгибе и сжатии должно учитываться посредством использования уменьшенной расчетной прочности стали (1 – r) fyd
в области сдвига Av согласно 6.2.2.4 (2) и рисунку 6.18.
Сдвигающая сила Va,Ed не должна превышать сопротивление сдвигу стального профиля, определенное согласно 6.2.2. Сопротивление сдвигу Vс,Ed железобетонной части должно проверяться согласно EN 1992-1-1:2004, 6.2.
(4) Если не используется более точный метод, величина VEd может быть разделена на величину Va,Ed, воздействующую на конструкционную сталь, и величину Vс,Ed, воздействующую на железобетонное сечение:
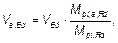 (6.31)
(6.31)
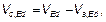 (6.32)
(6.32)
где Mpl,a,Rd — пластический предельный момент стального сечения;
Mpl,Rd — пластический предельный момент сталежелезобетонного сечения.
Для упрощения можно допустить, что VEd воздействует только на сечение из конструкционной стали.
(5) В целях упрощения, кривую взаимодействия можно заменить многоугольной диаграммой (сплошная линия на рисунке 6.19). На рисунке 6.19 в качестве примера показано распределение пластического напряжения полностью заключенного в оболочку сечения для точек от А до D. При этом величина Npm,Rd должна приниматься как 0,85fcdAc — для сечений в полной и частичной бетонной оболочке (см. рисунок 6.17а–с) и как fedAc — для сечений, заполненных бетоном (см. рисунок 6.17d–f).
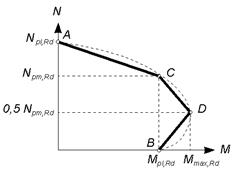
Рисунок 6.19, лист 1 — Упрощенная кривая взаимодействия
И соответствующие распределения напряжений
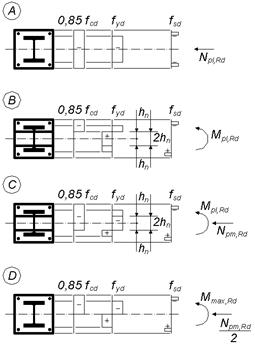
Рисунок 6.19, лист 2
(6) Для труб круглого сечения, заполненных бетоном, может учитываться повышение прочности бетона за счет его ограничения при условии, что относительная гибкость 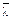 (см. 6.7.3.3) не превышает 0,5, а e/d < 0,1, где е является эксцентриситетом нагружения, равным Med /NEd, а d является внешним диаметром стойки. Исходя из этого, пластическое сопротивление сжатию можно определить
(см. 6.7.3.3) не превышает 0,5, а e/d < 0,1, где е является эксцентриситетом нагружения, равным Med /NEd, а d является внешним диаметром стойки. Исходя из этого, пластическое сопротивление сжатию можно определить
по следующему выражению:
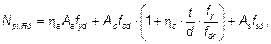 (6.33)
(6.33)
где t — толщина стенки стальной трубы.
Для элементов с е = 0 значения hа = hао и hс = hсо определяют по формулам:
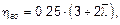 при этом hао £ 1,0; (6.34)
при этом hао £ 1,0; (6.34)
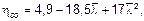 при этом hсо ³ 0, (6.35)
при этом hсо ³ 0, (6.35)
Для элементов, подвергающихся совместному воздействию сжатия и изгиба при 0 < e/d £ 0,1, значения hа и hс должны определяться согласно формулам (6.36) и (6.37), где hао и hсо определяют по формулам (6.34) и (6.35):
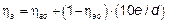 (6.36)
(6.36)
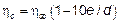 (6.37)
(6.37)
Для e/d > 0,1 hа = 1,0, а hс = 0.
