Эпюр 2. пересечение многогранных поверхностей
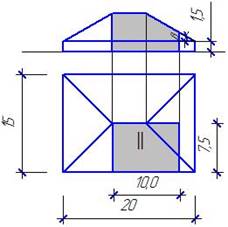
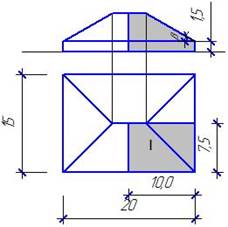
Схема здания с вырезом I Схема здания с вырезом II
Содержание эпюра
Дана схема здания размером в плане 20м´15м с четырехскатной кровлей, угол наклона которой к горизонтальной плоскости проекций равен b.
Требуется:
1. Начертить вырез здания (10м´7,5 м) в масштабе 1:100, расположив его под углом a к фронтальной плоскости.
2. Взять точку S на расстоянии (по высоте) 5 м от середины плоскости ската Р. Построить правильную пирамиду, используя точку S как ее вершину. Основание пирамиды (квадратное или треугольное) должно лежать на горизонтальной плоскости проекций. Уклон ребер пирамиды составляет 2:1 (высота пирамиды относиться к горизонтальной проекции ребра, как 2:1). Одна сторона основания должна быть параллельна стороне выреза здания.
3. Построить пересечение пирамиды и выреза здания.
4. Построить следы плоскостей скатов кровли (Р и Q).
5. Способом замены плоскостей проекций определить натуральную величину одного из скатов кровли.
6. Построить тени от пирамиды и здания на горизонтальной и фронтальной плоскостях проекций.
7. Построить аксонометрию с тенями.
ПОЯСНЕНИЯ К ВЫПОЛНЕНИЮ ЭПЮРА 2
Задача 1. Начертить вырез здания (10х7,5 м) в масштабе 1:100, расположив его под углом a к фронтальной плоскости.
Для этого берем на горизонтальной оси произвольную точку и под заданным углом a вычерчиваем прямоугольный вырез здания. Используя размеры отрезка b и с заданной схемы здания, наносим линию ската (рис.10).
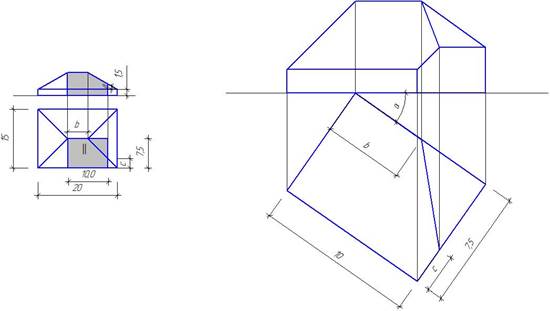
Рис.10. Вычерчивание выреза здания в М 1:100
Задача 2. Взять точку S на расстоянии (по высоте) 5 м от середины плоскости ската Р. Построить правильную пирамиду, используя точку S как ее вершину. Основание пирамиды (квадратное или треугольное) должно лежать на горизонтальной плоскости проекций. Уклон ребер пирамиды составляет 2:1 (высота пирамиды относиться к горизонтальной проекции ребра, как 2:1).
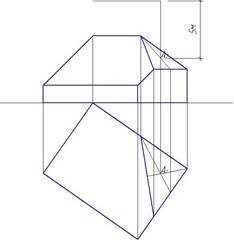
Находим середину плоскости ската с помощью медиан (рис. 11). Точка А – геометрический центр треугольника. От точки А2 вверх откладываем 5 м (в М1:100 это будет 5 см).
Теперь необходимо построить правильную пирамиду, используя полученную высоту (рис. 12).
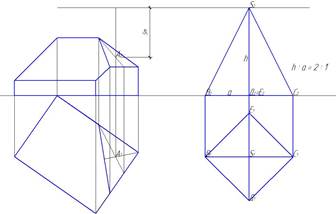
Рис. 11. Построение высоты пирамиды
Рис. 12. Построение правильной пирамиды
Задача 3. Построить пересечение пирамиды и выреза здания.
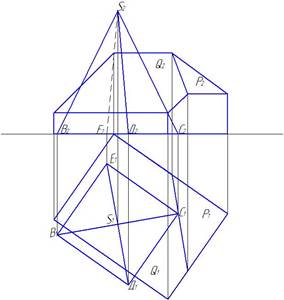
Располагаем пирамиду так, чтобы одна из сторон основания была параллельна стороне здания, а одна из точек основания пирамиды находилась на линии ската (рис. 13).
Рис. 13. Совмещение пирамиды и выреза здания
Теперь необходимо построить точки пересечения ребер пирамиды со скатом Q и точки пересечения линии карниза здания с гранями пирамиды ВSЕ и ДSС. Для того, чтобы найти точку пересечения линии карниза здания с гранью пирамиды ВSЕ, нужно задать через линию карниза секущую плоскость g (рис. 14).
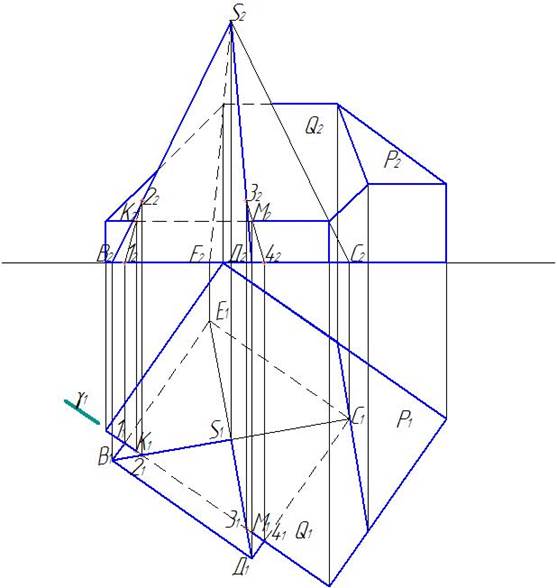
Рис. 14. Нахождение точек пересечения линии карниза здания с гранями пирамиды
Решение сводится к первой позиционной задаче – к нахождению точки пересечения прямой (в данном случае это линия карниза) и плоскости (сначала это грань пирамиды ВSЕ, а затем ДSС).
На горизонтальной плоскости проекций отмечаем точку 11 на стороне основания пирамиды ВЕ и точку 21 на ребре SB. На фронтальной плоскости проекций находим соответствующие этим точкам фронтальные проекции 12 и 22. Соединяем точки 12 и 22 прямой, которая пересечет линию карниза в точке К2. По проекционной линии находим горизонтальную проекцию этой точки – К1. Аналогичным образом находим точки М2 и М1.
Далее находим проекции точки пересечения ребра ЕS c плоскостью Q – скатом крыши здания (рис.15).
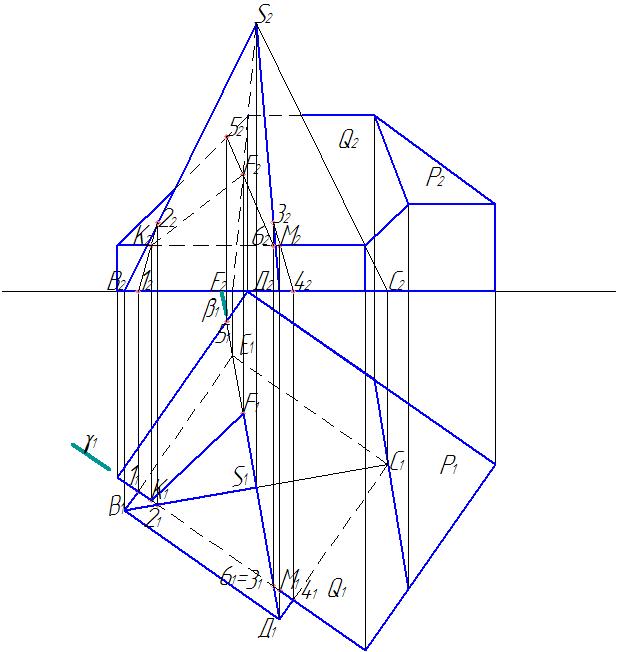
Рис. 15. Нахождение точки пересечения ребра пирамиды SЕ и ската крыши Q
И снова решаем первую позиционную задачу. Через ребро Е1S1 зададим проецирующую плоскость b1, найдем точки пересечения проекции этой плоскости со скатом Q1 . Это будут точки 51 и 61. Находим их фронтальные проекции 52 и 62. Соединяем их прямой линией и отмечаем точку F2 – точку пересечения этой линии с фронтальной проекцией ребра S2Е2. Находим горизонтальную проекцию этой точки – F1. Точки К1 и F1, К2 и F2 соединяем, учитывая видимость.
Таким же способом находим горизонтальную и фронтальную проекции точки пересечения ребра СS с плоскостью ската Q - это точки N2 и N1 (рис. 16).
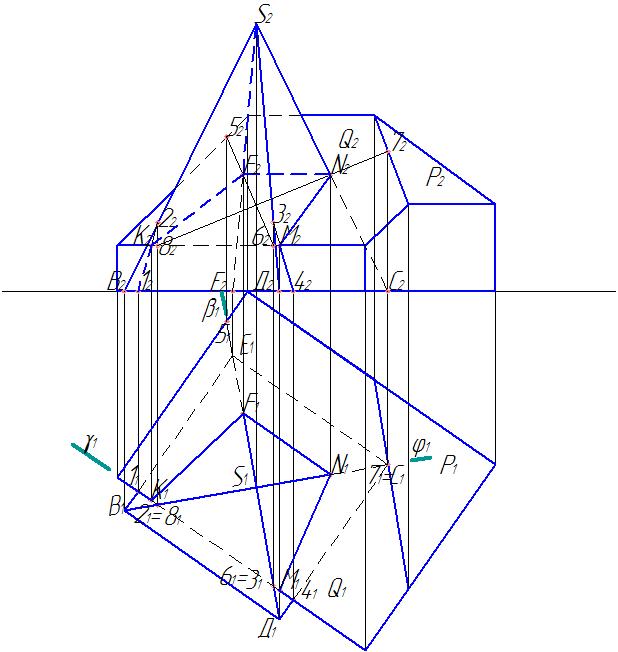
Рис. 16. Нахождение точки пересечения ребра пирамиды SC и ската крыши Q
Горизонтальные и фронтальные проекции точек К, F, N, М соединяем, учитывая видимость. Необходимо также соединить точку М2 с 42 и точку К2 с точкой 12. Это проекции врезки граней пирамиды и вертикальной стены выреза здания.
Задача 4. Построить следы плоскостей скатов кровли (Р и Q).
Строить следы начинаем с горизонтальной проекции ската Р. Линию раздела скатов 91 101 продолжаем до пересечения с осью Х, получаем точку А1 . На продолжении линии раздела скатов 92 102 находим фронтальную проекцию точки А2. Теперь продолжаем фронтальную проекцию 92 102 до пересечения с осью Х, где получим точку L2. По проекционной связи находим горизонтальную проекцию точки L1 (рис. 17)..
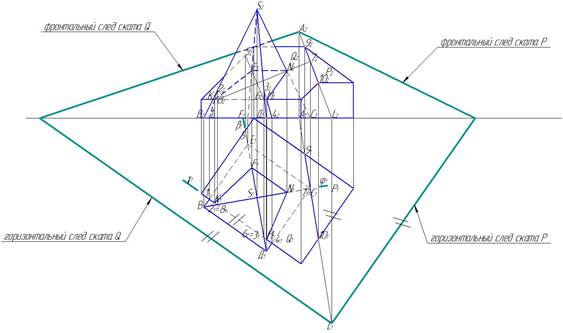
Рис. 17. Построение следов скатов Q и Р.
Горизонтальный след ската Р будет параллелен стороне этого ската, а горизонтальный след ската Q – параллелен стороне ската Q. Доводим горизонтальные следы до пересечения с осью Х, а затем эти точки соединяем с точкой А2. Следы построены.
Задача 5. Способом замены плоскостей проекций определить натуральную величину одного из скатов кровли.
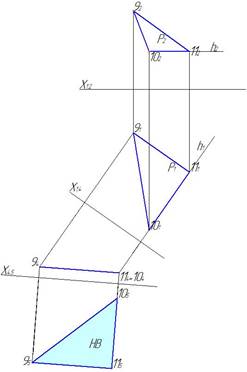
Лучше всего вынести проекции ската Р на свободное поле чертежа или на новом листе и решить задачу нахождения натуральной величины ската, сделав две замены плоскостей (рис.18). Сначала перпендикулярно горизонтали вводят плоскость П4 и плоскость Р1 превращают во фронтально-проецирующую плоскость, а затем к проекции 94 104 проводят параллельно новую горизонтальную плоскость П5.
Рис. 18. Нахождение натуральной величины плоскости Р
