Архитектура персептрона

НЕЙРОННЫЕ СЕТИ

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.. 3

1. ПЕРСЕПТРОНЫ... 4

1.1. Архитектура персептрона. 4

1.2. Алгоритм обучения персептрона. 7

1.3. Создание персептрона. 8

1.4. Моделирование работы персептрона. 10

1.5. Адаптация персептрона. 11

1.6. Задания. 14

2. МНОГОСЛОЙНЫЙ ПЕРСЕПТРОН.. 15

2.1. Архитектура многослойного персептрона. 15

2.2. Распознавание образов. 16

2.2.1. Использование Neural Network Pattern Recognition Tool 16

2.2.2. Задания. 27

2.2.3. Использование команд. 27

2.2.4. Задания. 31

2.2.5. Распознавание букв латинского алфавита. 32

2.2.6. Задания. 37

2.3. Аппроксимация функций. 38

2.3.1. Использование Neural Network Fitting Tool 38

2.3.2. Задания. 48

2.3.3. Использование команд. 48

2.3.4. Задания. 54

3. СЕТИ И КАРТЫ КОХОНЕНА.. 55

3.1. Сети Кохонена. 55

3.1.1. Архитектура сетей Кохонена. 55

3.1.2. Правило обучения сети Кохонена. 56

3.1.3. Создание сети Кохонена. 58

3.1.4. Обучение сети Кохонена. 58

3.1.5. Задания. 60

3.2. Карты Кохонена. 61

3.2.1. Архитектура и обучение карт Кохонена. 61

3.2.2. Кластеризация с использованием Neural Network Clustering Tool 62

3.2.3. Задания. 71

3.2.4. Использование команд. 71

3.2.5. Задания. 74

4. РАДИАЛЬНЫЕ БАЗИСНЫЕ СЕТИ.. 75

4.2. Архитектура сети. 76

4.3. Создание сети. 77

4.3.1. Построение сети с числом нейронов, равным числу обучающих примеров. 77

4.3.2. Итерационная процедура формирования сети. 80

4.4. Задания. 82

5. СЕТИ ХОПФИЛДА.. 83

5.1. Архитектура сети. 83

5.2. Создание сети. 85

5.3. Задания. 90

6. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ... 90

6.1. Методические указания. 90

6.2. Варианты заданий. 94

ЛИТЕРАТУРА.. 97

ВВЕДЕНИЕ

Лабораторный практикум посвящен моделированию основных видов нейронных сетей в пакете Neural Networks Toolbox системы MATLAB. Лабораторные работы предусматривают работы как с использованием стандартных инструментов с графическим инструментом, так и использование разработанной авторами библиотеки программ. Каждая лабораторная работа содержит задания для самостоятельной работы.

Представлен также набор заданий для индивидуальной самостоятельной работы. Особенностью индивидуальных заданий является использование реальных данные по прикладным задачам в области биологии, медицины, физики, техники, социологии, представленных в репозитории UCI (UCI Machine Learning Repository http://mlr.cs.umass.edu/ml/) университета г. Ирвайн (Калифорния, США).

ПЕРСЕПТРОНЫ

Архитектура персептрона

Цель занятия – изучение принципов построения и обучения персептрона.

Персептрон – это однослойная нейронная сеть, построенная на основе модели МакКаллока‑Питса [1 – 3]. Структура нейрона персептрона в обозначениях пакета Neural Networks Toolbox (NNT) системы MATLAB имеет вид рис. 1.1. Следует отметить, что персептронами часто называют и многослойные сети.

Рис. 1.1. Структура нейрона персептрона

В персептроне используется пороговая (ступенчатая) функция активации hardlimс жесткими ограничениями

Используется также симметричная ступенчатая функция активации с жесткими ограничениями hardlims

Ступенчатые функции активации позволяют нейрону персептрона осуществлять линейное разделение пространства входных сигналов на два класса. Поэтому персептрон используется для решения задач классификации. В случае двух входных сигналов на выходе адаптивного сумматора имеем

.

При использовании функции активации разделяющая линия делит плоскость на две области:

Например, для уравнение разделяющей линии имеет вид рис. 1.2

.

В полуплоскости, расположенной по направлению вектора весов , выход нейрона равен 1. На разделительной линии выход равен 1. В полуплоскости, расположенной в направлении, противоположном направлению вектора , выход равен 0. В трехмерном случае границей раздела будет плоскость, в многомерном случае – гиперплоскость.

Рис. 1.2. Пример разделяющей линии

Задача классификации может быть решена с помощью единственного нейрона только в том случае, если входные сигналы являются линейно разделимыми. Например, в случае двух входных сигналов персептрон не может реализовать функцию исключающего ИЛИ (XOR), описываемую таблицей 1.1

Таблица 1.1. Таблица истинности для функции исключающего ИЛИ

В этом случае невозможно провести линию, разделяющую пространство данных на два подпространства, в одно из которых входили бы векторы (0,1) и (1,0), а в другое – векторы (0,0) и (1,1) см. рис. 1.3.

Рис. 1.3. К проблеме исключающего ИЛИ

Однослойная сеть – персептрон [2], построенная из рассмотренных нейронов в обозначениях NNT в развернутом и укрупненном виде представлена на рис. 1.4.

Рис. 1.4. Структура персептрона

В такой сети каждый нейрон производит свое линейное разделение входных векторов. Выход j‑го нейрона равен

,

где – вес 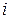‑го входа нейрона , – 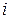‑й компонент входного вектора, – выход адаптивного сумматора ‑го нейрона, – функция активации

или

Смещение формально рассматривается как единичный вход с весом . Совокупность весовых коэффициентов сети можно представить в виде матрицы

,

где – коэффициент связи между i‑ым нейроном и j‑входом.

Каждая строка матрицы представляет собой вектор-строку весов соответствующего нейрона. В матричной форме персептрон описывается выражением

,

где – вектор выхода сети, – вектор-функция активации, – вектор входов.