Распознавание букв латинского алфавита
Требуется создать нейронную сеть для распознавания 26 букв латинского алфавита [1]. Будем считать, что имеется система считывания символов, которая каждый символ представляет в виде матрицы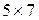 
. Например, символ A может быть представлен, как показано на рис. 2.22.
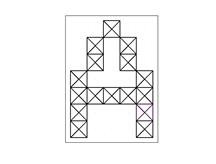
Рис. 2.22. Представление символа
Реальная система считывания символов работает не идеально, а сами символы отличаются по начертанию. Поэтому, например, для символа A единицы могут располагаться не в тех клетках, как показано на рис. 2.22. Кроме того, вне контура символа могут возникать ненулевые значения. Клетки, соответствующие контуру символа, могут содержать значения, отличные от 1. Будем называть все искажения шумом.
В MATLAB имеется функция prprob, возвращающая матрицу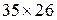 
, каждый столбец которой представляет записанную в виде вектора матрицу 
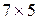, описывающую соответствующую букву (первый столбец описывает букву A, второй — букву B и т. д.). Функция prprob возвращает также целевую матрицу размером 
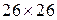, каждый столбец которой содержит одну единицу в строке, соответствующей номеру буквы при нулевых остальных элементах столбца. Например, первый столбец, соответствующий букве A, содержит 1 в первой строке.
Пример. Определим шаблон для буквы A (программа Template_A.m).
% Пример формирования шаблона для буквы A
[alphabet, target] = prprob;
i=1; % номер буквы A
v=alphabet(:,i); % вектор, соответствующий букве A
template=reshape(v, 5,7)';
template
plotchar(v);
Кроме уже описанной функции prprob в программе использованы функции reshape, которая формирует матрицу 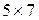, а после транспонирования — 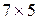(убедитесь, что невозможно сразу сформировать матрицу 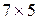), и функция plotchar, которая рисует 35 элементов вектора в виде решетки 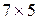. После выполнения программы Template_A.m получим матрицу template и шаблон буквы A, как показано на рис. 2.23.
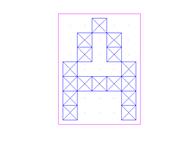
Рис. 2.23. Сформированный шаблон буквы A
Для распознавания букв латинского алфавита необходимо построить нейронную сеть с 35 входами и 26 нейронами в выходном слое. Примем число нейронов скрытого слоя равным 10 (такое число нейронов выбрано экспериментально). Если при обучении возникнут затруднения, то можно увеличить количество нейронов этого уровня.
Сеть распознавания образов строится функцией patternnet.Обратите внимание, что при создании сети не задается число нейронов входного и выходного слоев. Эти параметры неявно задаются при обучении сети.
Рассмотрим программу распознавания букв латинского алфавита Char_recognition.m
% Программа распознавания букв латинского алфавита
clc
clear all
close all
[alphabet, targets] = prprob; % Формирование входных и целевых векторов
[R,Q]=size(alphabet);
[S2,Q]=size(targets);
% Создание сети
net=patternnet;
% Обучение сети в отсутствие шума
P = alphabet;
T = targets;
[net,tr] = train(net,P,T);
disp('Обучение сети в отсутствие шума завершено. Нажмите Enter');
pause;
% Обучение в присутствии шума
netn = net; % сохранение обученной сети
T = [targets targets targets targets];
for pass = 1:10
P = [alphabet, alphabet, ...
(alphabet + randn(R,Q)*0.1), ...
(alphabet + randn(R,Q)*0.2)];
[netn,tr] = train(netn,P,T);
end
disp('Обучение сети в присутствии шума завершено. Нажмите Enter');
pause;
% Повторное обучение в отсутствии шума
[netn,tr] = train(netn,P,T);
disp('Повторное обучение сети в отсутствии шума завершено. Нажмите Enter');
pause;
% Тестирование сети
noise_rage=0:0.05:0.5; % Массив уровней шума (стандартных отклонений шума
max_test=10;
network1=[];
network2=[];
T=targets;
% Выполнение теста для каждого уровня шума
for noiselevel=noise_rage
errors1=0;
errors2=0;
for i=1:max_test
P=alphabet+randn(35, 26)*noiselevel;
% Тест для сети 1
A=net(P);
AA=compet(A);
errors1=errors1+sum(sum(abs(AA-T)))/2;
% Тест для сети 2
An=netn(P);
AAn=compet(An);
errors2=errors2+sum(sum(abs(AAn-T)))/2;
end
% Средние значения ошибок (max_test последовательностей из 26 векторов целей)
network1=[network1 errors1/26/max_test];
network2=[network2 errors2/26/max_test];
end
plot(noise_rage, network1*100, noise_rage, network2*100);
grid on;
title('Погрешность сети');
xlabel('Уровень шума');
ylabel('Процент ошибки');
legend('Идеальные входные векторы','Зашумленные входные векторы');
disp('Тестирование завершено');
Оператор [alphabet, targets] = prprob; формируют массив векторов входа alphabet размера 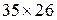с шаблонами символов алфавита и массив целевых векторов targets.
Сеть создается оператором net=patternnet.Примем параметры сети по умолчанию. Обучение сети производится сначала в отсутствии шума. Затем сеть обучается на 10 наборах идеальных и зашумленных векторов. Два набора идеальных векторов используются, чтобы сеть сохранила способность классифицировать идеальные векторы (без шума). После обучения сеть "забыла", как классифицировать некоторые векторы, свободные от шума. Поэтому сеть следует снова обучить на идеальных векторах.
Следующий фрагмент программы производит обучение в отсутствие шума:
% Обучение сети в отсутствие шума
P = alphabet;
T = targets;
[net,tr] = train(net,P,T);
disp('Обучение сети в отсутствие шума завершено. Нажмите Enter');
pause;
Обучение в присутствии шума проводится с применением двух идеальных и двух зашумленных копий входных векторов. Шум имитировался псевдослучайными нормально распределенными числами с нулевым средним значением и стандартным отклонением 0.1 и 0.2. Обучение в присутствии шума производит следующий фрагмент программы:
% Обучение в присутствии шума
netn = net; % сохранение обученной сети
T = [targets targets targets targets];
for pass = 1:10
P = [alphabet, alphabet, ...
(alphabet + randn(R,Q)*0.1), ...
(alphabet + randn(R,Q)*0.2)];
[netn,tr] = train(netn,P,T);
end
disp('Обучение сети в присутствии шума завершено. Нажмите Enter');
pause;
Поскольку сеть обучалась в присутствии шума, то имеет смысл повторить обучение без шума, чтобы гарантировать правильную классификацию идеальных векторов:
% Повторное обучение в отсутствии шума
[netn,tr] = train(netn,P,T);
disp('Повторное обучение сети в отсутствии шума завершено. Нажмите Enter');
pause;
Тестирование сети проводилось для двух структур сети: сети 1, обученной на идеальных векторах, и сети 2, обученной на зашумленных последовательностях. Шум со средним значением 0 и стандартным отклонением от 0 до 0.5 с шагом 0.05 добавлялся к векторам входа. Для каждого уровня шума формировалось 10 зашумленных векторов для каждого символа, и вычислялся выход сети (желательно увеличить число зашумленных векторов, но это заметно увеличит время работы программы). Сеть обучается так, чтобы сформировать единицу в единственном элементе выходного вектора, позиция которого соответствует номеру распознанной буквы, и заполнить остальную часть вектора нулями. Никогда на выходе сети не будет формировать вектор выхода, состоящий точно из 1 и 0. Поэтому в условиях действия шумов выходной вектор обрабатывается функцией compet, которая преобразует выходной вектор так, что самый большой выходной сигнал получает значение 1, а все другие выходные сигналы получают значение 0.
Соответствующий фрагмент программы имеет вид:
% Выполнение теста для каждого уровня шума
for noiselevel=noise_rage
errors1=0;
errors2=0;
for i=1:max_test
P=alphabet+randn(35, 26)*noiselevel;
% Тест для сети 1
A=net(P);
AA=compet(A);
errors1=errors1+sum(sum(abs(AA-T)))/2;
% Тест для сети 2
An=netn(P);
AAn=compet(An);
errors2=errors2+sum(sum(abs(AAn-T)))/2;
end
% Средние значения ошибок (max_test последовательностей из 26 векторов целей)
network1=[network1 errors1/26/max_test];
network2=[network2 errors2/26/max_test];
end
plot(noise_rage, network1*100, noise_rage, network2*100);
grid on;
title('Погрешность сети');
xlabel('Уровень шума');
ylabel('Процент ошибки');
legend('Идеальные входные векторы','Зашумленные входные векторы');
disp('Тестирование завершено');
При вычислении погрешности распознавания, например, errors1=errors1+sum(sum(abs(AA-T)))/2, учтено, что при неправильном распознавании не совпадают два элемента выходного вектора и вектора цели, поэтому при подсчете погрешности производится деление на 2. Сумма sum(abs(AA-T)) вычисляет число не совпавших элементов для одного примера. Сумма sum(sum(abs(AA-T))) вычисляет число не совпавших элементов по всем примерам.
Графики погрешности распознавания сетью, обученной на идеальных входных векторах, и сетью, обученной на зашумленных векторах, представлены на рис. 2.24. Из рис. 2.24 видно, что сеть, обученная на зашумленных образах, дает небольшую погрешность, а на идеальных входных векторах сеть обучить не удалось.
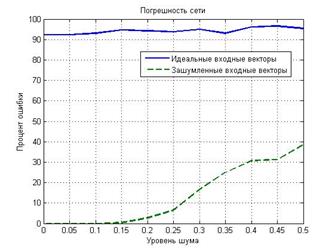
Рис. 2.24. Погрешности сети в зависимости от уровня шума
Проверим работу обученной сети (в рабочем пространстве MATLAB должна присутствовать обученная сеть). Программа Recognition_J.m формирует зашумленный вектор для буквы J и распознает букву. Функция randn формирует псевдослучайное число, распределенное по нормальному закону с нулевым математическим ожиданием и единичным среднеквадратичным отклонением. Случайное число с математическим ожиданием m и среднеквадратическим отклонением d получается по формуле m+randn*d(в программеm=0, d=0.2).
noisyJ = alphabet(:,10)+randn(35,1) * 0.2;
plotchar(noisyJ);
disp('Зашумленный символ. Нажмите Enter');
pause;
A2 = netn(noisyJ);
A2 = compet(A2);
ns = find(A2 == 1);
disp('Распознан символ');
ns
plotchar(alphabet(:,ns));
Программа выводит номер распознанной буквы, зашумленный шаблон буквы (рис. 2.25) и шаблон распознанной буквы (2.26).
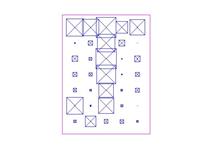
Рис. 2.25. Зашумленный шаблон буквы
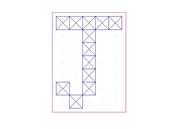
Рис. 2.26. Шаблон распознанной буквы
Таким образом, рассмотренные программы демонстрируют принципы распознавания изображений с помощью нейронных сетей. Обучение сети на различных наборах зашумленных данных позволило обучить сеть работать с изображениями, искаженными шумами.
Задания
1. Проделайте все приведенные примеры.
2. Испытайте распознавание различных букв
3. Исследуйте влияние шума в программах на точность распознавания символов.
Аппроксимация функций