Установления корреляционных градуировочных зависимостей
При проведении инструментального обследования строительных конструкций зданий и сооружений часто возникает задача оценки аналитического вида зависимости измеряемых параметров от различных косвенных характеристик или во времени. Например: зависимость скорости роста трещин от времени, глубина просачивания агрессивной среды внутрь конструкции от времени или прочность бетона от скорости прохождения ультразвука через его структуру. Аналитические зависимости позволяют прогнозировать изменение анализируемых характеристик на различный период времени, а также использовать косвенные характеристики для оценки механических характеристик строительных материалов.
Вид аналитической зависимости на основе результатов экспериментальных исследований устанавливается с помощью методов корреляционного и регрессионного анализа.
Чаще всего приходится иметь дело с линейными зависимостями вида
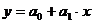 , (6.9)
, (6.9)
где y - измеряемая косвенная характеристика; x - механическая характеристика материала.
Коэффициенты уравнения регрессии a0 и a1 рассчитывают по формулам
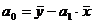 (6.10)
(6.10)
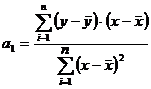 , (6.11)
, (6.11)
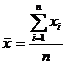 , (6.12)
, (6.12)
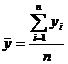 , (6.13)
, (6.13)
где yi – механическая характеристика материала; xi – косвенная харак-теристика; n – объем выборки.
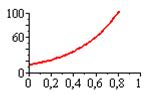
В некоторых случаях зависимость может оказаться нелинейной. В этих случаях коэффициенты нелинейных уравнений регрессии могут быть найдены преобразованием исходных значений x,y к линейному масштабу xc,yc. Для преобразованных значений xc,yc находят коэффициенты линейной регрессии a0,a1. Коэффициенты нелинейного уравнения регрессии b0,b1 находятся путем соответствующих преобразований линейных коэффициентов a0,a1. Способы преобразования коэффициентов для некоторых аналитических зависимостей приведены в табл. 6.3.
Таблица 6.3
Преобразования для построения нелинейных уравнений регрессии
| Аналитический вид зависимости | Вид функции | Способ приведения к линейной | Коэффициенты уравнения регрессии |
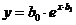 | 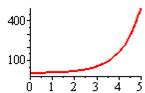 | 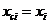 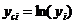 | 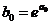 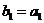 |
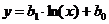 |  | 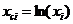 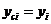 | 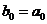 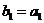 |
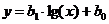 |  | 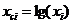 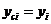 | 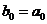 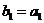 |
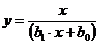 | 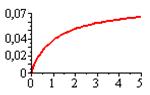 | 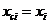 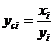 | 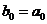 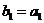 |
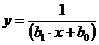 |  | 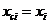 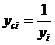 | 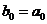 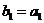 |
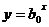 |  | 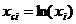 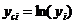 | 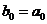 |
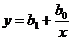 |  | 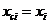 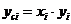 | 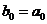 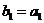 |
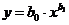 |  | 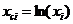 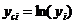 | 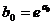 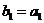 |
Одной из характеристик качества полученной аналитической зависимости является коэффициент корреляции rxy. Коэффициент корреляции изменяется в пределах 0…1. Чем ближе коэффициент корреляции к единице, тем точнее аналитическая зависимость описывает связь косвенной характеристики с механической.

Рис. 6.1. Изменение коэффициента корреляции
Коэффициент корреляции определяется для линейной зависимости по формуле
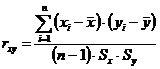 , (6.14)
, (6.14)
где Sx, Sy – среднее квадратическое отклонение x и у соответственно.
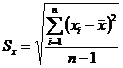 , (6.15)
, (6.15)
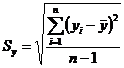 . (6.16)
. (6.16)
Построенная аналитическая зависимость, рекомендуется к применению, если ее коэффициент корреляции не менее 0,7. Качественная характеристика величины коэффициента корреляции представлена в табл.6.4.
Таблица 6.4
Качественная характеристика корреляционной зависимости
| Коэффициент корреляции, rxy | Качественная характеристика корреляции |
| 0,1..0,3 | Слабая |
| 0,3..0,5 | Умеренная |
| 0,5..0,7 | Заметная |
| 0,7..0,9 | Высокая |
| 0,9..1,0 | Очень высокая |
После установления аналитического вида зависимости проводят ее корректировку путем отбраковки отличающихся единичных результатов испытаний. Результаты испытаний исключаются из общей выборки значений для построения зависимости, если они не удовлетворяют условию
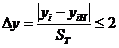 , (6.17)
, (6.17)
где yiH – косвенная характеристика, определенная по установленной градуировочной зависимости; ST – остаточное среднее квадратическое отклонение
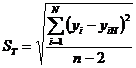 . (6.18)
. (6.18)
После отбраковки некоторых единичных результатов из общей выборки, аналитический вид зависимости устанавливают заново.
Погрешность определения механической характеристики материала по установленной аналитической зависимости определяют по формуле:
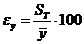 % (6.19)
% (6.19)
Использование установленной зависимости для определения механических характеристик материалов допускается только в том случае, если ее погрешность εy <12 %.
Пример: Прочность бетона проектного класса B20 контролируют методом отскока прибором КМ. Требуется установить зависимость прочности бетона (МПа) от величины отскока (мм) и оценить ее погрешность. Для установления зависимость между величиной отскока и прочностью бетона были изготовлены и испытаны 11 серий образцов. Прочность бетона представлена выборкой y, соответствующая величина отскока представлена выборкой x. Результаты измерений представлены в столбцах x,y табл. 6.5.
Таблица 6.5
Результаты измерений
| № измерения | Отскок x, мм | Прочность y, МПа | 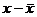 | 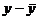 | 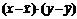 | 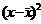 | 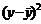 |
| 18,6 | 26,7 | 0,67 | 3,33 | 2,24 | 0,45 | 11,07 | |
| 17,8 | 24,0 | -0,13 | 0,63 | -0,08 | 0,02 | 0,39 | |
| 18,1 | 23,6 | 0,17 | 0,23 | 0,04 | 0,03 | 0,05 | |
| 16,0 | 16,0 | -1,93 | -7,37 | 14,21 | 3,71 | 54,36 | |
| 19,2 | 27,6 | 1,27 | 4,23 | 5,38 | 1,62 | 17,87 | |
| 18,8 | 26,5 | 0,87 | 3,13 | 2,73 | 0,76 | 9,78 | |
| 17,8 | 22,2 | -0,13 | -1,17 | 0,15 | 0,02 | 1,38 | |
| 16,4 | 18,4 | -1,53 | -4,97 | 7,59 | 2,33 | 24,73 | |
| 18,4 | 24,9 | 0,47 | 1,53 | 0,72 | 0,22 | 2,33 | |
| 18,8 | 26,2 | 0,87 | 2,83 | 2,47 | 0,76 | 7,99 | |
| 17,3 | 21,0 | -0,63 | -2,37 | 1,49 | 0,39 | 5,63 | |
| Σ=36,94 | Σ=10,32 | Σ=135,58 |
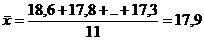 ;
; 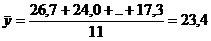 ;
;
 ;
; 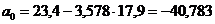 ;
;
аналитический вид корреляционной зависимости: y=-40,783+3,578·x;
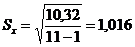 ;
; 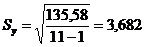 ;
;
коэффициент корреляции установленной зависимости: 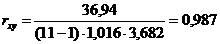
по табл.6.4 корреляция “очень высокая”.
Выполним оценку погрешности установленной аналитической, градуировочной зависимости. Для этого составим вспомогательную табл. 6.6.
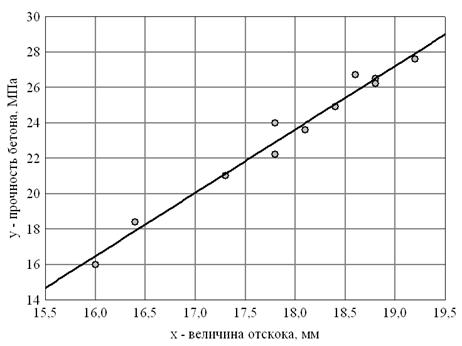
Рис. 6.2. Зависимость прочности бетона от величины отскока
Таблица 6.6.
Вспомогательная таблица для оценки погрешности установленной аналитической зависимости
| № | Отскок x, мм | Фактическая прочность y, МПа | Прочность по зависимости yh, МПа | 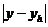 | 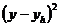 | 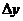 <2 <2 |
| 18,6 | 26,7 | 25,78 | 0,92 | 0,85 | 1,23 | |
| Окончание табл. 6.6 | ||||||
| № | Отскок x, мм | Фактическая прочность y, МПа | Прочность по зависимости yh, МПа | 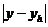 | 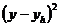 |  <2 <2 |
| 17,8 | 24,0 | 22,92 | 1,08 | 1,17 | 1,45 | |
| 18,1 | 23,6 | 23,99 | 0,39 | 0,15 | 0,52 | |
| 16,0 | 16,0 | 16,48 | 0,48 | 0,23 | 0,64 | |
| 19,2 | 27,6 | 27,93 | 0,33 | 0,11 | 0,44 | |
| 18,8 | 26,5 | 26,50 | 0,00 | 0,00 | 0,01 | |
| 17,8 | 22,2 | 22,92 | 0,72 | 0,51 | 0,96 | |
| 16,4 | 18,4 | 17,91 | 0,49 | 0,24 | 0,66 | |
| 18,4 | 24,9 | 25,06 | 0,16 | 0,03 | 0,22 | |
| 18,8 | 26,2 | 26,50 | 0,30 | 0,09 | 0,40 | |
| 17,3 | 21,0 | 21,13 | 0,13 | 0,02 | 0,17 | |
| Σ= 5,00 |
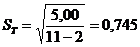 ,
,
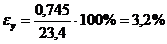 .
.
Поскольку для контроля механических характеристик материалов допускается использовать зависимости с погрешностью не более 12 %, то установленную зависимость можно использовать для контроля прочности бетона классов B20.
Пример: Требуется установить коэффициенты экспоненциальной корреляционной зависимости скорости распространения ультразвука от прочности бетона в условиях твердения. Прочность бетона представлена выборкой y, соответствующая величина скорости ультразвука выборкой x. Результаты измерений представлены в столбцах x,y табл. 6.7.
Поскольку зависимость экспоненциальная, то преобразуем результаты измерений к линейному виду по формулам xci=xi, yci=ln(yi) (табл.6.7).
Результаты измерений
Таблица 6.7
| № | Фактические данные | Преобразо-ванные к линейным данные | 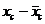 | 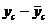 | 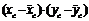 | 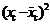 | 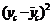 | |||||
| x, м/сек | y, МПа | xc, м/сек | yc, МПа | |||||||||
| 1,41 | 0,34 | -1047,14 | -1,53 | 1606,59 | 1096508,2 | 2,35 | ||||||
| 9,75 | 2,28 | 292,86 | 0,40 | 116,97 | 85765,31 | 0,16 | ||||||
| 13,50 | 2,60 | 567,86 | 0,72 | 411,60 | 322461,73 | 0,53 | ||||||
| 1,63 | 0,49 | -972,14 | -1,39 | 1350,57 | 945061,73 | 1,93 | ||||||
| Окончание табл. 6.7 | ||||||||||||
| № | Фактические данные | Преобразо-ванные к линейным данные | 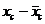 | 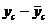 | 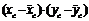 | 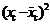 | 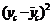 | |||||
| x, м/сек | y, МПа | xc, м/сек | yc, МПа | |||||||||
| 4,40 | 1,48 | -327,14 | -0,40 | 129,63 | 107022,45 | 0,16 | ||||||
| 11,43 | 2,44 | 432,86 | 0,56 | 241,70 | 187365,31 | 0,31 | ||||||
| 15,70 | 2,75 | 672,86 | 0,88 | 589,29 | 452736,73 | 0,77 | ||||||
| 4,15 | 1,42 | -427,14 | -0,45 | 194,24 | 182451,02 | 0,21 | ||||||
| 8,05 | 2,09 | 157,86 | 0,21 | 32,81 | 24918,88 | 0,04 | ||||||
| 18,35 | 2,91 | 772,86 | 1,03 | 797,42 | 597308,16 | 1,06 | ||||||
| 2,64 | 0,97 | -817,14 | -0,91 | 741,21 | 667722,45 | 0,82 | ||||||
| 6,05 | 1,80 | -92,14 | -0,08 | 7,17 | 8490,31 | 0,01 | ||||||
| 11,65 | 2,46 | 462,86 | 0,58 | 267,28 | 214236,73 | 0,33 | ||||||
| 9,60 | 2,26 | 322,86 | 0,38 | 123,95 | 104236,73 | 0,15 | ||||||
| Σ= 6610,43 | Σ= 4996285,71 | Σ= 8,83 | ||||||||||
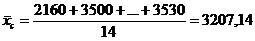 ;
; 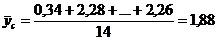 ;
;
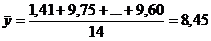 ;
;
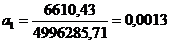 ;
; 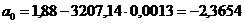 ;
;
выполняем преобразования коэффициентов линейной регрессии к экспоненциальной зависимости по формулам: 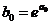 ,
, 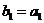 .
.
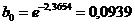 ;
; 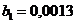 ;
;
аналитический вид корреляционной зависимости: 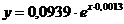 ;
;
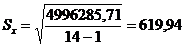 ;
; 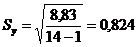 ;
;
коэффициент корреляции установленной зависимости:
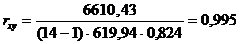
По табл.6.7 корреляция «очень высокая».
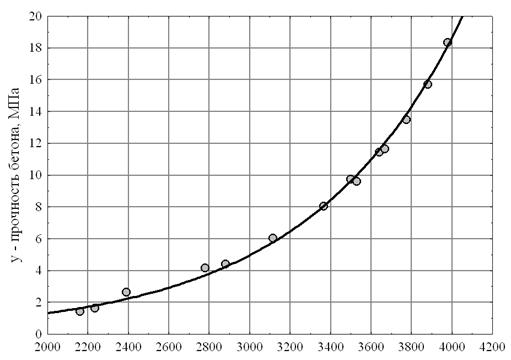
х - скорость ультразвука, м/с
Рис. 6.3. Зависимость прочности бетона от скорости ультразвука
Таблица 6.8
Оценка погрешности градуировочной зависимости
| № | Отскок x, мм | Фактическая прочность y, МПа | Прочность по зависимости yh, МПа | 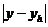 | 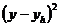 | 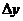 <2 <2 |
| 1,41 | 1,64 | 0,23 | 0,05 | 0,73 | ||
| 9,75 | 9,63 | 0,12 | 0,01 | 0,37 | ||
| 13,50 | 13,86 | 0,36 | 0,13 | 1,17 | ||
| 1,63 | 1,81 | 0,18 | 0,03 | 0,57 | ||
| 4,40 | 4,24 | 0,16 | 0,02 | 0,51 | ||
| 11,43 | 11,59 | 0,16 | 0,03 | 0,53 | ||
| 15,70 | 15,93 | 0,23 | 0,05 | 0,74 | ||
| 4,15 | 3,72 | 0,43 | 0,19 | 1,40 | ||
| 8,05 | 8,06 | 0,01 | 0,00 | 0,03 | ||
| 18,35 | 18,18 | 0,17 | 0,03 | 0,55 | ||
| 2,64 | 2,22 | 0,42 | 0,18 | 1,36 | ||
| 6,05 | 5,79 | 0,26 | 0,07 | 0,85 | ||
| 11,65 | 12,06 | 0,41 | 0,17 | 1,34 | ||
| 9,60 | 10,02 | 0,42 | 0,18 | 1,37 | ||
| Σ= 1,15 |
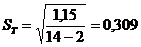 ,
,
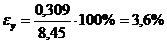 .
.
Поскольку для контроля механических характеристик материалов допускается использовать зависимости с погрешностью не более 12%, то установленную зависимость можно использовать для контроля прочности бетона.
Контрольные вопросы для самопроверки
