Расчет ожидаемых сдвижений и деформаций земной поверхности от отдельной очистной выработки

4.2.1. Сдвижения и деформации в главных сечениях мульды (рис. 8).

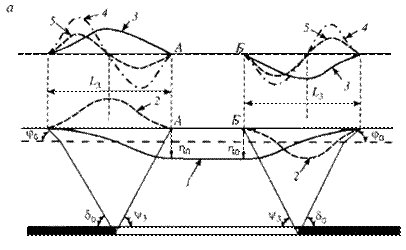
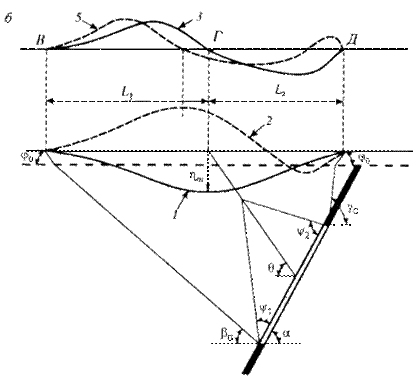
Рис. 8. Схема распределения сдвижений и деформаций в точках главных сечений мульды сдвижения при закончившемся процессе:

а - на разрезе по простиранию; б - на разрезе вкрест простирания; 1 - оседания;

2 - горизонтальные сдвижения; 3 - наклоны; 4 - кривизна; 5 - горизонтальные деформации; АБ - плоское дно; ВГ - зона обратных уступов; ГД - зона прямых уступов

Максимальное оседание земной поверхности определяется по формуле:

h_m = q₀mcosaN₁N₂, (31)

где q₀ - относительное максимальное оседание, определяемое по разд. 7 для соответствующих бассейнов и месторождений;

m - вынимаемая мощность пласта, при работе с закладкой используется эффективная мощность (п. 4.1);

a - угол падения пласта;

N₁ и N₂ - коэффициенты, определяемые по разд. 7.

Оседание земной поверхности в точках главных сечений мульды сдвижения определяется по формуле:

h_xy = h_mS(z), (32)

где S(z) - функция типовой кривой оседания, определяемая по таблицам 17-23 для соответствующих бассейнов (месторождений) в зависимости от коэффициентов N₁ - для точек главного сечения вкрест простирания пластов и N₂ - для точек главного сечения по простиранию пластов;

z_x = x/L₃ для точек, расположенных в главном сечении по простиранию пласта;

- для точек, расположенных в главном сечении вкрест простирания пласта в полумульде по падению;

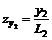- для точек, расположенных и главном сечении вкрест простирания пласта в полумульде по восстанию пласта;

x; y₁; y₂ - расстояния от точки максимального оседания (начала координат) до рассматриваемой точки, соответственно в полумульдах по простиранию, падению и восстанию;

L₁; L₂; L₃ – длины полумульд (см. рис. 8).

Наклоны в главных сечениях мульды:

а) по простиранию

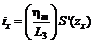; (33)

б) в сторону обратную простиранию

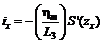; (34)

в) в полумульде по падению

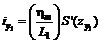; (35)

г) в полумульде по восстанию

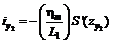, (36)

где S¢(z) - функция типовой кривой наклонов, определяемая по таблицам 17-23 для соответствующих бассейнов (месторождений), в зависимости от коэффициентов N₁ - для точек главного сечения вкрест простирания пласта и N₂ - для точек главного сечения по простиранию пласта.

Кривизна в главных сечениях мульды при a ≤ 45° определяется по формулам:

а) по простиранию

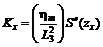; (37)

б) в полумульде по падению

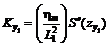; (38)

Таблица 17

Значения функций S(z), S¢(z) и S²(z) для Восточного Донбасса и месторождений Приморского края

z	N = 1	N = 0,9	N = 0,8	N ≤ 0,7
	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)
	1,00	0,0	0,0	1,00	0,0	-4,3	1,00	0,0	-7,4	1,00	0,0	-9,4
0,1	0,99	0,19	-2,1	0,98	0,47	-5,0	0,97	0,73	-7,0	0,96	0,91	-8,2
0,2	0,95	0,56	-5,1	0,90	1,02	-6,1	0,85	1,36	-5,6	0,83	1,59	-5,2
0,3	0,86	1,20	-7,3	0,77	1,61	-5,3	0,69	1,83	-3,0	0,65	1,90	-1,8
0,4	0,71	1,89	-5,7	0,58	1,98	1,8	0,48	1,91	0,7	0,46	1,85	2,3
0,5	0,50	2,20		0,39	1,92	2,9	0,31	1,67	3,9	0,29	1,49	4,3
0,6	0,29	1,89	5,7	0,22	1,46	5,7	0,17	1,20	5,1	0,16	1,04	4,6
0,7	0,14	1,20	7,3	0,10	0,87	5,6	0,08	0,71	4,4	0,08	0,62	3,7
0,8	0,05	0,56	5,1	0,04	0,42	3,7	0,03	0,35	2,8	0,03	0,32	2,3
0,9	0,01	0,19	2,1	0,01	0,15	1,5	0,01	0,13	1,2	0,01	0,12	1,1
1,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0

Таблица 18

Значения функций S(z), S¢(z) и S²(z) для Кузбасса

z	N = 1	N = 0,9	N = 0,8	N ≤ 0,7
	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)
	1,00	0,0	0,0	1,00	0,0	-4,5	1,00	0,0	-6,4	1,00	0,0	-8,3
0,1	0,99	0,2	-2,3	0,97	0,6	-5,5	0,96	0,7	-6,8	0,96	0,8	-8,0
0,2	0,95	0,5	-5,6	0,89	1,1	-6,5	0,85	1,4	-6,2	0,83	1,6	-5,9
0,3	0,86	1,6	-10,8	0,74	1,7	-6,0	0,68	1,8	-3,5	0,65	1,9	-1,0
0,4	0,66	2,6	-8,0	0,55	2,2	-2,5	0,49	2,0	-0,4	0,46	1,8	3,4
0,5	0,38	2,3	6,8	0,32	2,0	8,0	0,31	1,7	6,0	0,29	1,4	4,0
0,6	0,17	1,5	11,0	0,16	1,2	6,5	0,16	1,1	5,1	0,16	1,0	3,6
0,7	0,08	0,6	6,0	0,08	0,7	4,5	0,08	0,7	3,7	0,08	0,7	2,9
0,8	0,03	0,3	2,0	0,03	0,3	2,5	0,03	0,3	2,2	0,03	0,3	2,0
0,9	0,01	0,1	1,0	0,01	0,2	1,0	0,01	0,2	1,1	0,01	0,2	1,2
1,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0

Таблица 19

Значения функций S(z), S¢(z) и S²(z) для Челябинского бассейна

z	N = 1	N = 0,9	N = 0,8	N ≤ 0,7
	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)
	1,00	0,0	0,0	1,00	0,0	-6,0	1,00	0,0	-9,0	1,00	0,0	-9,0
0,1	0,95	0,9	-8,0	0,93	1,1	-8,8	0,91	1,2	-8,5	0,92	1,0	-8,5
0,2	0,83	1,6	-6,0	0,78	1,7	-4,5	0,76	1,7	-3,8	0,80	1,8	-6,0
0,3	0,65	2,1	-1,5	0,58	2,0	0,3	0,57	1,9	0,3	0,57	2,2	0,5
0,4	0,42	1,9	4,0	0,38	1,7	4,0	0,37	1,7	4,0	0,37	1,7	5,0
0,5	0,28	1,2	5,0	0,24	1,2	4,5	0,24	1,1	4,3	0,22	1,2	4,5
0,6	0,18	0,9	3,5	0,14	0,8	3,5	0,14	0,8	3,3	0,13	0,8	3,5
0,7	0,10	0,6	2,8	0,08	0,5	2,5	0,08	0,5	2,5	0,07	0,5	2,5
0,8	0,05	0,4	2,0	0,04	0,3	1,8	0,04	0,3	1,8	0,04	0,3	1,5
0,9	0,02	0,2	1,2	0,02	0,2	0,8	0,02	0,2	0,8	0,02	0,2	0,9
1,0	0,0	0,0	0,0	0,00	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0

Таблица 20

Значения функций S(z), S¢(z) и S²(z) для Кизеловского бассейна

z	N = 1	N = 0,9	N = 0,8	N ≤ 0,7
	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)
	1,00	0,0	0,0	1,00	0,0	-5,5	1,00	0,0	-6,8	1,00	0,0	-7,0
0,1	0,97	0,6	-5,3	0,96	0,7	-5,8	0,95	0,7	-6,0	0,93	0,8	-6,0
0,2	0,89	1,1	-5,0	0,87	1,2	-4,8	0,86	1,2	-4,5	0,84	1,2	-4,0
0,3	0,76	1,6	-3,8	0,73	1,6	-3,5	0,71	1,6	-3,0	0,69	1,6	-2,5
0,4	0,58	1,8	-0,8	0,56	1,8	-0,8	0,54	1,8	-0,5	0,52	1,7	1,0
0,5	0,40	1,7	2,0	0,37	1,7	2,5	0,35	1,7	2,8	0,35	2,0	3,5
0,6	0,24	1,4	3,8	0,22	1,3	4,3	0,20	1,3	4,5	0,22	1,6	6,0
0,7	0,12	1,0	4,3	0,11	0,9	4,0	0,10	0,8	4,0	0,12	0,8	5,5
0,8	0,05	0,6	3,5	0,05	0,5	3,3	0,04	0,5	3,0	0,07	0,5	2,5
0,9	0,01	0,3	1,8	0,01	0,3	1,8	0,01	0,2	1,5	0,03	0,3	1,5
1,0	0,0	0,0	0,0	0,00	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0

Таблица 21

Значения функций S(z), S¢(z) и S²(z) для месторождений Печорского бассейна и Интинского месторождения

z	N = 1	N = 0,9	N ≤ 0,8
	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)
	1,00	0,0	0,0	1,00	0,0	-3,25	1,00	0,0	-5,25
0,1	0,99	0,30	-4,00	0,98	0,40	-4,50	0,96	0,55	-5,00
0,2	0,94	0,80	-6,50	0,91	0,90	-5,75	0,89	1,00	-4,75
0,3	0,83	1,60	-6,75	0,79	1,55	-5,50	0,76	1,50	-3,75
0,4	0,62	2,15	-1,75	0,61	2,00	-1,75	0,59	1,85	-1,50
0,5	0,40	1,95	3,75	0,40	1,90	3,00	0,39	1,80	2,50
0,6	0,23	1,40	5,25	0,23	1,40	5,00	0,23	1,35	4,50
0,7	0,12	0,90	4,25	0,12	0,90	4,25	0,12	0,90	4,00
0,8	0,05	0,55	3,00	0,05	0,55	3,00	0,05	0,55	3,00
0,9	0,01	0,25	1,50	0,01	0,25	1,50	0,01	0,25	1,50
1,0	0,0	0,0	0,0	0,00	0,0	0,0	0,0	0,0	0,0

Таблица 22

Значения функций S(z), S¢(z) и S²(z) для Буланашского месторождения

z	N = 1	N = 0,8	N ≤ 0,6
	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)	S(z)	S¢(z)	S²(z)
	1,00	0,0	0,0	1,00	0,0	-6,5	1,00	0,0	-9,5
0,1	0,98	0,5	-7,5	0,96	0,7	-8,0	0,94	1,1	-8,2
0,2	0,90	1,3	-5,0	0,84	1,6	-7,0	0,79	1,8	-5,2
0,3	0,73	2,1	-2,3	0,65	2,2	-3,2	0,58	2,2	-0,5
0,4	0,50	2,3	2,5	0,43	2,1	3,2	0,36	1,9	4,8
0,5	0,30	1,6	6,0	0,26	1,4	5,5	0,22	1,3	5,3
0,6	0,17	1,0	4,8	0,14	0,9	4,6	0,12	0,8	4,1
0,7	0,09	0,6	3,8	0,07	0,5	3,1	0,06	0,4	2,7
0,8	0,04	0,3	2,3	0,04	0,2	1,9	0,03	0,2	1,6
0,9	0,01	0.1	1,4	0,01	0,1	1,2	0,01	0,1	1,0
1,0	0,0	0,0	0,0	0,00	0,0	0,0	0,0	0,0	0,0

Таблица 23

Значения функций S(z), S¢(z) и S²(z) для Подмосковного бассейна

z	S(z)	S¢(z)	S²(z)
	1,00	0,0	0,0
0,1	0,98	0,53	-6,5
0,2	0,88	1,60	-13,1
0,3	0,66	2,76	-6,4
0,35	-	2,85	-
0,4	0,38	2,65	7,1
0,5	0,16	1,57	10,1
0,6	0,05	0,70	7,5
0,7	0,01	0,20	2,9
0,8	0,005	0,04	0,6
0,9	0,002	0,02	0,1
1,0	0,0	0,0	0,0

в) в полумульде по восстанию

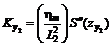, (39)

где S²(z) - функция типовой кривой кривизны, определяемая по таблицам 17-23 для соответствующих бассейнов (месторождений), в зависимости от коэффициентов N₁ - для точек главного сечения вкрест простирания пласта и N₂ - для точек главного сечения по простиранию пласта.

При неполной подработке (N₁,₂ < 1) кривизна в точке максимального оседания определяется по средней длине полумульды L_ср = 0,5(L₁ + L₂).

Горизонтальные сдвижения в точках главных сечений мульды:

а) по простиранию

x_х = 0,5a₀h_mS¢(z_x); (40)

б) в сторону обратную простиранию

x_х = -0,5a₀h_mS¢(z_x); (41)

в) в полумульде по падению

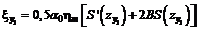; (42)

г) в полумульде по восстанию

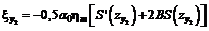. (43)

Значение В определяется по формуле:

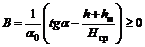, (44)

где a₀ - относительное максимальное горизонтальное сдвижение, определяемое по разделу 7;

a - угол падения пласта;

H_ср - средняя глубина разработки, м;

h - мощность наносов;

h_м - мощность горизонтально залегающих (a ≤ 5°) мезозойских отложений, м.

Значения функции S(z_х) определяются по таблицам 17-23 для соответствующих бассейнов (месторождений) в зависимости от коэффициента N₂, а значения функций 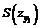; ; ; 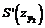определяются по таблицам 17-23 для соответствующих бассейнов (месторождений) в зависимости от коэффициента N₁.

Горизонтальные деформации в точках главных сечений мульды:

а) по простиранию

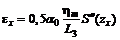; (45)

б) в полумульде по падению

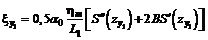; (46)

в) в полумульде по восстанию

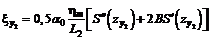. (47)

Значения функций S²(z_х) и S¢(z_х) определяются по таблицам 17-23 для соответствующих бассейнов (месторождений) в зависимости от коэффициента N₂; значения функций S²(z_у) и S¢(z_у) определяются по таблицам 17-23 для соответствующих бассейнов (месторождений) в зависимости от коэффициента N₁.

При неполной подработке (N₁ < 1) горизонтальные деформации в точке максимального оседания определяются по средней длине полумульды L_ср = 0,5(L₁ + L₂).

Промежуточные значения функций S(z), S¢(z) и S²(z), в таблицах 17-23, определяются интерполяцией.

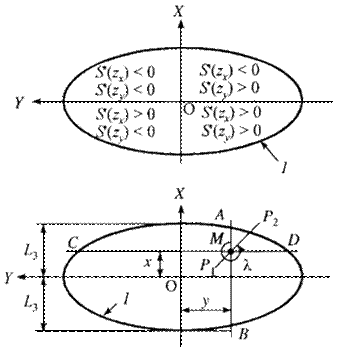
Рис. 9. Схема расположения координатных осей и знаки функций при расчете сдвижений и деформаций в заданной точке мульды:

1 - граница мульды сдвижения; АВ - сечение мульды сдвижения параллельное главному сечению по простиранию пласта; СD - то же, вкрест простирания пласта; Р₁Р₂ - сечение мульды в произвольном (заданном) направлении

4.2.2. Сдвижения и деформации в заданных точках мульды сдвижения (рис. 9) определяются следующим образом.

Оседание земной поверхности в точке М рассчитываем по формуле (см. рис. 9):

h_xy = h_mS(z_x)S(z_y), (48)

где S(z_x) - функция S(z), определяется по таблицам 17-23 в зависимости от координаты точки М; z_x = x/L₃;

S(z_y) - функция S(z), определяется по таблицам 17-23 в зависимости от координаты точки М, z = 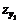= Y₁/L₁ (если точка М расположена в полумульде по падению) или координаты 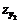= Y₂/L₂ (если точка М расположена в полумульде по восстанию);

x - абсцисса точки М - расстояние от оси Y (главного сечения мульды вкрест простирания пласта) до параллельного оси Y сечения СД (см. рис. 9), проходящего через точку М;

Y₁ (Y₂) - ордината точки М, расстояние от оси Х (главного сечения мульды по простиранию пласта) до параллельного ей сечения АВ, проходящего через точку М.

Оси координат располагаются в плане следующим образом. Началом координат служит точка пересечения главных сечений мульды сдвижения по простиранию и вкрест простирания пласта (см. рис. 9), проходящих при неполной подработке через точку максимального оседания, а при полной через начало плоского дна. Ось Х проходит в главном сечении мульды по простиранию и направлена по простиранию пласта; ось Y проходит в главном сечении мульды вкрест простирания и направлена в сторону восстания пласта.

Наклон в рассматриваемой точке М:

а) по направлению простирания пласта

i_xy = i_xS(z_y); (49)

б) по направлению вкрест простирания пласта

i_yx = i_yS(z_x); (50)

в) в заданном направлении P₁P₂

i_l = i_xycosl + i_yxsinl, (51)

где i_x и i_y - наклоны в главном сечении мульды сдвижения, определяемые по формулам (33)-(36);

l - угол, отсчитываемый против часовой стрелки от направления простирания пласта до заданного направления P₁P₂ (см. рис. 9).

Кривизна в рассматриваемой точке М:

а) по направлению простирания пласта

K_xy = K_xS(z_y); (52)

б) по направлению вкрест простирания пласта

K_yx = K_yS(z_x); (53)

в) в заданном направлении

K_l = K_xycos²l + K_yxsin²l + j_xysin²l, (54)

где K_x и K_y - кривизна в главных сечениях мульды сдвижения, определяемая по формулам (37)-(39);

j_xy – скручивание поверхности, определяемое по формулам:

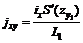- если точка М располагается в полумульде по падению пласта, или 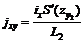, если точка М располагается в полумульде по восстанию пласта. Знаки S¢(z_y) определяется по рис. 9.

Горизонтальное сдвижение точки М:

а) по простиранию пласта

x_xy = x_xS(z_y); (55)

б) вкрест простирания

x_yx = x_yS(z_x), (56)

где x_x и x_y - горизонтальные сдвижения в главных сечениях мульды, определяемые по формулам (40)-(43);

в) в заданном направлении P₁P₂ (см. рис. 9)

x_l = x_xycosl + x_yxsinl. (57)

Горизонтальные деформации в точке М

а) по простиранию пласта

e_xy = e_xS(z_y); (58)

б) вкрест простирания пласта

e_yx = e_yS(z_x), (59)

где e_x и e_y - горизонтальные деформации в главных сечениях мульды, определяются по формулам (45)-(47);

в) в заданном направлении P₁P₂

e_l = e_xycos²l + e_yxsin²l + 0,5D_xysin²l, (60)

где D_xy - скашивание (сдвиг) земной поверхности, определяется по формулам:

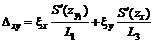, если точка М расположена в полумульде по падению, или 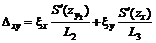, если точка М расположена в полумульде по восстанию пласта. Знаки S¢(z_x) и S¢(z_y) определяются по рис. 9.

Горизонтальные сдвижения в главных сечениях мульды x_x и x_y определяются из выражений (40)-(43).

4.2.3. Сосредоточенные деформации определяются следующим образом.

Сосредоточенные сдвиги в горизонтальной плоскости при a > 35° (при наличии данных наблюдений, подтверждающих их образование) на выходе контактов слоев на земную поверхность или под наносы мощностью до 10 м в точке с координатами х, y определяются по формуле:

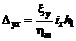, (61)

где x_y - горизонтальные сдвижения в главном сечении мульды сдвижения вкрест простирания пласта в точке (0; y) , определяемые по формулам (42)-(43);

i_x - наклоны в главном сечении мульды по простиранию в точке (х; 0), определяемые по формулам (33)-(34);

h₁ - мощность деформирующихся пачек, определяется по данным наблюдений; при отсутствии данных наблюдений принимается равной h₁ = 30 м.

При мощности наносов h > 10 м горизонтальные сдвиги определяются по заключению специализированной организации.

Радиус кривизны земной поверхности в местах сосредоточенных деформаций для различных бассейнов (месторождений) при a_п ≥ a > 45 определяют по табл. 24 в зависимости от ожидаемых наклонов поверхности.

Таблица 24

Радиусы кривизны в местах сосредоточенных деформаций

Бассейн	Наклоны, 1×10-3
До 1
Радиус кривизны Rc, км
Челябинский и другие с аналогичными свойствами пород	¥			4,5	4,0	2,0	1,5
Кузнецкий, Печорский, Кизеловский, Буланашское и другие с аналогичными свойствами пород	6,0	3,5	3,0	2,3	1,9	1,5	1,2

Обратные уступы в полумульде по падению (на месторождениях, где они установлены данными наблюдений) при a > 35° определяются по формуле (62):

h_y = l_y| 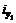|sin²(a - 15°)[1 + 2sin²(a - 15°)], (62)

где l_y - расстояние между уступами, определяемое по данным наблюдений; при отсутствии таких данных принимается l_y = 30 м;

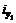- ожидаемые наклоны в полумульде по падению, определяемые по формуле (35).

4.2.4. Деформации от ранее пройденных (старых*) выработок рассчитываются при следующих условиях:

_____________

* Под ранее пройденной (старой) выработкой понимается выработка, пройденная до начала строительства охраняемых объектов.

а) ранее пройденная (старая) выработка находится в зоне влияния действующей (проектируемой) выработки, т.е. выработки, от которой производится расчет сдвижений и деформаций, для определения мер охраны объектов;

б) старая горная выработка не была ранее в зоне влияния другой старой выработки.

Зона влияния ранее пройденной (старой) выработки, в которой рассчитываются деформации, определяется следующим образом:

а) при коэффициенте подработанности поверхности старой выработкой n₁(n₂) > 0,8 - от точки максимального оседания (начала зоны полных сдвижений) до границы мульды (рис. 10, а, зона 1-1);

б) при коэффициенте подработанности поверхности старой выработкой n₁(n₂) < 0,8 - в пределах всей мульды сдвижения от старой выработки (рис. 10, б, зона 1-1).

Расчеты деформаций от старых выработок, пройденных в пласте, где проектируется проведение смежных выработок (см. рис. 10), выполняются следующим образом:

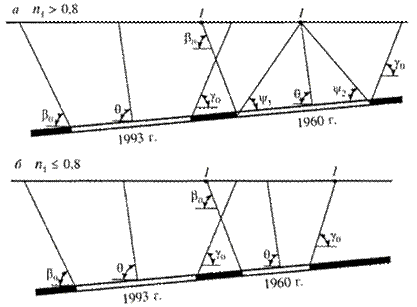
Рис. 10. Схема к расчету деформаций от ранее пройденных выработок:

а - при коэффициенте подработанности поверхности от ранее пройденной выработки

n₁ > 0,8; б - то же, n₁ < 0,8

при коэффициенте подработанности поверхности старой выработкой n₁(n₂) ≥ 0,6 деформации в зоне влияния старой выработки определяются по формуле:

Д_c = 0,2Д_д, (63)

где Д_с - максимальные ожидаемые горизонтальные деформации, кривизна и наклоны от старой выработки;

Д_д - соответственно максимальные горизонтальные деформации, кривизна и наклоны от действующей выработки; при коэффициенте подработанности n₁(n₂) < 0,6 расчет деформаций от старых выработок выполняется с привлечением специализированных организаций. Полученные деформации от смежных старых выработок суммируются с соответственными деформациями от действующих (проектируемых) выработок.

Расчет сдвижений и деформаций от старых выработок, пройденных в вышележащих (нижележащих) пластах выполняется путем увеличения максимального оседания и соответственно деформаций от действующих выработок, а также с учетом изменения граничных углов под влиянием старых выработок (разд. 7).

Учет влияния старых выработок в условиях крепких пород при наличии мощных слоев песчаников в массиве (антрацитовые районы) выполняется с привлечением специализированных организаций.

4.2.5. Расчет ожидаемых сдвижений и деформаций, вызванных сдвижением пород по напластованию, выполняется в условиях тех бассейнов и месторождений, где эти сдвижения и деформации установлены по результатам инструментальных наблюдений.

Сдвижения и деформации горного массива и земной поверхности, вызванные сдвижениями пород по напластованию, возникают в области, ограниченной на разрезе вкрест простирания вертикальной линией, отстоящей от выхода почвы разрабатываемого пласта под наносы на 10 м, и вертикальной линией, проведенной через верхнюю границу выработки (рис. 11, зона 1-1¢).

В тех случаях, когда глубина верхней границы выработки менее 30 м, за верхнюю границу зоны сдвижений пород по напластованию принимается точка пересечения вертикальной линии с поверхностью, проходящей через угольный пласт, залегающий на глубине 30 м.

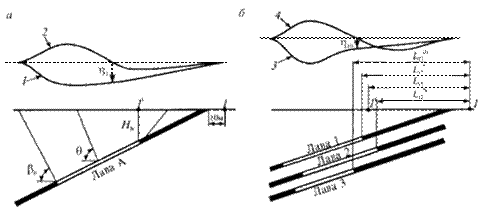
Рис. 11. Схема к расчету сдвижений и деформаций, вызванных сдвижением пород по напластованию:

а - при выемке одиночных пластов; б - при выемке свит пластов; 1 - оседания от лавы А;

2 - горизонтальные сдвижения от лавы А; 3 - оседания от лав 1+2+3; 4 - горизонтальные сдвижения от лав 1+2+3

Сдвижения горных пород по напластованию рассчитывают при следующих условиях:

45° > a > r¢;

(64)

h_н ≤ 0,2H_в,

где r¢ - угол трения по наиболее слабым контактам; при отсутствии полевых испытаний принимается r¢ = 13°;

h_н - мощность наносов;

H_в - глубина верхней границы выработки.

При углах падения a > 45° и h_н ≥ 0,2H_в расчеты сдвижений и деформаций по напластованию выполняются с привлечением специализированных организаций.

Оседание земной поверхности в точке 1¢ от влияния выработки на горизонте I, вызванное сдвижениями пород по напластованию,

h_н = h₁sin²a, (65)

где h₁ - оседание земной поверхности от выработок первого горизонта в точке, где горизонтальные сдвижения x = 0 (см. рис. 11) либо направлены в сторону падения пласта.

Оседание и горизонтальные сдвижения в мульде рассчитываются по рекомендациям п. 4.2.

Горизонтальные сдвижения в точке 1¢ от влияния выработки на горизонте 1.

x_н = h₁sinacosa. (66)

Оседание и горизонтальные сдвижения в точке 1

x_н = h_н = 0. (67)

При разработке одиночных пластов наклоны, горизонтальные деформации и уступы определяются по формулам:

а) наклоны

в точке 1¢ (см. рис. 11);

(68)

в точке 1 (см. рис. 11) i_н = 0,

где H_в - глубина верхней границы выработки;

б) горизонтальные деформации

в точке 1¢ ,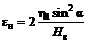

(69)

в точке 1 e_н = 0,

в промежуточных точках зоны 1-1¢ наклоны и горизонтальные деформации при отсутствии слабых контактов определяются линейной интерполяцией;

в) величины уступов на выходе разрабатываемого пласта, угольных пропластков и ранее вынутых пластов

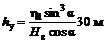. (70)

Величины горизонтальных деформаций на выходах угольных пропластков и ранее вынутых пластов рассчитываются по формуле (69) и умножаются на коэффициент k_п = 3,0.

Величины наклонов и горизонтальных деформаций, вызванных подвижками пород по напластованию при разработке свит пластов, в тех случаях, когда расстояния между проекциями верхних границ выработок на земную поверхность меньше половины глубины верхней границы выработки в верхнем пласте, определяются по формулам (см. рис. 11, б):

а) наклоны

в точке 1¢ ;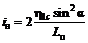

(71)

в точке 1 i_н = 0;

б) горизонтальные деформации

в точке 1¢ ;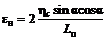

(72)

в точке 1 e_н = 0,

где 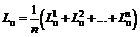; ; 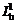; 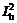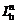- соответственно расстояния по горизонтали от точки 1 (см. рис. 11, б) до проекций верхних границ выработок на земную поверхность в пластах 1, 2, ..., n; положение точки 1 определяется по данным наблюдений, либо обосновывается по заключению специализированной организации;

h_1с - суммарное максимальное оседание поверхности от свиты пластов в точке, где горизонтальные сдвижения равны нулю, либо направлены по падению пласта (см. рис. 11, б).

В других случаях расчеты сдвижений и деформаций в зоне подвижек пород по контактам выполняются по заключению специализированной организации.