Аналитическое определение равнодействующей

Пучка сил

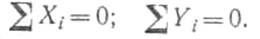
1. Алгебраический момент силы относительно точки. Плечо силы, моментная точка, правило знаков. Свойства моментов.

Случай сложения двух антипараллельных сил, равных по модулю. Такая система сил называется парой сил или просто парой (рис. 4.1).

Понятие пары сил введено в механику в начале XIX в. французским ученым Пуансо (1777—1859), который разработал теорию пар.

Плоскость, в которой расположена пара, называется плос­костью действия пары. Расстояние между линиями дей­ствия сил есть плечо пары. Эффект действия пары состоит в том, что она стремится вращать тело, к которому пара приложена. Ее вращательное действие определяется момен­том пары.

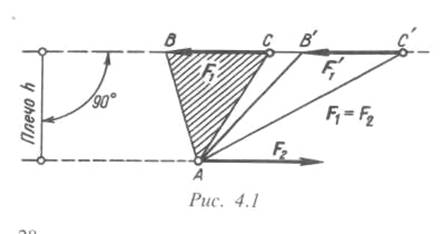
Моментом пары назы­вается произведение моду­ля одной из сил, состав­ляющих пару, на плечо:

M(F_l, F₂) = F₁h = F₂h = m.

Момент пары и мо­мент силы имеют один­аковую размерность.

Условимся считать момент пары положительным, если она стремится вращать свое плечо против часовой стрелки, и на­оборот.

Основные свойства пары

Основные свойства пары характеризуются следующими тремя теоремами.

Теорема I. Пара сил не имеет равнодействующей.

Это значит, что при F₁=F₂ равнодействующая не существует.

Из этой теоремы следует, что пара сил не может быть уравновешена одной силой; пара сил может быть уравновешена только парой.

Теорема II. Алгебраическая сумма моментов сил, составля­ющих пару, относительно любой точки плоскости действия пары есть величина постоянная, равная моменту пары.

Из этой теоремы следует, что при любом центре моментов пара сил войдет в уравнение моментов с одним и тем же знаком и одной и той же величиной.

Теорема III. Алгебраическая сумма проекций сил пары на ось всегда равна нулю.

Из этой теоремы следует, что пара сил не входит ни в уравнение сил, ни в уравнение проекций сил.

1. Пара сил. Плоскость пары, плечо пары. Алгебраический момент пары сил.

Две антипараллельные силы, равные по модулю. Такая система сил называется парой сил или просто парой (рис. 4.1).

Плоскость, в которой расположена пара, называется плос­костью действия пары. Расстояние между линиями дей­ствия сил есть плечо пары. Эффект действия пары состоит в том, что она стремится вращать тело, к которому пара приложена. Ее вращательное действие определяется момен­том пары.

1. Свойства момента пары сил.

Основные свойства пары

Основные свойства пары характеризуются следующими тремя теоремами.

Теорема I. Пара сил не имеет равнодействующей.

Это значит, что при F₁=F₂ равнодействующая не существует.

Из этой теоремы следует, что пара сил не может быть уравновешена одной силой; пара сил может быть уравновешена только парой.

Теорема II. Алгебраическая сумма моментов сил, составля­ющих пару, относительно любой точки плоскости действия пары есть величина постоянная, равная моменту пары.

Из этой теоремы следует, что при любом центре моментов пара сил войдет в уравнение моментов с одним и тем же знаком и одной и той же величиной.

Теорема III. Алгебраическая сумма проекций сил пары на ось всегда равна нулю.

Из этой теоремы следует, что пара сил не входит ни в уравнение сил, ни в уравнение проекций сил.

1. Векторный момент силы относительно точки. Свойства момента. Векторный момент пары сил, свойства момента.

Теорема о сложении пар

Теорема. Всякая плоская система пар эквивалента одной результирующей паре, момент которой равен алгебраической сумме моментов данных пар.

1. Эквивалентные пары сил. Векторный момент пары сил. Условие равновесия пар сил.

Эквивалентные пары

Две пары называются эквивалентными, если одну из них можно заменить другой, не нарушая механического состояния свободного твердого тела.

Теорема об эквивалентных парах формулируется так: если моменты двух пар алгебраически равны, то эти пары эквивалентны.

Из доказанной теоремы об эквивалентных парах вытекает четыре следствия:

1. не изменяя механического состояния тела, пару можно
перемещать как угодно в плоскости ее действия;

2. не изменяя механического состояния тела, можно менять
силы и плечо пары, но так, чтобы ее момент остаются неизменным;

3. чтобы задать пару, достаточно задать ее момент, поэтому иногда слово «пара» заменяют словом «момент» и условно изображают его так, как показано на рис. 4.6;

4. условия равновесия плоской системы па­раллельных сил будут справедливы, если вместе с такой системой действуют и пары сил, так как их можно повернуть в плоскости действия и поставить силы пары параллельно другим силам системы.