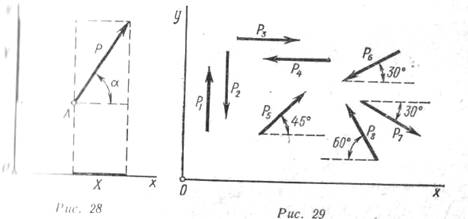
Определение равнодействующей двух сил, приложенных к точке
Простейшую плоскую систему сходящихся сил образуют две силы, приложенные к точке (их линии действия обязательно лежат в одной плоскости).
Равнодействующая двух сил, приложенных к точке, может быть найдена непосредственно по аксиоме статики) построением параллелограмма сил. При этом угол между линиями действия сил необходимо как можно точнее отложить по транспортиру, а векторы сил построить, строго соблюдая выбранный масштаб.
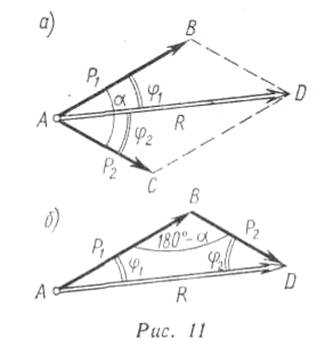
Разложение силы на две сходящиеся
Составляющие
Построением параллелограмма или треугольника сил может быть решена и обратная задача—разложение данной силы на две составляющие.
Для решения этой задачи необходимо, кроме данной силы, знать еще каких-нибудь два условия, достаточных для построения параллелограмма или треугольника сил, а именно модули обеих составляющих сил или их направления, или величину и направления одной из них.
- Силовой многоугольник. Геометрическое условие равновесия системы сходящихся сил.
Многоугольник сил
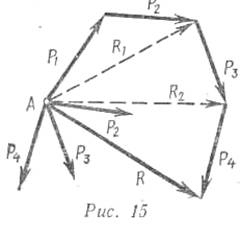
Если в точке А сходятся не две, а несколько сил, то равнодействующая их определяется по правили силового многоугольника. Из конца первой силы откладывают по величине и направлению вторую, из конца второй—по величине и направлению третью и т. д. Вектор, соединяющий начало первой силы и конец последней, т.е. замыкающий Силовой многоугольник и направленный навстречу составляющим силам, определяет по величине и направлению равно действующую данных сил (рис. 15). Величина и направление этой равнодействующей не зависят от порядка сложения сил.
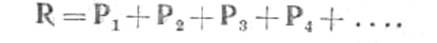 Следовательно, равнодействующая какого угодно числа сил, приложенных в одной точке, приложена в той же точке и равна геометрической сумме данных сил:
Следовательно, равнодействующая какого угодно числа сил, приложенных в одной точке, приложена в той же точке и равна геометрической сумме данных сил:
Таким образом, замыкающая сторона силового многоугольника вполне определяет равнодействующую пучка сил по величине, направлению и положению. Последнее равенство короче можно представить так:

где Σ обозначает знак суммы для сил Рi ( причем индекс i приобретает последовательно значения от 1 до n.
Сложение сходящихся сил по правилу многоугольника, как видно из рис. 15, есть результат последовательного сложения данных сил по правилу треугольника, а именно:
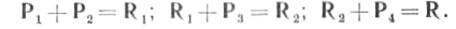
Силы системы взаимно уравновешиваются, если равнодействующая их (замыкающая сторона многоугольника) равна нулю (R = 0), т.е. если силовой многоугольник замкнут.
Так как силовой многоугольник определяет равнодействующую вполне, то его замыкаемость и есть единственное (необходимое и достаточное) графическое условие равновесия пучка сил.
Случай трех сил
Особый интерес для техника-строителя представляет так называемый случай трех сил.
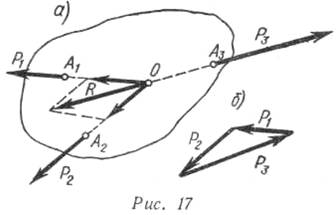
Если на тело действуют три непараллельные силы, лежащие в одной плоскости, и они находятся в равновесии, то линии их действия должны проходить через одну точку и треугольник сил должен быть замкнут.
- Проекция силы на ось. Аналитическое условие равновесия плоской системы сходящихся сил.
Проекция силы на ось
Все вопросы сложения, разложения и равновесия сходящихся сил могут быть решены аналитически — путем проецирования рассматриваемых сил на координатные
оси. Из геометрии известно, что проекцией вектора на
ось называется произведение величины этого вектора на
косинус угла между направлением вектора и положительным направлением оси. Обозначив проекцию силы Р на
ось х буквой X, а на ось у—Y, получим (рис. 28):
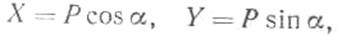
где φ- угол, образованный направлением силы Р с осью х.