Билет № 1: Этапы развития вычислительной техники

Билет № 1: Этапы развития вычислительной техники

Выделяют четыре этапа развития вычислительной техники:

§ Домеханический(ручной) — с 40—30-го тысячелетия до н. э.

§ Механический — с середины XVII в.

§ Электромеханический — с 90-х годов XIX в.

§ Электронный — со второй половины 40-х годов XX в.

§

Домеханический этап

Ручной период автоматизации вычислений начался на заре человеческой цивилизации и базировался на использовании частей тела, в первую очередь пальцев рук и ног. Пальцевый счет уходит корнями в глубокую древность, встречаясь в том или ином виде у всех народов и в наши дни. Конечно, счёт был примитивным, а уровень абстракции очень низким. Понятие числа максимально конкретно, оно неразрывно связано с предметом (т.е. это, например, не число «два», а «две рыбы», «два коня» и т.д.). Диапазон счёта невелик. Можно выделить три типа таких счётных приспособлений. Искусственные приспособления: зарубки (насечки) на различных предметах, в Южной Америке получают широкое распространение узелки на верёвках. Предметный счёт, когда используются предметы типа камешков, палочек, зёрен и т.д. Часто этот тип счёта использовался вместе с пальцевым. Счёт с помощью предметов был предшественником счёта на абаке - наиболее развитом счётном приборе древности, сохранившем некоторое значение в настоящее время (в виде русских счётов, китайского суань-паня и др.). Под абаком понимается счётный прибор, на котором отмечены места (колонки или строчки) для отдельных разрядов чисел.

Механический этап

Под механическим вычислительным устройством понимается устройство, построенное на механических элементах и обеспечивающее автоматическую передачу из низшего разряда в высший. Один из первых арифмометров, точнее «суммирующая машина», был изобретен Леонардо да Винчи (Leonardo da Vinci, 1452–1519) около 1500 года. Правда, о его идеях никто не знал на протяжении почти четырех столетий. Рисунок этого устройства был обнаружен только в 1967 году, и по нему фирма IBM воссоздала вполне работоспособную 13-разрядную суммирующую машину, в которой использован принцип 10-зубых колес.

Электромеханический этап

Электромеханический этап развития ВТ явился наименее продолжительным и охватывает всего около 60 лет — от первого табулятора Германа Холлерита (1887 г.) до первой ЭВМ ЕNIАС (1945 г.). Предпосылками создания проектов данного этапа явились как необходимость проведения массовых расчетов (экономика, статистика, управление и планирование и др.), так и развитие прикладной электротехники (электропривод и электромеханические реле), позволившие создавать электромеханические вычислительные устройства. Если вернуться к предыдущим этапам развития ВТ, то можно заметить, что каждый этап характеризуется созданием технических средств нового типа, обладающих более высокой производительностью и более широкой сферой применения, чем предыдущие этапы. Классическим типом средств электромеханического этапа был счетно-аналитический комплекс, предназначенный для обработки информации на перфокарточных носителях.

Электронный этап

В силу физико-технической природы релейная ВТ не позволяла существенно повысить скорость вычислений; для этого потребовался переход на электронные безынерционные элементы высокого быстродействия. К началу 40-х гг. 20 в. электроника уже располагала необходимым набором таких элементов. С изобретением М. Бонч-Бруевичем в 1913 г. триггера (электронное реле — двухламповый симметричный усилитель с положительной обратной связью; в качестве базовой компоненты использует электронную вакуумную лампу триод, изобретенную в 1906 г.) появилась реальная возможность создания быстродействующей электронной ВТ; электронные вычислительные машины (ЭВМ) ознаменовали собой новое направление в ВТ, интенсивно развиваемое и в настоящее время в различных направлениях. Первой ЭВМ (правда, специализированной, предназначенной для дешифровки) можно считать английскую машину Colossus, созданную в 1943 г. при участии Алана Тьюринга. Машина содержала около 2000 электронных ламп и обладала достаточно высоким быстродействием, однако была узкоспециализированной. Поэтому первой ЭВМ принято считать машину ЕNIАС (Еlесtrопic Numеriсаl Iпtеgrаtоr апd Сотрuter), созданную в США в конце 1945 г. Первоначально предназначенная для решения задач баллистики, машина оказалась универсальной, т.е. способной решать различные задачи.

Билет № 2: Основные понятия и категории информатики

Основные понятия информатики

Большинство ученых в наши дни отказываются от попыток дать строгое

определение информации и считают, что информацию следует рассматривать как

первичное, неопределимое понятие подобно множества в математике. Некоторые

авторы учебников предлагают следующие определения информации:

Информация – это знания или сведения о ком-либо или о чем-либо.

Информация – это сведения, которые можно собирать, хранить,

передавать, обрабатывать, использовать.

Информатика – наука об информации или

– это наука о структуре и свойствах информации,

– способах сбора, обработки и передачи информации или

– информатика, изучает технологию сбора, хранения и

переработки информации, а компьютер основной

инструмент в этой технологии.

Информация - от латинского information - сведения, разъяснения,

изложение.

В быту под информацией понимают сведения об окружающем мире и

протекающих в нем процессах.

В теории информации под информацией понимают не любые сведения, а лишь

те, которые снимают полностью или уменьшают существующую до их получения

неопределенность. По определению К.Шеннона, информация - это снятая

неопределенность.

Информация - это отражение внешнего мира с помощью знаков или

сигналов.

Информационная ценность сообщения заключается в новых сведениях,

которые в нем содержатся ( в уменьшении незнания).

Свойства информации 1)полнота, 2)достоверность, 3)ценность,

4)актуальность, 5)ясность.

Информация всегда связана с материальным носителем. Носителем

информации может быть:

. любой материальный предмет (бумага, камень и т.д.);

. волны различной природы: акустическая (звук), электромагнитная (свет,

радиоволна) и т.д.;

. вещество в различном состоянии: концентрация молекул в жидком растворе,

температура и т.д.

Машинные носители информации: перфоленты, перфокарты, магнитные ленты,

и т.д.

Сигнал - способ передачи информации. Это физический процесс, имеющий

информационное значение. Он может быть непрерывным или дискретным.

Сигнал называется дискретным, если он может принимать лишь конечное

число значений в конечном числе моментов времени.

Аналоговый сигнал - сигнал, непрерывно изменяющийся по амплитуде и во

времени.

Сигналы, несущие текстовую, символическую информацию, дискретны.

Аналоговые сигналы используют в телефонной связи, радиовещании,

телевидении.

Билет №9 Алгоритм перевода правильной дроби методом деления. Пример

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

.116 • 2 = 0.232

.232 • 2 = 0.464

.464 • 2 = 0.928

.928 • 2 = 1.856

.856 • 2 = 1.712

.712 • 2 = 1.424

.424 • 2 = 0.848

.848 • 2 = 1.696

.696 • 2 = 1.392

.392 • 2 = 0.784

и т. д.

Получим: 206,11610=11001110,00011101102

Естественная форма

В форме с фиксированной запятой в разрядной сетке выделяется строго определенное число разрядов для целой и для дробной частей числа. Левый (старший) разряд хранит признак знака (0 – "+", 1 – "-") и для записи числа не используется.

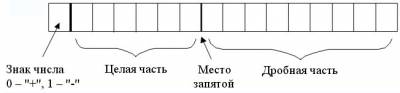
Сама запятая никак не изображается, но ее место строго фиксировано и учитывается при выполнении всех операций с числами. Независимо от положения запятой в машину можно вводить любые числа, т.к.

A = [A] · K^А,

где А – произвольное число, [A] – машинное изображение числа в разрядной сетке, K^А - масштабный коэффициент.

Естественная форма числа в неявном, условном виде реализуется формулой:

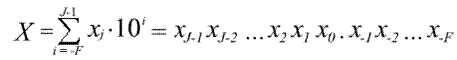
т.е. число записывается только с помощью набора значащих цифр x_j без явного указания их весов и знаков сложения между ними. Отсчет ведется от точки, которая обычно фиксируется между целой и дробной частями числа.

С фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной(например, 32,54; 0,0036; –108,2). Форма представления чисел с фиксированной запятой упрощает аппаратную реализацию ЭВМ, уменьшает время выполнения машинных операций, однако при решении задач на машине необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты находились в допустимом диапазоне представления. Если этого не соблюдать, то возможно переполнение разрядной сетки, и результат вычислений будет неверным. От этих недостатков в значительной степени свободны ЭВМ, использующие форму представления чисел с плавающей точкой, или нормальную форму. В современных компьютерах форма представления чисел с фиксированной запятой используется только для целых чисел.

С плавающей запятой (ПЛЗ) числа изображаются в виде:

X = ± M×P ^±r,

где M - мантисса числа (правильная дробь в пределах 0,1 ≤ M < 1), r - порядок числа (целое), P - основание системы счисления. Например, приведенные выше числа с фиксированной запятой можно преобразовать в числа с плавающей запятой так: 0,3254×10², 0,36×10^-2, –0,1082×10³.

Нормализованная экспоненциальная запись числа - это запись вида a= m*P^q, где q - целое число (положительное, отрицательное или ноль), а m - P-ичная дробь, у которой целая часть состоит из одной цифры. При этом m - мантиссa числа, q - порядк числа.

Tо есть нормальная форма реализуется формулой: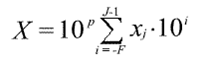

Нормальная форма представления имеет огромный диапазон чисел и является основной в современных ЭВМ.

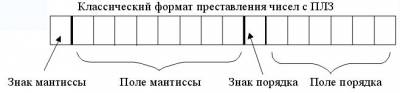
При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, используется так называемый смещённый порядок, который рассчитывается по формуле 2^(a-1) + ИП, где a - количество разрядов, отводимых под порядок, ИП - истинный порядок.

В конкретной ЭВМ диапазон представления чисел с плавающей запятой зависит от основания системы и числа разрядов для представления порядка. При этом у одинаковых по длине форматов чисел с плавающей запятой с увеличением основания системы счисления существенно расширяется диапазон представляемых чисел. Точность вычислений при использовании формата с плавающей запятой определяется числом разрядов мантиссы. Она увеличивается с увеличением числа разрядов.

Алгоритм представления числа с плавающей запятой:

1. перевести число из p-ичной системы счисления в двоичную;

2. представить двоичное число в нормализованной экспоненциальной форме;

3. рассчитать смещённый порядок числа;

4. разместить знак, порядок и мантиссу в соответствующие разряды сетки.

При представлении информации в виде десятичных многоразрядных чисел каждая десятичная цифра заменяется двоично-десятичным кодом. Для ускорения обмена информацией, экономии памяти и удобства операций над десятичными числами предусматриваются специальные форматы их представления: зонный (распакованный) и упакованный. Зонный формат используется в операциях ввода-операций. Для этого в ЭВМ имеются специальные команды упаковки и распаковки десятичных чисел.

Билет № 16: не знаю.

Билет № 17: не знаю.

Билет № 18: не знаю.

Билет № 19: Основные понятия алгебры логики. Законы и аксиомы

Законы алгебры логики

Законы алгебры логики базируются на аксиомах и позволяют преобразовывать логические функции. Логические функции преобразуются с целью их упрощения, а это ведет к упрощению цифровой схемы.

АКСИОМЫ алгебры логики описывают действие логических функций "И" и "ИЛИ" и записываются следующими выражениями:

0 * 0 = 0 0 * 1 = 0 1 * 0 = 0 1 * 1 = 1

0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 1

Всего имеется пять законов алгебры логики:

Закон одинарных элементов

1 * X = X
0 * X = 0
1 + X = 1
0 + X = X

Этот закон непосредственно следует из приведённых выше выражений аксиом алгебры логики.

Верхние два выражения могут быть полезны при построении коммутаторов, ведь подавая на один из входов элемента “2И” логический ноль или единицу можно либо пропускать сигнал на выход, либо формировать на выходе нулевой потенциал.

Второй вариант использования этих выражений заключается в возможности избирательного обнуления определённых разрядов многоразрядного числа. При поразрядном применении операции "И" можно либо оставлять прежнее значение разряда, либо обнулять его, подавая на соответствующие разряды единичный или нулевой потенциал. Например, требуется обнулить 6, 3 и 1 разряды. Тогда:

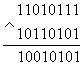
В приведённом примере отчётливо видно, что для обнуления необходимых разрядов в маске (нижнее число) на месте соответствующих разрядов записаны нули, в остальных разрядах записаны единицы. В исходном числе (верхнее число) на месте 6 и 1 разрядов находятся единицы. После выполнения операции "И" на этих местах появляются нули. На месте третьего разряда в исходном числе находится ноль. В результирующем числе на этом месте тоже присутствует ноль. Остальные разряды, как и требовалось по условию задачи, не изменены.

Точно так же можно записывать единицы в нужные нам разряды. В этом случае необходимо воспользоваться нижними двумя выражениями закона одинарных элементов. При поразрядном применении операции "ИЛИ" можно либо оставлять прежнее значение разряда, либо обнулять его, подавая на соответствующие разряды нулевой или единичный потенциал. Пусть требуется записать единицы в 7 и 6 биты числа. Тогда:

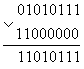
Здесь в маску (нижнее число) мы записали единицы в седьмой и шестой биты. Остальные биты содержат нули, и, следовательно, не могут изменить первоначальное состояние исходного числа, что мы и видим в результирующем числе под чертой.

Первое и последнее выражения позволяют использовать логические элементы с большим количеством входов в качестве элементов с меньшим количеством входов. Для этого неиспользуемые входы в схеме "И" должны быть подключены к источнику питания, как это показано на рисунке 1:

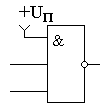
Рисунок 1. Схема "2И-НЕ", реализованная на элементе "3И-НЕ"

а неиспользуемые входы в схеме "ИЛИ" должны быть подключены к общему проводу схемы, как это показано на рисунке 2.

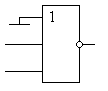
Рисунок 2. Схема "НЕ", реализованная на элементе "2И-НЕ"

Законы отрицания

a. Закон дополнительных элементов

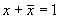
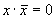
Выражения этого закона широко используется для минимизации логических схем. Если удаётся выделить из общего выражения логической функции такие подвыражения, то можно сократить необходимое количество входов элементов цифровой схемы, а иногда и вообще свести всё выражение к логической константе.

b. Двойное отрицание

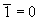
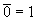
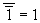
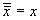
c. Закон отрицательной логики

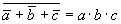
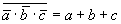
Закон отрицательной логики справедлив для любого числа переменных. Этот закон позволяет реализовывать логическую функцию "И" при помощи логических элементов "ИЛИ" и наоборот: реализовывать логическую функцию "ИЛИ" при помощи логических элементов "И". Это особенно полезно в ТТЛ схемотехнике, так как там легко реализовать логические элементы "И", но при этом достаточно сложно логические элементы "ИЛИ". Благодаря закону отрицательной логики можно реализовывать элементы "ИЛИ" на логических элементах "И". На рисунке 3 показана реализация логического элемента "2ИЛИ" на элементе "2И-НЕ" и двух инверторах.

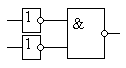
Рисунок 3. Логический элемент "2ИЛИ", реализованный на элементе "2И-НЕ" и двух инверторах

То же самое можно сказать и о схеме монтажного "ИЛИ". В случае необходимости его можно превратить в монтажное "И", применив инверторы на входе и выходе этой схемы.

Комбинационные законы

Комбинационные законы алгебры логики во многом соответствуют комбинационным законам обычной алгебры, но есть и отличия.

a. закон тавтологии (многократное повторение)

X + X + X + X = X
X * X * X * X = X

Этот закон позволяет использовать логические элементы с большим количеством входов в качестве элементов с меньшим количеством входов. Например, можно реализовать двухвходовую схему "2И" на элементе "3И", как это показано на рисунке 4:

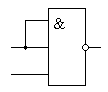
Рисунок 4. Схема "2И-НЕ", реализованная на элементе "3И-НЕ"

или использовать схему "2И-НЕ" в качестве обычного инвертора, как это показано на рисунке 5:

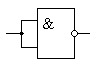
Рисунок 5. Схема "НЕ", реализованная на элементе "2И-НЕ"

Однако следует предупредить, что объединение нескольких входов увеличивает входные токи логического элемента и его ёмкость, что увеличивает ток потребления предыдущих элементов и отрицательно сказывается на быстродействии цифровой схемы в целом.

Для уменьшения числа входов в логическом элементе лучше воспользоваться законом одинарных элементов, как это было показано выше.

b. закон переместительности

A + B + C + D = A + C + B + D

c. закон сочетательности

A + B + C + D = A + (B + C) + D = A + B + (C + D)

d. закон распределительности

X1(X2 + X3) = X1X2 + X1X3 X1 + X2X3 = (X1 + X2)(X1 + X3) = /докажем это путём раскрытия скобок/ =
= X1X1 + X1X3 + X1X2 + X2X3 = X1(1 + X3 + X2) + X2X3 = X1 + X2X3

Определение

Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B, , , 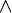, 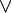0, 1}, где B — непустое множество, над элементами которого определены три операции:

отрицание (унарная операция),

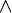конъюнкция (бинарная),

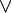дизъюнкция (бинарная),

а также константы — логический ноль 0 и логическая единица 1.

Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например 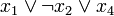). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например ).

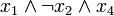Аксиомы

1.

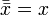
2.

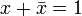
3.

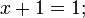
4.

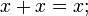
5.

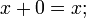
6.

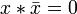
7.

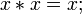
8.

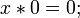
9.

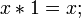
Понятие архитектуры ЭВМ.

Под архитектурой ЭВМ принято понимать совокупность общих принципов организации аппаратно-программных средств и их основных характеристик, определяющая функциональные возможности ЭВМ при решении соответствующих типов задач.

Архитектура ЭВМ охватывает обширный круг проблем, связанных с созданием комплекса аппаратных и программных средств и учитывающих большое количество определяющих факторов. Среди этих факторов самыми главными являются: стоимость, сфера применения, функциональные возможности, удобство в эксплуатации, а одним из основных компонентов архитектуры считаются аппаратные средства.

Архитектуру вычислительного средства необходимо отличать от его структуры. Структура вычислительного средства определяет его текущий состав на определенном уровне детализации и описывает связи внутри средства. Архитектура же определяет основные правила взаимодействия составных элементов вычислительного средства, описание которых выполняется в той мере, в какой необходимо для формирования правил их взаимодействия. Она устанавливает не все связи, а наиболее необходимые, которые должны быть известны для более грамотного использования применяемого средства.

Так, пользователю ЭВМ не важно, на каких элементах выполнены электронные схемы, схемно или программно исполняются команды и т. д. Важно несколько другое: как те или иные структурные особенности ЭВМ связаны с возможностями, предоставляемыми пользователю, какие альтернативные решения реализованы при создании машины и по каким критериям принимались решения, как связаны между собой характеристики устройств, входящих в состав ЭВМ, и какое действие они оказывают на общие характеристики компьютера. Другими словами, архитектура ЭВМ действительно отражает круг проблем, которые относятся к общему проектированию и построению вычислительных машин и их программного обеспечения.

36.

Архитектура фон Неймана

Основная статья: Архитектура фон Неймана

Большинство современных процессоров для персональных компьютеров в общем основаны на той или иной версии циклического процесса последовательной обработки данных, изобретённого^{[источник не указан 184 дня]} Джоном фон Нейманом.

Дж. фон Нейман придумал^{[источник не указан 184 дня]} схему постройки компьютера в 1946 году. Отличительной особенностью архитектуры фон Неймана является то, что инструкции и данные хранятся в одной и той же памяти.

В различных архитектурах и для различных команд могут потребоваться дополнительные этапы. Например, для арифметических команд могут потребоваться дополнительные обращения к памяти, во время которых производится считывание операндов и запись результатов.

Этапы цикла выполнения:

1. Процессор выставляет число, хранящееся в регистре счётчика команд, на шину адреса и отдаёт памяти команду чтения.

2. Выставленное число является для памяти адресом; память, получив адрес и команду чтения, выставляет содержимое, хранящееся по этому адресу, на шину данных и сообщает о готовности.

3. Процессор получает число с шины данных, интерпретирует его как команду (машинную инструкцию) из своей системы команд и исполняет её.

4. Если последняя команда не является командой перехода, процессор увеличивает на единицу (в предположении, что длина каждой команды равна единице) число, хранящееся в счётчике команд; в результате там образуется адрес следующей команды.

Данный цикл выполняется неизменно, и именно он называется процессом (откуда и произошло название устройства).

Во время процесса процессор считывает последовательность команд, содержащихся в памяти, и исполняет их. Такая последовательность команд называется программой и представляет алгоритм работы процессора. Очерёдность считывания команд изменяется в случае, если процессор считывает команду перехода, — тогда адрес следующей команды может оказаться другим. Другим примером изменения процесса может служить случай получения команды остановка или переключение в режим обработкипрерывания

.

Команды центрального процессора являются самым нижним уровнем управления компьютером, поэтому выполнение каждой команды неизбежно и безусловно. Не производится никакой проверки на допустимость выполняемых действий, в частности, не проверяется возможная потеря ценных данных. Чтобы компьютер выполнял только допустимые действия, команды должны быть соответствующим образом организованы в виде необходимой программы.

Скорость перехода от одного этапа цикла к другому определяется тактовым генератором. Тактовый генератор вырабатывает импульсы, служащие ритмом для центрального процессора. Частота тактовых импульсов называется тактовой частотой.

Операционные сиситемы.

Операционная система компьютера представляет собой комплекс взаимосвязанных программ, который действует как интерфейс между приложениями и пользователями с одной стороны, и аппаратурой компьютера с другой стороны. В соответствии с этим определением ОС выполняет две группы функций:

§ предоставление пользователю или программисту вместо реальной аппаратуры компьютера расширенной виртуальной машины, с которой удобней работать и которую легче программировать;

§ повышение эффективности использования компьютера путем рационального управления его ресурсами в соответствии с некоторым критерием.

Операционная система не только предоставляет пользователям и программистам удобный интерфейс к аппаратным средствам компьютера, но и является механизмом, распределяющим ресурсы компьютера.

К числу основных ресурсов современных вычислительных систем могут быть отнесены такие ресурсы, как процессоры, основная память, таймеры, наборы данных, диски, накопители на магнитных лентах, принтеры, сетевые устройства и некоторые другие. Ресурсы распределяются между процессами

Прозрачность сети - означает невидимость особенностей внутренней архитектуры сети для пользователя: в оптимальном случае он должен обращаться к ресурсам сети как к локальным ресурсам своего собственного компьютера.

39.

Билет № 1: Этапы развития вычислительной техники

Выделяют четыре этапа развития вычислительной техники:

§ Домеханический(ручной) — с 40—30-го тысячелетия до н. э.

§ Механический — с середины XVII в.

§ Электромеханический — с 90-х годов XIX в.

§ Электронный — со второй половины 40-х годов XX в.

§

Домеханический этап

Ручной период автоматизации вычислений начался на заре человеческой цивилизации и базировался на использовании частей тела, в первую очередь пальцев рук и ног. Пальцевый счет уходит корнями в глубокую древность, встречаясь в том или ином виде у всех народов и в наши дни. Конечно, счёт был примитивным, а уровень абстракции очень низким. Понятие числа максимально конкретно, оно неразрывно связано с предметом (т.е. это, например, не число «два», а «две рыбы», «два коня» и т.д.). Диапазон счёта невелик. Можно выделить три типа таких счётных приспособлений. Искусственные приспособления: зарубки (насечки) на различных предметах, в Южной Америке получают широкое распространение узелки на верёвках. Предметный счёт, когда используются предметы типа камешков, палочек, зёрен и т.д. Часто этот тип счёта использовался вместе с пальцевым. Счёт с помощью предметов был предшественником счёта на абаке - наиболее развитом счётном приборе древности, сохранившем некоторое значение в настоящее время (в виде русских счётов, китайского суань-паня и др.). Под абаком понимается счётный прибор, на котором отмечены места (колонки или строчки) для отдельных разрядов чисел.

Механический этап

Под механическим вычислительным устройством понимается устройство, построенное на механических элементах и обеспечивающее автоматическую передачу из низшего разряда в высший. Один из первых арифмометров, точнее «суммирующая машина», был изобретен Леонардо да Винчи (Leonardo da Vinci, 1452–1519) около 1500 года. Правда, о его идеях никто не знал на протяжении почти четырех столетий. Рисунок этого устройства был обнаружен только в 1967 году, и по нему фирма IBM воссоздала вполне работоспособную 13-разрядную суммирующую машину, в которой использован принцип 10-зубых колес.

Электромеханический этап

Электромеханический этап развития ВТ явился наименее продолжительным и охватывает всего около 60 лет — от первого табулятора Германа Холлерита (1887 г.) до первой ЭВМ ЕNIАС (1945 г.). Предпосылками создания проектов данного этапа явились как необходимость проведения массовых расчетов (экономика, статистика, управление и планирование и др.), так и развитие прикладной электротехники (электропривод и электромеханические реле), позволившие создавать электромеханические вычислительные устройства. Если вернуться к предыдущим этапам развития ВТ, то можно заметить, что каждый этап характеризуется созданием технических средств нового типа, обладающих более высокой производительностью и более широкой сферой применения, чем предыдущие этапы. Классическим типом средств электромеханического этапа был счетно-аналитический комплекс, предназначенный для обработки информации на перфокарточных носителях.

Электронный этап

В силу физико-технической природы релейная ВТ не позволяла существенно повысить скорость вычислений; для этого потребовался переход на электронные безынерционные элементы высокого быстродействия. К началу 40-х гг. 20 в. электроника уже располагала необходимым набором таких элементов. С изобретением М. Бонч-Бруевичем в 1913 г. триггера (электронное реле — двухламповый симметричный усилитель с положительной обратной связью; в качестве базовой компоненты использует электронную вакуумную лампу триод, изобретенную в 1906 г.) появилась реальная возможность создания быстродействующей электронной ВТ; электронные вычислительные машины (ЭВМ) ознаменовали собой новое направление в ВТ, интенсивно развиваемое и в настоящее время в различных направлениях. Первой ЭВМ (правда, специализированной, предназначенной для дешифровки) можно считать английскую машину Colossus, созданную в 1943 г. при участии Алана Тьюринга. Машина содержала около 2000 электронных ламп и обладала достаточно высоким быстродействием, однако была узкоспециализированной. Поэтому первой ЭВМ принято считать машину ЕNIАС (Еlесtrопic Numеriсаl Iпtеgrаtоr апd Сотрuter), созданную в США в конце 1945 г. Первоначально предназначенная для решения задач баллистики, машина оказалась универсальной, т.е. способной решать различные задачи.

Билет № 2: Основные понятия и категории информатики

Основные понятия информатики

Большинство ученых в наши дни отказываются от попыток дать строгое

определение информации и считают, что информацию следует рассматривать как

первичное, неопределимое понятие подобно множества в математике. Некоторые

авторы учебников предлагают следующие определения информации:

Информация – это знания или сведения о ком-либо или о чем-либо.

Информация – это сведения, которые можно собирать, хранить,

передавать, обрабатывать, использовать.

Информатика – наука об информации или

– это наука о структуре и свойствах информации,

– способах сбора, обработки и передачи информации или

– информатика, изучает технологию сбора, хранения и

переработки информации, а компьютер основной

инструмент в этой технологии.

Информация - от латинского information - сведения, разъяснения,

изложение.

В быту под информацией понимают сведения об окружающем мире и

протекающих в нем процессах.

В теории информации под информацией понимают не любые сведения, а лишь

те, которые снимают полностью или уменьшают существующую до их получения

неопределенность. По определению К.Шеннона, информация - это снятая

неопределенность.

Информация - это отражение внешнего мира с помощью знаков или

сигналов.

Информационная ценность сообщения заключается в новых сведениях,

которые в нем содержатся ( в уменьшении незнания).

Свойства информации 1)полнота, 2)достоверность, 3)ценность,

4)актуальность, 5)ясность.

Информация всегда связана с материальным носителем. Носителем

информации может быть:

. любой материальный предмет (бумага, камень и т.д.);

. волны различной природы: акустическая (звук), электромагнитная (свет,

радиоволна) и т.д.;

. вещество в различном состоянии: концентрация молекул в жидком растворе,

температура и т.д.

Машинные носители информации: перфоленты, перфокарты, магнитные ленты,

и т.д.

Сигнал - способ передачи информации. Это физический процесс, имеющий

информационное значение. Он может быть непрерывным или дискретным.

Сигнал называется дискретным, если он может принимать лишь конечное

число значений в конечном числе моментов времени.

Аналоговый сигнал - сигнал, непрерывно изменяющийся по амплитуде и во

времени.

Сигналы, несущие текстовую, символическую информацию, дискретны.

Аналоговые сигналы используют в телефонной связи, радиовещании,

телевидении.