Ограниченных кривыми поверхностями

6.2.1. Тень цилиндрического тела

Проведем на конкретных задачах необходимые рассуждения.

З а д а ч а 1

Построить собственные и падающие тени прямого кругового цилиндра, стоящего на плоскости V (рис. 27).

Плоскость основания кругового цилиндра, параллельная плоскости V, освещена световым потоком. Из всего множества лучей можно выделить два подмножества, которые образуют плоскости P и Т (на чертеже показаны их следы), касательные к поверхности цилиндра.

Касание происходит по двум образующим, до которых освещена половина боковой поверхности, другая половина находится в собственной тени, следовательно, обе образующие входят в состав контура собственной тени цилиндра. На границе света и тени находится часть дуги освещенного основания, которая также входит в состав этого контура.

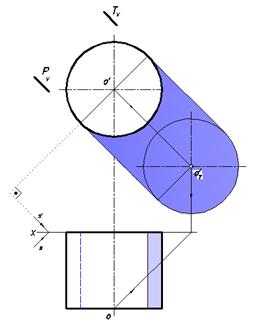
Рис. 27. Собственные и падающие тени цилиндрического тела

Освещенная боковая часть поверхности цилиндра и другое основание, расположенное в плоскости V и находящееся в собственной тени, образуют еще один участок замкнутого контура собственной тени цилиндра.

После этих рассуждений на горизонтальной проекции можно выделить цветом видимую часть контура собственной тени.

От этого контура определяется падающая тень. Вначале выполняется вспомогательное построение – определяется действительная тень точки O (o, o'), затем тень круга переднего основания цилиндра, равная этому кругу на основании свойства, приведенного ранее.

Две образующие, входящие в состав контура собственной тени цилиндра, стоящего на плоскости V, отбрасывают тени в виде отрезков прямых, касательных к данной и построенной окружностям. Общим контуром падающей тени будет полное очертание фигуры, изображенной на фронтальной проекции.

З а д а ч а 2

Построить собственные и падающие тени прямого кругового цилиндра, стоящего на плоскости H.

В предыдущей задаче подробно говорилось о построении контура собственной тени на цилиндрической поверхности. Проведя аналогичные рассуждения для цилиндра, стоящего на плоскости H, получим результат, показанный графически на рис. 28. Сплошной основной линией выделен контур собственной тени тела на ортогональных проекциях, а справа выполнено его наглядное изображение в изометрии.

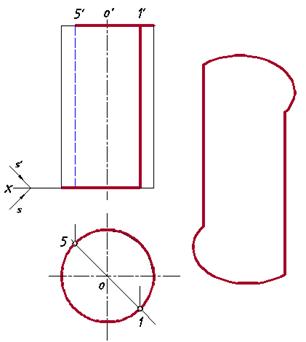
Рис. 28. Контур собственной тени на теле цилиндра

Построение падающей тени цилиндра начнем с определения действительной тени центра верхнего основания. Проведем через точку O(o, o') луч, параллельный направлению S (рис. 29). Поскольку аппликата точки О больше ее ординаты – действительная тень o_Т' окажется на плоскости V на основании вывода, приведенного ранее, а тень цилиндрического тела упадет одновременно на две плоскости проекций. Определим мнимую падающую тень окружности верхнего основания (точнее ее часть, входящую в контур собственной тени). Зная точку o_Т', найдем мнимую тень а_Т(ф).
С центром в этой точке проведем окружность радиуса основания цилиндра, на которой отметим мнимые тени 1_Т(ф), 2_Т(ф), …5_Т(ф) и по ним построим тени действительные.

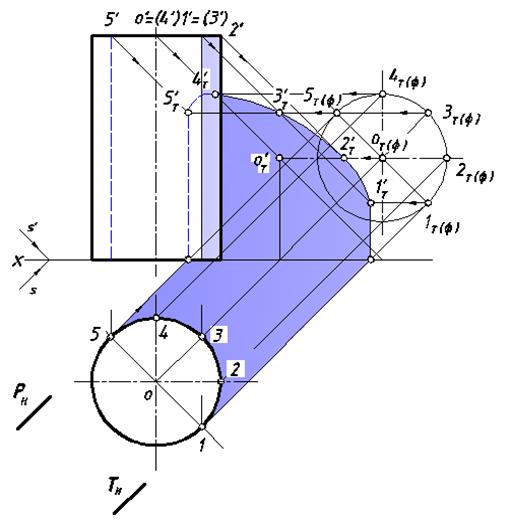
Рис. 29. Построение падающих теней объекта

с использованием мнимых

Покажем, как это сделать на примере точки (1, 1'). Через точку 1_Т(ф) проведем прямую, параллельную оси X, а через 1' – фронтальную проекцию луча, параллельную s'. На пересечении этих двух множеств определим действительную тень 1_Т'. Остальные действительные тени строятся аналогично.

В контур собственной тени входит часть окружности верхнего основания, действительная тень которого определяется пересечением лучевого эллиптического цилиндра с плоскостью V и образует фигуру сечения эллипс, содержащую точки 1_Т', 2_Т', … 5_Т'.

Две образующие цилиндра, лежащие в плоскостях P и Т, и полуокружность нижнего основания – оставшаяся часть контура собственной тени цилиндра, от этих геометрических образов построены падающие тени. Заметим, что точки 1_Т' и 5_Т' являются точками касания построенной дуги эллипса и падающими тенями двух образующих цилиндра.

З а д а ч а 3

Построить тени на цилиндрической оболочке (рис. 30).

При заданном направлении светового потока S часть наружной
и внутренней поверхности оболочки освещена, а границей освещенности будет левая очерковая образующая цилиндрической поверхности, проходящая через точку (4, 4'). На внутренней поверхности, на эпюре тень выделена бледным цветовым оттенком.

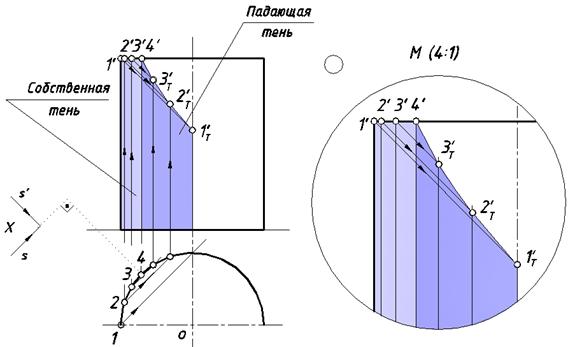
Рис. 30. Собственная и падающая тень цилиндрической оболочки

Часть дуги верхней дуги окружности от точки (1, 1') до (4, 4') находится на границе света и тени, следовательно, входит в состав контура собственной тени оболочки. Через каждую точку этой дуги проходит световой луч. Множество лучей образует поверхность эллиптического цилиндра. Ее пересечение с внутренней поверхностью оболочки – кривая четвертого порядка. Для построения этой кривой через вышеуказанные точки проводим световые лучи и отмечаем их пересечение с внутренней поверхностью. Полученные точки 1_Т', 2_Т', 3_Т' и 4_Т' соединяем плавной кривой – это падающая тень верхней дуги окружности. Лучевая горизонтально-проецирующая плоскость, проходящая через левую очерковую образующую, пересекает внутреннюю поверхность оболочки по прямой, ей параллельной, которая является ее падающей тенью.

З а д а ч а 4

Построить тень отрезка [AB] на поверхности цилиндрической оболочки (рис. 31).

Нахождение теней оболочки показано в предыдущей задаче, поэтому на чертеже, приведенном ниже, построения не показаны.

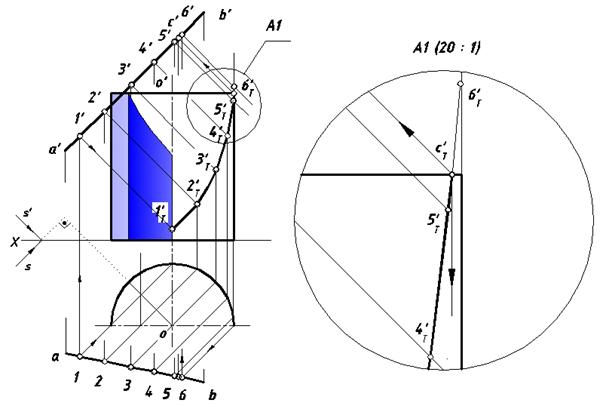
Рис. 31. Падающая тень отрезка [AB] на цилиндрическую оболочку

Для решения этой задачи использовано свойство проецирующей цилиндрической поверхности.

Множество лучей, проходящих через отрезок [AB], образует лучевую плоскость. Поскольку она является плоскостью общего положения
и пересекает все образующие цилиндрической оболочки, то результатом пересечения этих образов (тенью) будет эллипс (или часть его дуги).

Ввиду того, что эллипс это лекальная кривая, ее построение выполняется по множеству точек. Возьмем на отрезке [AB] точку (1, 1'). Это первая левая точка на данном отрезке, которая заведомо отбросит тень на внутреннюю поверхность оболочки.

Точки, расположенные на отрезке влево от нее, отбрасывают тени на наружную часть цилиндрической поверхности, которая на фронтальной проекции не видна ввиду своей непрозрачности, поэтому их тени строить не имеет смысла.

Проведем через точку (1, 1') луч, параллельный S и отметим его пересечение с цилиндрической поверхностью – действительную тень 1_Т'. Затем на отрезке [AB] возьмем случайные точки (2, 2'), (3, 3'), … (6, 6') и выполним аналогичные построения. Заметим, что точка 6_Т' оказалась за пределами левой очерковой образующей оболочки. Соединим построенные точки плавной кривой. Заметим, что точка С(с, c’), отбрасывающая тень на окружность верхнего основания цилиндра, может быть найдена лишь приближенно после построения эллиптической дуги по множеству случайных точек.

Для построения теней от одного объекта на другой инженеры-строители применяют следующие приемы:

метод секущих плоскостей;

метод обратного луча.

Архитекторы используют для своих целей девять различных способов (в данной работе они не приводятся).

Рассмотрим метод секущих плоскостей, который заключается
в следующем. Заданные геометрические объекты рассекаются вспомогательными плоскостями, параллельными световому лучу и перпендикулярными к какой-либо плоскости проекций. Затем определяются линии сечения каждого объекта вспомогательными плоскостями. Плоское сечение первого объекта необходимо для определения лучей, касательных к его поверхности. Пересечение этих лучей с поверхностью другого объекта позволяет найти точки контура тени, падающей с одного объекта на другой.

Решение задачи, приведенной выше, можно объяснить, применяя метод секущих плоскостей.

Проведем вспомогательные плоскости, параллельные световому лучу и перпендикулярные плоскости H (на чертеже следы этих плоскостей не обозначены). Каждая из этих плоскостей пересекает отрезок [AB] в точке, а цилиндрическую поверхность по образующей. Проведя через построенные точки, лучи до пересечения с оболочкой, найдем их действительные тени, по которым найдем очертание контура падающей тени отрезка [AB].

В приводимых ранее задачах использовался метод обратных лучей. Приведем общие рекомендации по применению этого метода.

Метод обратных лучей заключается в том, что вначале строятся контуры падающих теней от заданных геометрических объектов (эти построения для решения задачи являются вспомогательными). Далее определяются точки пересечения полученных контуров. Из этих точек проводятся в пространстве лучи, направление которых противоположно лучам света. Точки встречи проекций обратных лучей с соответствующими проекциями первого объекта позволяют определить те точки, которые отбрасывают тени на другой объект.

Покажем решение предыдущей задачи с применением метода обратных лучей.

Построим падающие тени двух геометрических объектов на плоскости проекций независимо друг от друга. При нахождении последних использованы мнимые тени. На падающей тени отрезка взяты случайные точки, которым обеспечена принадлежность оболочки цилиндра его образующими. С помощью обратных лучей на отрезке [AB] определены точки, которые отбросили тени на другой объект. Заметим, что применение этого способа позволяет точно построить точку С(с, c’).

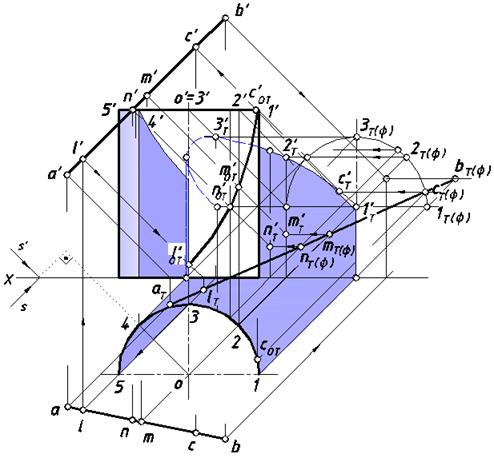
Рис. 32. Решение задачи с применением метода обратных лучей

На приведенных выше рисунках представлены решения задачи
с применением различных способов. В первом случае нельзя найти точное положение последней точки C(c, с’) отрезка [AB], которая отбросила тень на оболочку цилиндра, но можно обойтись без построений падающих теней. Применяя способ обратных лучей можно точно определить местонахождение точки C(c, с’),.но в этом случае, необходимо строить падающие тени.

6.2.2. Тень конического тела

З а д а ч а 1

Построить собственные и падающие тени конического тела на плоскости проекций H и V.

Обычно построение падающих теней начинается с определения контура собственных теней. Но в отдельных случаях выгоднее поступить наоборот.

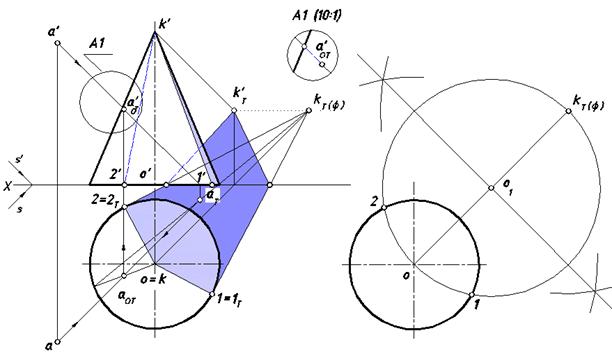
Рис. 33. Построение теней на поверхности конуса

Определим падающую тень вершины конуса – точку k_Т'. Из множества световых лучей, падающих на боковую поверхность конуса, можно выделить два подмножества, образующих лучевые плоскости общего положения, проходящие через вершину K(k, k’) и касающиеся окружности основания.

Если мысленно отбросить плоскость V, то падающая тень конического тела окажется на плоскости H. Поскольку на ней находится основание конуса, можно отметить, что 1 = 1_Т и 2 = 2_Т.

Проведя через точку k_Т(ф) касательные к окружности основания (их построение показано на рис. 33 справа), получим падающие тени двух образующих конуса, которые входят в состав контура собственной тени тела.

Рис. 34. Наглядное изображение контура собственной тени конуса

Полный контур собственной тени в наглядном виде представлен на рис. 34.

З а д а ч а 2

Определить тень точки А на поверхности конического тела.

Покажем различные варианты достижения желаемого результата
и воспользуемся графическим условием предыдущей задачи.

Применим метод обратных лучей, для реализации которого следует построить падающие тени двух объектов: точки A(a, a') и конуса на обе плоскости проекций. Через точку а_Т проведем падающую тень той образующей, которая содержит эту точку. Затем найдем горизонтальную проекцию этой образующей, на которой с помощью горизонтальной проекции обратного луча определим точку а_ОТ, а спомощью фронтальной – а_ОТ'.

Другой вариант решения задачи заключается в использовании известного алгоритма нахождения точки пересечения прямой с поверхностью:

1. через световой луч, содержащий точку A(a, a') и вершину K(k, k’) конуса, проведем плоскость общего положения (на рис. 35 она задана двумя пересекающимися прямыми);

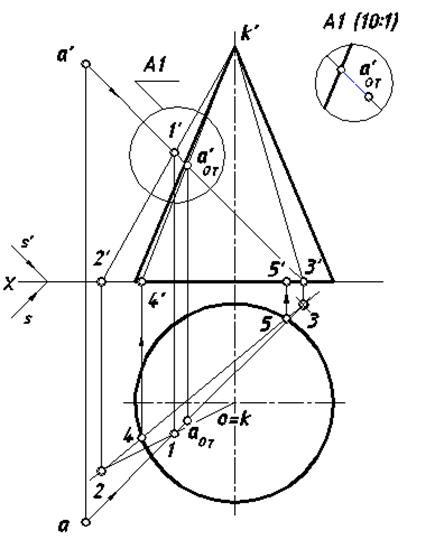
Рис. 35. Второй вариант решения задачи 6

2. определим линию пересечения проведенной плоскости с конической поверхностью (поскольку вспомогательная плоскость проходит через вершину конуса, результатом пересечения будут две образующие);

3. найдем точку пересечения светового луча с построенными образующими – искомую точку.

Заметим, что луч и две образующие пересекутся в двух точках, но только одна из них является действительной тенью точки A(a, a'), которая расположена перед главным меридианом конической поверхности (мнимая тень точки на эпюре не показана). Во избежание лишних построений найдены только фронтальные проекции образующих.

Возможный вариант решения задачи методом секущих плоскостей нецелесообразен, т.к. требует построения кривых второго порядка, что приведет лишь к приближенному решению поставленной задачи.

З а д а ч а 3

Построить тень отрезка [AB] на поверхности конуса методом секущих плоскостей.

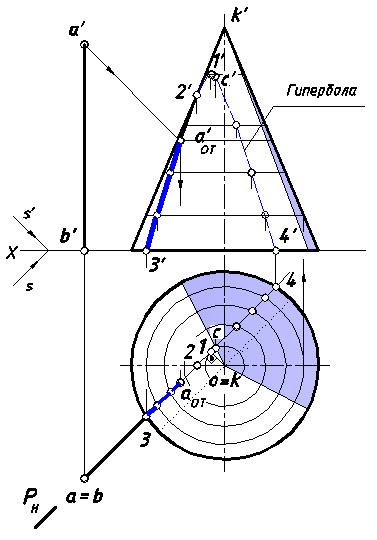
Рис. 36. Тень столба на поверхности конуса

Заключим отрезок [AB] в горизонтально-проецирующую плоскость P, параллельную направлению светового потока. Поскольку проведенная плоскость параллельна двум образующим конуса (на рис. 36 на горизонтальной проекции они показаны точечными линиями), она пересечет его по гиперболе.

Для ее построения поступим следующим образом. Ввиду того, что гипербола расположена в плоскости P, ее горизонтальная проекция на чертеже отображается отрезком [34]. Фронтальной проекцией гиперболы также будет гипербола (только с другими параметрами).

Любая лекальная кривая строится по множеству точек. Вначале определим характерные наинизшие точки (3, 3') и (4, 4'). Горизонтальную проекцию 1 наивысшей точки найдем на середине отрезка [34], а для построения ее фронтальной проекции 1' проведем параллель на конической поверхности, касательную к плоскости P. Еще одна характерная точка
(2, 2') расположена на главном меридиане, плоскость которого параллельна V. Между характерными точками намечаем случайные, горизонтальные проекции которых лежат на следе P_H. Этим точкам обеспечиваем принадлежность конической поверхности с помощью параллелей. Построив множество точек, соединяем их плавной кривой с учетом видимости непрозрачного тела. Часть гиперболы, заключенная между точками (3, 3')
и (а_ОТ, а_ОТ'), будет искомой тенью отрезка [AB] на поверхности конического тела.

6.2.3. Тень шара

Множество лучей, падающих на шар (рис. 37), образует световой цилиндр, соосный с его поверхностью, поэтому общим элементом для двух поверхностей (на основании леммы о пересечении соосных поверхностей) будет окружность, представляющая собой контур собственной тени шара. Теневой цилиндр пересекает плоскость H по эллипсу, который является падающей тенью шара. При нахождении очертаний этих теней можно использовать преобразование чертежа, например, метод перемены плоскостей проекций. Проведем плоскость V₁, параллельную направлению S,и построим новые фронтальные проекции шара и луча. Контур собственной тени шара отобразится на этой плоскости отрезком прямой [а₁' b₁']. Поскольку аппликаты всех точек контура в старой и новой системе плоскостей проекций одинаковы, можно найти множество точек, принадлежащих очертанию контура на обеих проекциях. Вначале определим с помощью характерных точек размеры осей эллипсов, в которые проецируется контур, а затем аналогичным образом построим необходимое количество случайных точек. Соединив плавной кривой линией одноименные проекции найденных точек с учетом видимости, получим проекции очертания контура собственной тени.

Построение падающей тени шара начнем с нахождения тени точки O(o, o’) (центра шара) – точки о_Т. Искомая тень на плоскости V₁ отобразится прямолинейным отрезком, равным большой оси искомого эллипса

Размер малой оси эллипса [m_1Т n_1Т] равен диаметру шара. Нахождение случайных точек очертания контура выполняется следующим образом:

На построенном контуре собственной тени берется произвольная точка
и определяется ее падающая тень. По множеству найденных падающих теней случайных точек завершаем построение эллипса (нахождение случайных точек на чертеже не показаны для удобства восприятия изображений).

Рис. 37. Построение теней на шаре

На рис. 38 показан другой способ нахождения теней шара. Как отмечалось выше, контурами собственных тенейшара являются эллипсы. Большие оси этих эллипсов – отрезки [ab] и [c'd'] равны диаметру шара. Точки A A(a, a’) и B (b, b’) расположены на экваторе сферы, а C(c, c’)
и D(d, d’) на главном меридиане, плоскость которого параллельна V. Учитывая симметрию эллипса относительно его большой и малой осей, можно получить точки, симметричные точкам c и d, и а' и b' на соответствующих проекциях. После этого по восьми полученным точкам выполнить очертание эллипсов с учетом видимости.

Построение падающей тени шара как и в предыдущем случае начинаем с нахождения точки о_Т. Малая ось эллипса, представляющего собой падающую тень, равна отрезку [a_Т b_Т]. Большая полуось – высоте правильного треугольника, построенного на отрезке [a_Т b_Т] Определив точку n_Т, строим точку, ей симметричную относительно оси [a_Т b_Т]. По большой
и малой оси можно построить эллипс различными способами (их около шестисот!), один из которых показан на рис. 38 в правом нижнем углу – способ родственного соответствия. Ввиду того, что этот раздел не изучается студентами в курсе начертательной геометрии, приведем только порядок нахождения случайных точек искомого эллипса.

Рис. 38. Второй способ нахождения теней шара

С центром в точке о_Т построим две окружности, диаметры которых равны большой и малой осям эллипса. Затем через точку о_Т проведем какой-либо луч и отметим точки его пересечения с каждой окружностью.

Из полученных точек проведем прямые, параллельные большой
и малой осям и на их пересечении зафиксируем одну из искомых точек эллипса, На рисунке ниже показано построение одной из таких точек – точки 1_Т. Остальные точки определяются аналогично и соединяются плавной кривой.

В том случае, когда требуется определить собственную тень шара на одном изображении, можно воспользоваться приемом, показанным на рис. 39.

Рис. 39. Построение собственной тенишара по 8-ми точкам

Точки 1,2,…, 8 указывают на последовательность нахождения восьми точек искомого эллипса.

Аналитическое обоснование этому приему существует, но в данной работе не приводится.

Рассмотрим некоторые задачи, связанные с построением теней на поверхности шара.

З а д а ч а 1

Определить тень точки А на поверхности шара (рис. 40).

Решение данной задачи сводится к нахождению точки пересечения светового луча, проведенного через точку А, с поверхностью шара.

Поскольку в задаче не ставится вопрос о нахождении собственных и падающих теней шара, то достаточно определить только точки пересечения светового луча с поверхностью шара.

Задачи такого рода решаются по известному алгоритму:

1. луч заключается в какую-либо плоскость (или поверхность);

2. строится линия пересечения данной поверхности с проведенной плоскостью (или поверхностью) – фигура сечения;

3. определяются искомые точки пересечения луча с построенной фигурой сечения.

Поскольку луч занимает в пространстве общее положение, авторы учебников по начертательной геометрии обычно рекомендуют применять
в этом случае преобразование чертежа (например, метод замены плоскостей проекций), для того чтобы луч или прямая линия заняли в пространстве частное положение, поскольку только в этом случае можно получить точное решение задачи.

Рис. 40. Решение задачи 1

Заметим, что преобразованные чертежи имеют большие достоинства: они легко читаются, их применение позволяет избежать построения лекальных кривых по множеству точек и получить точное решение задачи. Но, к сожалению, преобразованные чертежи занимают большую площадь на поле листа бумаги и потому являются довольно громоздкими.

Известно, что любую задачу по начертательной геометрии можно решить, не прибегая к преобразованию чертежа. Покажем, как в данной задаче обойтись без последнего и в то же время получить точное решение.

Воспользуемся приведенным выше алгоритмом нахождения точки пересечения прямой линии с поверхностью:

1.заключим световой луч, проходящий через точку А, в коническую поверхность вращения, соосную со сферой. За вершину этой поверхности примем точку T (t, t'), лежащую в плоскости главного меридиана сферы. Ось конической поверхности определится парой точек O (o, o') и T (t, t').

Для построения главного меридиана конической поверхности, параллельного плоскости V, применим способ прямоугольного треугольника

(рис. 40), который реализован на графическом условии данной задачи,
а необходимые пояснения к нему приведены на этом же рисунке справа.

После построения очертания конической поверхности перейдем
к выполнению второго пункта алгоритма:

2. найдем линию пересечения данной сферы с проведенной вспомогательной поверхностью;

Обе поверхности сосны по построению, поэтому согласно лемме
о пересечении соосных поверхностей они пересекутся по окружностям столько раз, сколько раз пересекутся их главные полумеридианы. В данном случае пересечение произошло по двум окружностям, которые на фронтальной проекции отобразились отрезками прямых линий (на
рис. 40 показана только одна из них, которая задействована в задаче).

3. Определяем искомые точки пересечения светового луча, принадлежащего конической поверхности, с построенными фигурами сечения (окружностями).

На эпюре зафиксирована только одна точка а_Т' поскольку она является действительной тенью точки А на фронтальной проекции. Горизонтальную проекцию а_Т определим с помощью линии связи на горизонтальной проекции луча, пользуясь свойством принадлежности.

З а д а ч а 2

Построить тень отрезка [AB] на поверхности шара (рис. 41).

Наличие собственной тени для решения поставленной задачи необходимо. Способ ее нахождения изложен ранее. Применять способ обратных лучей для этой задачи нерационально, поскольку по условию не требуется определение падающих теней шара.

Подойдем к решению задачи следующим образом. Из аналитической геометрии известно, что любая плоскость пересекает сферу по окружности. Лучевая плоскость, проходящая через отрезок [AB] – горизонтально-проецирующая, поэтому пересекает сферу по окружности, которая на горизонтальной проекции отобразится отрезком прямой [12].

Рис. 41. Нахождение тени отрезка [AB] на поверхности шара

Поскольку окружность одновременно принадлежит лучевой плоскости и данной сфере ее фронтальная проекция (представляющая собой эллипс) может быть построена по точкам, исходя из условия их принадлежности поверхности сферы. Точке обеспечивается принадлежность сфере с помощью параллели, заведомо на ней лежащей. Горизонтальная проекция параллели отобразится окружностью, фронтальная – отрезком прямой, на котором определяется фронтальная проекция точки. На рис. 41 показаны построения всех характерных точек кривой линии и нескольких случайных, затем все точки соединены плавной кривой.

Точка пересечения светового луча с построенным по точкам эллипсом является действительной тенью точки А на поверхности шара, от которой идет дальнейшее отбрасывание тени отрезка [AB] вплоть до точки
K (k, k'), построенной на этом отрезке способом обратного луча, после того как на фронтальной проекции определена точка k_Т' пересечением контура собственной тени с дугой эллипса. Отрезок [KB] частично отбрасывает тень на поверхность шара в области его собственной тени и на землю (плоскость H) в виде горизонтального следа лучевой плоскости.

6.2.4. Тень произвольного тела вращения

Пусть требуется построить собственные и падающие тени тела вращения с криволинейными образующими.

На рис. 42 изображено тело вращения, состоящее из эллипсоида, плавно переходящего в торовую поверхность.

Рис. 42. Построение теней произвольного тела вращения

Поскольку образующими данных поверхностей являются кривые линии определение контура собственной тени более сложная задача по сравнению с предыдущими случаями. Поступим следующим образом.

Проведем на поверхности данного комплексного тела множество параллелей, плоскости которых параллельны плоскости H (две такие случайные плоскости P и Q отмечены на чертеже). Построим их падающие тени, которые будут представлять собой множество окружностей. Огибающая этих окружностей – контур падающей тени. В данном случае очертание контура может быть построено только приближенно. Отметим точки касания полученного контура с падающими тенями параллелей
а_Т, b_Т,…e_Т.С помощью обратных лучей восстановим точки на поверхности данного тела, которые отбросили эти тени. Соединив их одноименные горизонтальные и фронтальные проекции, получим очертание контура собственной тени.

Рис. 43. Собственные и падающие тени

комплексной поверхности вращения

На рис.43 представлен результат решения задачи.

В некоторых случаях возникает необходимость показать только одно изображение некоторых тел вращения с собственными тенями. Покажем, как это выполнить на примерах конуса, цилиндра и шара, оси которых вертикальны.

Пристроим к фронтальной проекции конуса полуокружность. Через точку 1 проведем прямую, параллельную левой очерковой образующей конуса до пересечения с горизонтальным диаметром в точке 2. Через точку 2 проведем две прямые под углами 45° и – 45° до пересечения с полуокружностью и отметим на ней точки 3 и 5. Из построенных точек опустим перпендикуляры на горизонтальный диаметр, на котором зафиксируем точки 4 и 6. Соединив последние с точкой s' с учетом видимости, получим границу собственной тени конуса на фронтальной проекции (рис. 44, а).

Рис. 44. Собственные тени на телах вращения

Аналогичным образом строятся собственные тени на цилиндре. Поскольку его образующие имеют общую несобственную точку, то точка 2 совпадает с центром окружности (рис. 44, б).

На поверхности шара контуром собственной тени является окружность, отображенная на проекции эллипсом, построенная по восьми точкам (рис 44, в).

Тени фрагментов зданий

Тени в нишах

Напомним, что для построения контура падающей тени оригинала выявляется контур его собственной тени (иногда достаточно определить только элементы контура).

Рассмотрим тени в нишах различной конфигурации. На рис. 45, а изображена прямоугольная ниша. Проведем анализ освещенных и неосвещенных фрагментов ниши и стены. При заданном направлении светового потока стена здания освещена, левая грань – в тени, следовательно, ребро [AB] (столб) является частью контура собственной тени и от него следует строить тень падающую. Поскольку отрезок [AB] параллелен задней стенке

ниши, то согласно выводу, приведенному ранее, падающая тень отрезка [AB] равна и параллельна этому отрезку.

Рис. 45. Тени в нишах:

а – ниша прямоугольной формы;

б – ниша с плоской задней стенкой и цилиндрическим потолком;

в – ниша с задней цилиндрической стенкой и плоским потолком

На фронтальной проекции ниши будет видна только реальная часть этой тени. На нижнюю грань ниши (подоконник) отрезок [AB] отбрасывает тень в виде следа лучевой горизонтально-проецирующей плоскости, проходящего через точку А.

Стена здания и верхняя грань ниши пересекаются по отрезку [BС]. Поскольку эта грань находится в тени, ребро [BС] лежит на границе света и тени, следовательно, оно входит в часть контура собственной тени, от которого построим тень падающую.

Ребро [BС], как и ребро [AB], параллельно задней стенке ниши, поэтому его падающая тень так же равна и параллельна этому отрезку.

У ниши, изображенной на рис. 45, б,в контур собственной тени входит отрезок [AB] и дуга полуокружности, параллельные задней стенке ниши, поэтому падающая тень на эту стенку идентична фигуре контура.

У третьей ниши в контур собственной тени входит отрезок [AB]
и [BС], т.к. по нему пересекается освещенная стена и потолок ниши, находящийся в тени. Кроме того, в собственной тени оказывается часть цилиндрического отсека, выделенная на чертеже более бледным тоном. Лучевая плоскость, проходящая через ребро [AB] пересекает подоконник также как в двух предыдущих случаях, а цилиндрическую стенку ниши по горизонтально-проецирующей прямой, поскольку оно параллельно образующим цилиндра. Лучевая плоскость, проходящая через ребро [BС], равно наклонена к плоскостям проекций H и V. Поскольку это ребро перпендикулярно плоскости W – лучевая плоскость – профильно-проецирующая, поэтому она пересекает цилиндрическую поверхность по эллипсу, который отображается на горизонтальной и фронтальной проекциях окружностями (точнее – одинаковыми симметричными дугами окружностей).

Тень козырька

На рис.46 над прямоугольной нишей в стене изображен козырек.
Построение тени в нише было рассмотрено ранее. Проведем анализ освещенности граней козырька для определения его контура собственной тени. При заданном направлении S освещены верхняя, передняя и левая боковая грань козырька, остальные грани (в том числе и грань, примыкающая
к стене) находятся в тени, следовательно, ребра [ME], [ED], [DC], [CB], [BA] и [AM], входят в состав контура собственной тени козырька.

На этом же рисунке справа дано наглядное изображение контура собственной тени, по которому легко ориентироваться при нахождении падающих теней.

Построим от этого контура падающую тень. Ребро [ME] принадлежит стене, поэтому его тенью является отрезок [m_Т'e_Т']. Ребро [ED] по отношению к стене является гвоздем. Падающая тень гвоздя представляет собой след лучевой фронтально-проецирующей плоскости, определяемый точками e_Т' и d_Т'.

Для получения точки d_Т' через точку D в пространстве проводим луч, параллельный направлению S, а на эпюре отображаем его проекции. Точка пересечения проведенного луча со стеной – падающая тень точки D.

Рис. 46. Тень козырька

Ребро [DC] параллельно стене, поэтому отбрасывает на него тень
в виде равного ему и параллельного отрезка [d_Т'c_Т']. Следующее ребро [CB] также параллельно стене здания, поэтому [b'c']∥[b_Т'c_Т']. Поскольку ребро [BA] гвоздь по отношению к стене, а [BA]∥[ED], то их падающие тени также параллельны между собой [a_Т'b_Т']∥[e_Т'd_Т']. Заметим, что луч, проведенный через точку B, пересекает заднюю стену ниши в точке b_Т', поэтому часть ребер [CB] и [BA] отбрасывают тени на нее.

Тень кронштейна

Пусть дано два изображения кронштейна, у которого требуется найти собственные и падающие тени (рис. 47). Выявим на его поверхности контур собственной тени. Для этого проведем анализ освещенных и неосвещенных поверхностей, ограничивающих кронштейн.

Рис. 47. Построение падающих теней кронштейна

При заданном направлении S освещенными окажутся две передние грани поверхности кронштейна, параллельные плоскости V, ограниченные прямоугольниками (ABCD) и (KLFE); грань, примыкающая к стене, параллельная плоскости H, и левый отсек плоской фигуры, параллельный плоскости W.

Заметим, что при определении контура следует учесть наличие цилиндрической поверхности, часть которой находится в собственной тени
и границей света и тени на ней служит отрезок [KL].

Общий контур собственной тени представляет собой пространственную линию и состоит из отрезков прямых и двух дуг окружностей. Наглядное изображение контура показано на рис. 48.

В этой задаче следует обратить внимание на одну деталь. При определении освещенности отдельных частей поверхности предмета для установления контура собственной тени необходимо иметь в виду такую тонкость, которая в учебной литературе не рассматривается. Заключается она в том, что, устанавливая освещенность плоского отсека, следует давать по этому поводу однозначный ответ (освещена, либо не освещена), поскольку на освещенный участок может упасть тень от фрагмента данного геометрического объекта. Так, в нашем случае, на плоскость прямоугольниками (KLFE) падает тень от верхнего фрагмента кронштейна, но она не влияет на установление контура собственной тени объекта.

Определив полный контур собственной тени объекта, строим тень падающую.

Рассуждения, которые необходимо провести для построения падающей тени, аналогичны тем, которые приведены в предыдущей задаче.

Рис. 48. Наглядное изображение

контура собственной тени