Модель формального кибернетического нейрона.
Формальный нейрон состоит из 3 логических блоков: входы, функция преобразования, выход. Рассмотрим подробнее блок функции преобразования.
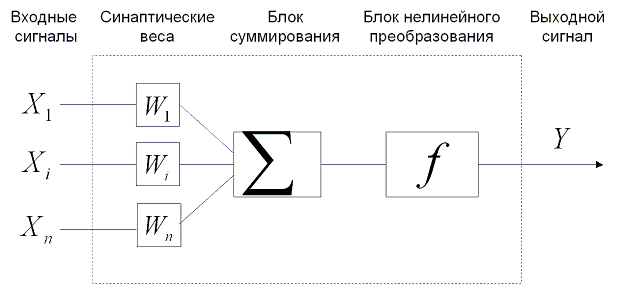
Figure 1. Модель формального нейрона. Пунктирной рамкой выделен блок функции преобразования.
Блок функции преобразования можно так же разделить на части: синаптические веса, блок суммирования, функция нелинейного преобразования.
Итак, опишем алгоритм работы блока функции преобразования:
1. Входные сигналы умножаются на коэффициенты (синаптические веса или просто веса). Для каждого входа - свой коэффициент.
2. Умноженные на веса входы суммируются.
3. Результат суммирования подаётся на вход функции преобразования. Обычно
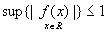 .
.
4. Результат функции подаётся на выход.
В качестве функции преобразование обычно используются следующие:
· простой порог,
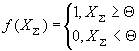
· ленейно-пороговая функция,
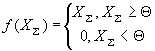
· сигмоида,
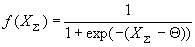
,где Θ - некий фиксированный порог. Следует заметить, что это не полный список, а лишь набор самых популярных вариантов.
Данная модель формально кибернетического нейрона, была предложена Мак-каллоком и Питтсом в 1943 году и встречается во многих нейросетях, но не является догмой. Существуют нейронные сети и с другими моделями нейронов: о них подробнее мы поговорим ниже.
Данные.
Нейронная сеть, как уже говорилось, осуществляет некоторое отображение. Математически, нейросеть работает с векторами, осуществляя отображение из одного пространства в другое, однако в отношение нейросетей принято говорить "образы" или "сигналы". Входные данные принято обычно называть "входные образами" или "входные сигналы", а выходные соответственно - "выходные образы" или "выходные сигналы",. Такая терминология связана с историей возникновения и областью применения нейросетей.
Обучение.
Как мы уже отмечали, для того чтобы нейросеть осуществляла требуемое отображение, т.е. на каждый вектор входных данных создавала требуемый вектор на выходе, требуется её настроить. Обычно процесс настройки называется "обучением" (далее мы всегда будем говорить обучение). Существуют два метода обучения: с наставником и на основе самоорганизации.
Рассмотрим общий для всех сетей принцип обучения с наставником. Пускай имеется некоторый набор пар следующего вида: входной вектор - выход сети (т.е. нам известно как точно должна работать сеть на некотором множестве входных векторов). Такое множество пар называют "обучающая выборка" (далее мы будем использовать именно этот термин). Процесс обучения выглядит следующим образом:
1. Предадим синаптическим весам некоторые начальные значения.
2. Предъявим сети вектор из обучающей выборки.
3. Вычислим отклонения выхода сети от желаемого.
4. По некоторому алгоритму (зависящему от конкретной архитектуры) подстроим синаптические веса, учитывая отклонение полученное на предыдущем шаге.
5. Повторим шаги 2-4 пока сеть не станет выдавать ожидаемый выход на векторах из обучающей выборки или пока отклонение не станет ниже некоторого порога.
Другими словами, подстроим веса сети так, чтобы сеть работала с приемлемой точностью на известных данных. Идея метода состоит в предположении, что при достаточно репрезентативной обучающей выборки, более-менее равномерно покрывающей всё множество возможных входных векторов, обученная нейросеть будет выдавать правильный или близкий к правильному результат на векторах которым её не обучали.
Отметим, что такое предположение вполне закономерно, ведь обученная сеть будет обрабатывать входные вектора схожим образом с векторами из обучающей выборки, следовательно если искомое преобразование в достаточной степени непрерывно и гладко, то результат должен быть вполне удовлетворительным.
Самоорганизация - это свойство небольшого количества нейронных сетей. Под самоорганизацией подразумевается способность сети приспособиться осуществлять желаемое отображение самостоятельно в процессе работы - то есть без обучающей выборки. Обычно такие сети применяются к задачам кластеризации некоторого множества. Для этого метода обучения трудно сформулировать некий общий абстрактный алгоритм, т.к. обычно метод обучения очень сильно зависит от архитектуры конкретной сети.
Далее, при описании конкретных архитектур, мы будем подробно говорить об алгоритмах обучения для каждой конкретной сети.
