Промежуточные и окончательная проверки правильности расчёта

Из пунктов 16.1–16.4 настоящей лекции просматривается следующая последовательность расчёта статически неопределимых систем методом сил:

1. Выбор основной системы.

2. Построение в основной системе метода сил эпюр внутренних усилий от X_j = 1 (j = 1, 2, …, n) и от заданной нагрузки.

3. Вычисление коэффициентов при неизвестных и свободных членов системы канонических уравнений метода сил.

4. Решение системы канонических уравнений.

5. Определение внутренних усилий в заданном сооружении.

Многоэтапность расчёта требует постоянного контроля за ходом решения задачи. В первую очередь, необходимо убедиться в правильности построения эпюр внутренних усилий в основной системе от неизвестных метода сил X_j = 1 (j = 1, 2, …, n) и заданной нагрузки (см. п. 5.2 и 5.4 первой части настоящего курса лекций).

Далее проводится проверка достоверности вычислений коэффициентов при неизвестных и свободных членов системы канонических уравнений. Изложим здесь ход этой проверки для рамных и балочных систем, где коэффициенты при неизвестных и свободные члены вычисляются только сопряжением эпюр изгибающих моментов M₁, M₂, …, M_i, …, M_j, …, M_n, M_F, построенных в основной системе метода сил от Х₁ = 1, Х₂ = 1, …, Х_i = 1, …, Х_j = 1, …, Х_n = 1 и заданной нагрузки. Для проверки используем суммарную эпюру изгибающих моментов:

M_s = M₁ + M₂ + … + M_i + … M_j + …+ M_n. (16.14)

Сопрягая эту эпюру саму на себя, получим сумму всех коэффициентов при неизвестных системы канонических уравнений:

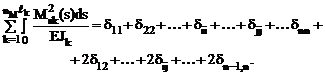(16.15)

В этом нетрудно убедиться, подставив соотношение (16.14) в левую часть формулы (16.15). Если полученная сумма не совпадает с суммой всех коэффициентов при неизвестных, ранее вычисленных по формулам (16.8) и (16.9), то необходимо выявить ошибку путём построчной проверки правильности вычисления коэффициентов при неизвестных метода сил. Эту сумму для i-й строки системы канонических уравнений получим, сопрягая суммарную эпюру изгибающих моментов M_s с эпюрой изгибающих моментов M_i, построенной в основной системе от действия Х_i = 1.

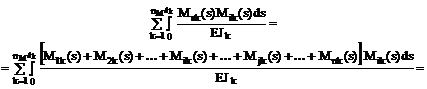
= d_i1 + d_i2 + … + d_ii + … + d_ij + … +d_in. (16.16)

Сумму всех грузовых коэффициентов системы канонических уравнений получим, сопрягая суммарную эпюру изгибающих моментов M_s с грузовой эпюрой изгибающих моментов M_F, полученной в основной системе от заданного силового воздействия.

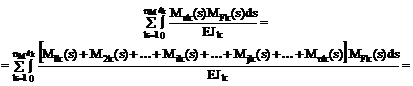
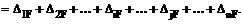(16.17)

Сумма грузовых коэффициентов, полученная из соотношения (16.17), должно совпадать с суммой свободных членов системы канонических уравнений, ранее вычисленных по формуле (16.10).

На заключительном этапе расчёта проводится проверка правильности эпюр внутренних усилий M, Q, N, построенных в заданном статически неопределимом сооружении от внешней нагрузки. Эти эпюры достоверны, если выполнены кинематические условия, а именно: перемещения по направлению любого неизвестного метода сил X_i (i = 1, 2, …, n) в основной системе от действия всех усилий в лишних связях X₁, X₂, …, X_j, …, X_n и заданной нагрузки должно быть равно нулю, так как в заданном сооружении имеется связь, препятствующая перемещению по направлению X_i. Для вычисления этого перемещения проверяемые эпюры внутренних усилий M, Q, N сопрягаются с эпюрами внутренних усилий M_i, Q_i, N_i, полученными в основной системе метода сил от X_i (i = 1, 2, …, n).

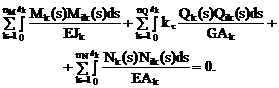(16.18)

В расчётах статически неопределимых рамных и балочных систем эта проверка производится по сокращённой формуле Мора:

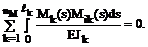(16.19)

Для кинематической проверки правильности расчёта статически неопределимого сооружения могут быть использованы эпюры внутренних усилий, построенные в каких-то других основных системах метода сил от X_i (i = 1, 2, …, n) и ранее не используемых для расчёта заданной системы, а также суммарные эпюры внутренних усилий, полученные в любой основной системе M_s, Q_s, N_s от X_i (i = 1, 2, …, n) (см., например, соотношение (6.14) для M_s).

Пример расчёта статически неопределимой рамы методом сил

Построить эпюры внутренних усилий от силового воздействия в раме, изображённой на рис. 16.10,а, если известно, что изгибная жёсткость поперечных сечений ригелей рамы EJ_p вдвое больше изгибной жёсткости поперечных сечений её стоек EJ_с, т.е. EJ_p : EJ_с = 2 : 1.

1. Определение степени статической неопределимости рамы по формуле "контуров" (14.1).

n_st = 3K – H = 3 × 2 – 4 = 2.

При вычислении n_st учтено, что шарнир правой стойки рамы, соединяющий в узле три диска, эквивалентен двум простым шарнирам.

2. Выбор основной системы метода сил и её кинематический анализ. Основную систему образуем введением цилиндрических шарниров в верхний и нижний узлы правой стойки рамы, т.е. удалением связей, препятствующих взаимному повороту двух соседних сечений верхнего правого узла рамы и повороту сечения, расположенному близко к правому опорному защемлению рамы. За неизвестные метода сил в нашем случае принимаются усилия в удалённых угловых связях, а именно – изгибающие моменты Х₁ и Х₂ (рис. 16.10,б).

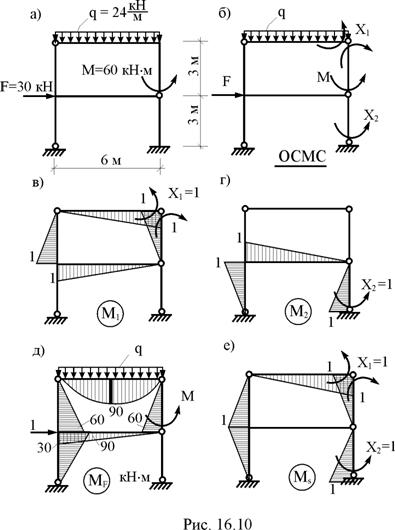
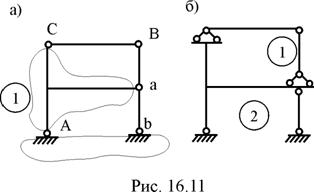
Принятая для расчёта основная система метода сил с кинематической точки зрения имеет простую структуру и геометрически неизменима. Действительно, диск 1 основной системы закрепляется к диску "земля" цилиндрическим шарниром А и связью ab, ось которой не проходит через шарнир А (рис. 16.11,а). К геометрически неизменяемой структуре AbaС узел В присоединён диадой (двумя связями СВ и аВ).

3. Построение эпюр изгибающих моментов в основной системе метода сил от Х₁ = 1 (рис. 16.10,в), Х₂ = 1 (рис. 16.10,г) и заданной нагрузки (рис. 16.10,д). Эти эпюры читателям предлагается построить самостоятельно, приняв во внимание рабочую схему основной системы (рис. 16.11,б), на которой показаны её главная и второстепенная части и определён порядок расчёта.

4. Вычисление коэффициентов при неизвестных и свободных членов системы канонических уравнений:

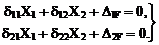
Сопряжение соответствующих эпюр изгибающих моментов будем производить, используя формулу Симпсона и правило Верещагина (см. п. 11.4 второй части настоящего курса лекций). Напоминаем, что определение коэффициентов d_ii, d_ij и D_iF в рамных и балочных системах производится только с учётом изгибных деформаций по формулам (16.8)–(16.10).

Примем EJ_p = 2EJ, EJ_с = EJ (EJ – произвольное число), сохраняя заданное соотношение между изгибными жесткостями поперечных сечений ригелей и стоек рамы.

Читателям рекомендуется тщательно проверить арифметические выражения, записанные ниже для численных значений определённых интегралов формулы Мора.

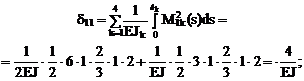
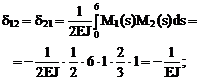
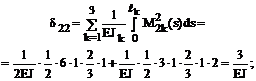
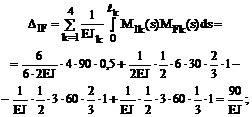
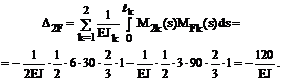
5. Проверка правильности вычисления коэффициентов при неизвестных и грузовых коэффициентов системы канонических уравнений. Суммарная эпюра изгибающих моментов M_s = M₁+M₂ от Х₁ = 1 и Х₂ = 1 в основной системе метода сил показана на рис. 16.10,е.

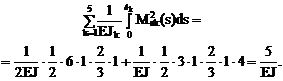
Результат сопряжения эпюры изгибающих моментов M_s саму на себя равен сумме

,

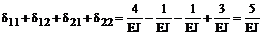что подтверждает достоверность вычисления коэффициентов при неизвестных.

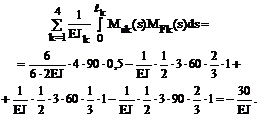
Сумма ранее вычисленных грузовых коэффициентов системы канонических уравнений

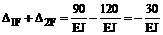
совпадает с результатами сопряжения эпюр изгибающих моментов M_s и M_F, что свидетельствует о правильности их вычисления.

6. Решение системы канонических уравнений:

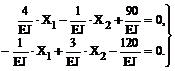
В заданной системе уравнений абсолютное значение жёсткости поперечного сечения стоек рамы EJ_c = EJ сокращается, т.е. величины усилий в лишних связях Х₁ и Х₂ и, следовательно, значения внутренних усилий от заданной нагрузки во всех сечениях рамы зависят от относительного значения изгибных жесткостей поперечных сечений элементов рамы. Этот вывод распространяется на любые статически неопределимые стержневые системы при их расчёте на силовое воздействие.

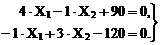
Отсюда получим: Х₁ = -13,64 кН×м, Х₂ = 35,45 кН×м. Знак "минус" для числового значения усилия в лишний связи Х₁ указывает на обратное направление действия этого усилия по сравнению с предварительно принятым при выборе основной системе метода сил.

7. Определение изгибающих моментов в сечениях заданной рамы и построение соответствующей эпюры. Для рассматриваемой задачи соотношение (16.11) примет вид:

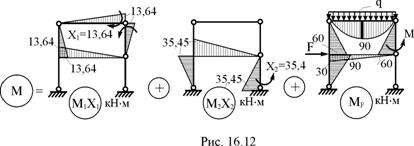
M = M₁X₁ + M₂X₂ + M_F.

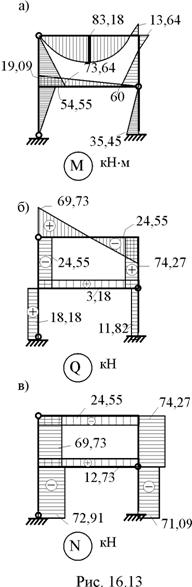
Ординаты эпюры М₁ умножим на –13,64 кН×м, а М₂ – на 35,45 кН×м, затем произведём сложение эпюр М₁Х₁, М₂Х₂ и M_F (рис. 16.12). Эпюра изгибающих моментов заданной раме показана рис. 16.13,а.

8. Кинематическая проверка. Для этой цели используем суммарную эпюру изгибающих моментов M_s (рис. 16.10,е)

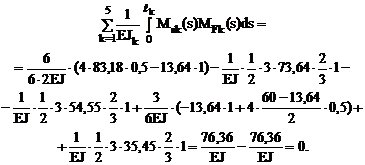
Кинематическая проверка выполнена с нулевой абсолютной погрешностью.

9. Построение эпюр поперечных и продольных сил в заданной раме. Читателям предлагается, используя методику, изложенную в п. 5.4 первой части настоящего курса лекций, эпюру поперечных сил построить по эпюре изгибающих моментов, а эпюру продольных сил – по эпюре поперечных сил. Эпюры Q и N для заданной рамы показаны на рис. 16.13,б,в.