Xlabel('Время, c'), ylabel('Процессы'))
Title('Обучение нейронной сети').
6. Промоделировать сеть ADALINE:
x = sim(net, P);
x1 = cat(1, x{:});
plot(time, x1, 'b', time, p, 'r');
Title('Моделирование нейронной сети').
Лабораторная работа № 8
Исследование радиальных базисных сетей
общего вида
Цель работа: изучение архитектуры радиальных базисных нейронных сетей общего вида и специальных функций для их создания и автоматической настройки весов и смещений, ознакомление с демонстрационными примерами и их скриптами; приобретение навыков построения таких сетей для классификации векторов и аппроксимации функций.
Теоретические сведения
Радиальная, базисная сеть общего вида – это двухслойная нейронная сеть с R входами, каждый из которых может состоять из нескольких элементов. Передаточной функцией нейронов входного слоя является колоколообразная симметричная функция следующего вида:
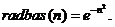
Эта функция имеет максимум, равный 1, при n = 0 и плавно убывает при увеличении n, достигая значения 0.5 при n = ±0.833. Передаточной функцией нейронов выходного слоя является линейная функция perelin.
Функция взвешивания для входного слоя вычисляет евклидово расстояние между каждой строкой матрицы весов и каждым столбцом матрицы входов:
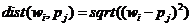 .
.
Затем эта величина умножается на смещение нейрона и поступает на вход передаточной функции, так что
a{i} = radbas(net.prod(dist(net.IW{1, 1}, p).net.b{i})).
Для нейронов выходного слоя функцией взвешивания является скалярное произведение dotprod, а функцией накопления – функция суммирования взвешенных входов и взвешенного смещения netsum.
Для того чтобы понять поведение радиальной базисной сети общего вида, необходимо проследить прохождение вектора входа p. При задании значений элементам вектора входа каждый нейрон входного слоя выдает значение в соответствии с тем, как близок вектор входа к вектору весов каждого нейрона. Таким образом, нейроны с векторами весов, значительно отличающимися с вектором входа p, будут иметь выходы, близкие к 0, и их влияние на выходы линейных нейронов выходного слоя будет незначительное. Напротив, входной нейрон, веса которого близки к вектору p, выдаст значение, близкое к единице.
Для построения радиальных базисных сетей общего вида и автоматической настройки весов и смещений используются две функции newrbeи newrb. Первая позволяет построить радиальную базисную сеть с нулевой ошибкой, вторая позволяет управлять количеством нейронов входного слоя. Эти функции имеют следующие параметры:
net = newrbe(P, T, SPREAD),
net = newrb(P, T, GOAL, SPREAD),
где P – массив размера RxQ входных векторов, причем R – число элементов вектора входа, а Q – число векторов в последовательности;
T – массив размера SxQ из Q векторов цепи и S классов;
SPREAD – параметр влияния, определяющий крутизну функции radbas, значение по умолчания которого равно единице;
GOAL – средняя квадратичная ошибка, при этом значение по умолчанию равно 0.0.
Параметр влияния SPREAD существенно влияет на качество аппроксимации функции: чем больше его значение, тем более гладкой будет аппроксимация. Слишком большое его значение приведет к тому, что для получения гладкой аппроксимации быстро изменяющейся функции потребуется большое количество нейронов: слишком малое значение параметра SPREAD потребует большего количества нейронов для аппроксимации гладкой функции. Обычно параметр влияния SPREAD выбирается большим, чем шаг разбиения интервала задания обучающей последовательности, но меньшим размера самого интервала.
Функция newrbe устанавливает веса первого слоя равным P′, а смещения – равными 0.8326/ SPREAD, в результате радиальная базисная функция пересекает значение 0.5 при значениях евклидового расстояния ±SPREAD. Веса второго слоя LW{2,1} и смещения b{2} определяются путем моделирования выходов первого слоя A{1} и последующего решения системы линейных уравнений:
[LW{2,1} b{2}]*[A{1}; ones] = T.
Функция newrb формирует сеть следующим образом. Изначально первый слой не имеет нейронов. Сеть моделируется и определяется вектор входа с самой большой погрешностью, добавляется нейрон с функцией активации radbas и весами, равными вектору входа, затем вычисляются весовые коэффициенты линейного слоя, чтобы не превысить средней допустимой квадратичной ошибки.
Практические задания
Задание 1. Создать радиальную базисную сеть с нулевой ошибкой для обучающей последовательности P = 0:3 и T = [0.0 2.0 4.1 5.9], проанализировать структурную схему построенной сети и значения параметров ее вычислительной модели, выполнив следующие действия:
1. Создать радиальную базисную сеть с нулевой ошибкой:
P = 0:3;
T = [0.0 2.0 4.1 5.9];
net = newrbe(P, T);
2. Проанализировать структурную схему построенной сети:
gensim(net);
3. Проанализировать параметры вычислительной модели сети:
Net
net.layers{1}.size % – число нейронов в первом слое;
net.layers{2}.size % – число нейронов во втором слое;
net.layers{1}.initFcn
net.layers{1}.netInputFcn
net.layers{1}.transferFcn
net.layers{2}.initFcn
net.layers{2}. transferFcn
net.layers{2}.netInputFcn
net.inputWeights{1, 1}.initFcn
net.inputWeights{1, 1}.weightFcn
net.inputWeights{2, 1}.initFcn
net.inputWeights{2, 1}.weightFcn
net.inputWeights{1, 1}.learnFcn
net.IW{1, 1}, net.b{1}
net.LW{2, 1}, net.b{2}
net.inputWeights{1, 1}, net.biases{1}
net.inputWeights{2, 1}, net.biases{2}
4. Выполнить моделирование сети и построить графики:
plot(P, T, ‘*r’, ′MarkerSize′, 2, ′LineWidth′, 2)
Hold on
V=sim(net, P);
plot(P, V, ′*b′, ′MarkerSize′, 9, ′LineWidth′, 2)
P1=0.5:2.5;
Y=sim(net, P1);
plot(P1, Y, ′*k′, ′MarkerSize′, 10, ′LineWidth′, 2)
Задание 2. Создать радиальную базисную сеть для обучающей последовательности P = 0:3 и T = [0.0 2.0 4.1 5.9] при средней квадратичной ошибке 0.1, проанализировать структурную схему построенной сети и значения параметров ее вычислительной модели, выполнив действия задания и заменив в командах функцию newrbe(P, T) на newrb(P, T, 0.1).
Задание 3. Создать радиальную базисную сеть с нулевой ошибкой для большого числа значений входа и цели, выполнив следующие действия:
1. Задать обучающую последовательность и построить для нее график:
P = -1:0.1:1;
T = [-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 …
0.4609 0.1336 -0.2013 -0.4344 -0.5000 -0.3930…
-0,1647 0.988 0.3072 0.3960 0.3449 0.1816
-0.0312 -0.2189 -0.3201];
plot(P, T, ′*r′, ′MarkerSize′, 4, ′LineWidth′, 2)
Hold on
2. Создать сеть и определить число нейронов в слоях:
net = newrbe(P, T);
net.layers{1}.size % – в первом слое– 21 нейрон;
net.layers{2}.size % – во втором слое– 1 нейрон;
gensim(net);
3. Выполнить моделирование сети и построить график:
V = sim(net, P);
plot(P, V, ′*b′, ′MarkerSize′, 5, ′LineWidth′, 2)
P = [-0.75 -0.25 0.25 0.75]
V = sim(net, P);
Hold on
plot(P, V, ′*b′, ′MarkerSize′, 10, ′LineWidth′, 2).
Задание 4. Создать радиальную базисную сеть для большого числа значений входа и цели при средней квадратичной ошибке 0.01, выполнив действия задания 3 и заменив функцию newrbe(P, T) на функцию newrb(P, T, 0.01).
Задание 5. Провести аппроксимацию функции f(x) с помощью радиальных базисных функций 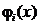 в виде следующего разложения в ряд:
в виде следующего разложения в ряд:
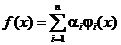 ,
,
здесь коэффициенты разложения по радиальным базисным функциям:
p = -3:0.1:3;
a1 = radbas(P);
a2 = padbas(P-1.5);
a3 = radbas(P+2);
a = a1 + a2 + 0.5*a3;
plot(P, a1, p, a2, p, 0.5*a3, p, a).
Как видно из графика, разложение по радиальным базисным функциям обеспечивает необходимую гладкость. Разложение указанного вида может быть реализовано на двухслойной нейронной сети, первый слой которой состоит из радиальных базисных нейронов, а второй – из единственного нейрона с линейной характеристикой, на котором суммируются выходы нейронов первого слоя.
Задание 6. Исследовать гладкость аппроксимации при следующих значениях параметра SPREAD: 1, 0.01 и 12, используя команды из четвертого задания.
Лабораторная работа № 9
Исследование радиальных базисных сетей
типа GRNN
Цель работы: изучение архитектурных особенностей радиальных базисных нейронных сетей типа GRNN и специальных функций для их создания, автоматической настройки весов и смещений и нормированного взвешивания; ознакомление с демонстрационным примером и его скриптом, а также приобретение навыков построения таких сетей для решения задач обобщенной регрессии, анализа временных рядов и аппроксимации функций.
Теоретические сведения
Радиальная базисная сеть типа GRNN(Generalized Regression Neural Network), или обобщенная регрессионная сеть имеет архитектуру, аналогичную архитектуре радиальной базисной сети общего вида, и отличается от нее структурой второго слоя, в котором используется блок normprod для вычисления нормированного скалярного произведения строки массива весов LW{2,1} и вектора выхода первого слоя а{1} в соответствии со следующим соотношением:
n{2} = LW{2,1} * a{1}/sum(a{1}).
В общем виде функция normprod определяется так:
normprod(W,P) = W * P/sum(P/1),
где W – матрица весов размера S × R,
P – массив входов размера R × Q,
sum(P,1) – сумма элементов массива Р по столбцам.
Создание сети осуществляется фукцией
net = newgrnn(P,T,SPREAD).
Эта функция устанавливает веса первого слоя равным Р′, а смещение – равным величине 0.8326/SPREAD, что приводит к радиальным базисным функциям, которые пересекают величину 0.5 при значениях взвешенных входов ± SPREAD. Веса второго слоя устанавливаются равными Т. Смещения отсутствуют.
Первый слой сети GRNN – это радиальный базисный слой с числом нейронов, равными числу элементов Q обучающего множества. В качестве начального приближения для матрицы весов выбирается массив Р′, смещение для этого слоя устанавливается равным вектор-столбцу с элементами 0.8326/SPREAD. Функция dist вычисляет расстояние между вектором входа и вектором веса нейрона. Вход передаточной функции равен поэлементному произведению взвешенного входа сети на вектор смещения. Входом каждого нейрона первого слоя является значение функции radbas. Если вектор веса нейрона равен транспонированному вектору входа, то взвешенный вход Ра-
вен 0, а выход равен 1. Если расстояние между вектором входа и вектором веса нейрона равно SPREAD, то выход нейрона будет равен 0.5.
Второй слой сети GRNN – это линейный слой с числом нейронов, также равным числу элементов Q обучающего множества, причем в качестве начального приближения для матрицы весов LW{2,1} выбирается массив Т. Если на вход подается вектор Рi, близкий к одному из векторов входа Р из обучающего множества, то этот вектор сгенерирует значение выхода слоя, близкое к единице. Это приведет к тому, что выход второго слоя будет близок к ti.
Если параметр влияния SPREAD мал, радиальная базисная функция характеризуется резким спадом и диапазон входных значений, на который реагируют нейроны входного слоя, оказывается весьма малым. При увеличении этого параметра диапазон увеличивается и выходная функция становится более гладкой.
Практические задания
Задание 1. Создать обобщенную регрессионную сеть для обучающей последовательности Р=0:3 и Т[0.0 2.0 4.1 5.9], проанализировать ее структурную схему и значения параметров вычислительной модели, выполнить моделирование сети для различных входов, построить графики и оценить влияние на выходные значения параметра SPREAD, выполнив следующие команды:
P = 0:3;
T = [0.0 2.0 4.1 5.9];
net = newgrnn(P,T) %–параметр SPREAD = 1.0;
Gensim (net)
plot(P,T, ′*r′, ′MarkerSize′, 2, ′LineWidth′, 2)
Hold on
V = sim(net, P)
plot(P,V, ′o8′, ′MarkerSize′, 8, ′LineWidth′, 2)
P1 = 0.5:2.5;
Y = sim(net, P1);
plot(P1,V, ′+k′, ′MarkerSize′, 10, ′LineWidth′, 2)
Y = sim(net, 0:0.5:3) %–для нового входа;
net = newgrnn(P, T, 0.1) %–параметр SPREAD = 0.1;
Y = sim(net, 0:0.5:3) %–сравнить результаты.
Задание 2. Построить обобщенную регрессионную сеть для решения задачи аппроксимации и экстраполяции нелинейной зависимости, восстанавливаемой по экспериментальным точкам, выполнив следующие команды:
P = [1 2 3 4 5 6 7 8 ]; %–экспериментальные;
T = [0 1 2 3 2 1 2 1 ]; %–данные в 8 точках;
SPREAD = 0.7; %–значение меньше шага Р, равного 1;
net = newgrnn(P, T, SPREAD)
net.layers{1}.size, net.layers{2}.size % - 8 и 8;
A = sim(net, P);
plot(P, T, ′*k′, ′MarkerSize′, 10), hold on
plot(P, A, ′ok′, ′MarkerSize′, 10) %–аппроксимация;
P2 = -1: 0.1: 10; %–диапазон Р2 больше диапазона Р;
A2 = sim(net, P2);
plot(P2, A2, ′-k′, ′LineWidth′, 2) %–экстраполяция;
Hold on,
plot(P, T, ′*k′, ′MarkerSize′, 10) %–сравнить точки.
Лабораторная работа № 10
Исследование радиальных базисных сетей
типа PNN
Цель работы: изучение архитектурных особенностей радиальных базисных нейронных сетей типа PNN и специальных функций для их создания, автоматической настройки весов и смещений и конкурирующей активации; ознакомление с демонстрационным примером и его скриптом; приобретение навыков построения таких сетей для решения задач классификации на основе подсчёта вероятности принадлежности векторов к рассматриваемым классам и для решения других вероятностных задач.
Теоретические сведения
Радиальная базисная сеть типа PNN (Probabilistic Neural
Networks), или вероятностная нейронная сеть, имеет архитектуру, аналогичную архитектуре радиальной базисной сети общего вида, и отличается от неё структурой второго слоя, в котором используются функция взвешивания dotprod (скалярное произведение сигналов и весов), функция накопления netsum и передаточная функция compet – конкурирующая функция, преобразующая вектор входа слоя нейронов таким образом, чтобы нейрон с самым большим входом имел выход, равной единице, а все другие нейроны имели выходы, равные нулю. Смещения используются только в первом слое.
Создание вероятностей сети осуществляется функцией
net=newpnn(P,T,spread),
где Р– массив размераR*Q из Q входных векторов с R элементами;
T– массив размера S*Q из Q векторов цели и S классов;
SPREAD– параметр влияния, значение по умолчанию 1.0.
Для вероятностей сети необходимо задать обучающее множество из Qпар векторов входа и целей. Каждый вектор цели имеет K элементов, указывающих класс принадлежности и, таким образом, каждый вектор входа ставится в соответствие одному из К классов. В результате образуется матрица связанности T размера K*Q, состоящая из нулей и единиц, строки которой соответствуют классам принадлежности, а столбцы – векторам входа. Таким образом, если элемент Т(i,j) матрицы связанности равен единице, то это означает,
чтоj-й входной вектор принадлежит к классу i.
Весовая матрица входного слоя IW формируется как и для радиальной базисной сети общего вида с использованием векторов входа из обучающего множества.
Весовая матрица второго слоя соответствует матрице связан-
ности Т, которая строится с помощью функции ind2vec.
Практические задания
Задание 1. Создать вероятностную нейронную сеть для обучающей последовательности, состоящей из вектора входа Р=[1 2 3 4 5 6 7] и индекса классов Тс=[1 2 3 2 2 3 1], проанализировать её структурную схему и параметры вычислительной модели, выполнить моделирование сети и оценить правильность классификации, выполнив следующие команды:
Р=[1 2 3 4 5 6 7]; %–значения входа;
Tc=[1 2 3 2 2 3 1]; %–индексы классов (3);
T=ind2uec(Tc); %–матрица связанности (целей);
net=newpnn(P,T); %–создание сети PNN;
gensim(net); %–структура сети;
net; %–параметры сети;
Y=sim(net,P); %–моделирование сети;
Yc=iecc2ind(Y); %–классы входных векторов;
% 1 2 3 2 2 3 1.
Задание 2. Создать вероятностную нейронную сеть для определения принадлежности двухэлементных входных векторов к одному из трёх классов на основании обучающей последовательности 7 входов Р[0 0; 1 1; 0 3; 1 4; 3 1; 4 1; 4 3] и индекса классов Тс=[1 1 2 2 3 3 3], значения в котором определяют класс соответствующего вектора входа, выполнив команды:
Р=[0 0; 1 1; 0 3; 1 4; 3 1; 4 1; 4 3 ]’; %–7 векторов.
Тс=[1 1 2 2 3 3 3 ]; %–классы.
T= ind2vec(Tc); %–формирование разряженной матрицы
% связанности;
T= full (T); %–преобразование к полной матрице;
net= newpnn; %–создание вероятностной сети;
net.layers {1}.size %–число нейронов 1-го слоя;
net.layers {2}.size %–число нейронов 2-го слоя;
Y= sim (net, P); %–моделирование сети;
Yc= vec2ind(Y); %–формирование индекса классов;
Pt= [1 3; 0 1; 5 2]’; %–векторы для тестирования;
A= sim (net, Pt); %–тестирование сети;
Ac= vec2ind (A); %–формирование индекса классов.
Задание 3. Проанализировать структурные схемы, значения параметров вычислительных моделей и результаты моделирования нейронных сетей, используемых в следующих демонстрационных примерах:
Demorb1– рациональные базисные сети;
Demorb3– использование не перекрывающихся функций активации (передаточных функций);
Demorb4– использование перекрывающихся передаточных функций;
Demogrn1– аппроксимация функций с помощью сети типа GRNN;
Demogrn1– классификация векторов с помощью сети типа PNN.
Для анализа использовать скрипты примеров.
Лабораторная работа № 11
Исследование самоорганизующихся
слоев Кохонена
Цель работы: изучение архитектуры самоорганизующихся нейронных слоев Кохонена и специальных функций для их создания, инициализации, взвешивания, накопления, активации, настройки весов и смещений, адаптации и обучения; ознакомление с демонстрационными примерами и их скриптами, а также приобретение навыков построения самоорганизующихся слоев для исследования топологической структуры данных, их объединением в кластеры (группы) и распределением по классам.
Теоретические сведения
Самоорганизующийся слой Кохонена – это однослойная нейронная сеть с конкурирующей передаточной функцией compet, которая анализирует выходные значения нейронов слоя и выдаёт в качестве результата наибольшее из этих значений (значение нейрона-победителя).
Инициализация весов входов производится с помощью функции средних значений
W = midpoint (S,PR),
где S – число нейронов в слое Кохонена;
PR– матрица размера Rx2, задающая диапазоны 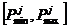 изменения R элементов входного вектора;
изменения R элементов входного вектора;
W– матрица весов размера SxR для входов слоя, столбцы которой имеют значения 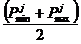 .
.
Инициализация весов смещений нейронов слоя производится с помощью функции равных смещений
B = initcon(S,PR),
которое каждому нейрону задаёт одно и то же смещение, равное exp(1)*S. Например, для S=5 это смещение равно 5*2.71828= =1.359740*101.
Взвешивание входов слоя Кохонена реализуется в виде отрицательного евклидова расстояния между каждой строкой Wiматрицы весов W и каждым столбцом Pj матрицы входов P, которое вычисляется функцией negdist(W,P). Суммирование взвешенных входов со смещениями производится функцией netsum.
Формирование самоорганизующегося слоя Кохонена осуществляется функцией
net = newc(PR,S,KLr,clr),
где KLr – параметр функции настройки весов, значение по умолчанию которого равно 0.01;
clr – параметр функции настройки смещений, значение по умолчанию которого равно 0.001.
Эта функция формирует однослойную сеть с R нейронами и R входами. Веса входов устанавливаются равными половине диапазона соответствующего вектора входа для всех нейронов. Также для всех нейронов устанавливается одно и то же смещение, равное e*s. Выходы нейронов поступают на конкурирующую передаточную функцию compet, которая определяет победителя. Номер активного нейрона-победителя I* определяет ту группу (кластер), к которой наиболее близок входной вектор.
Для того чтобы сформированная таким образом сеть решала задачу кластеризации данных, необходимо предварительно настроить ее веса и смещения по обучающей последовательностью векторов с помощью функций настройки learnk и learncon соответственно, используя процедуру адаптации adapt или процедуру обучения train.
Функция learnk рассчитывает приращение весов dW в зависимости от вектора входа P, выхода а, весов w и параметра скорости настройки lr в соответствии с правилом Кохонена:
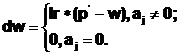
Таким образом, вектор веса, наиболее близкий к вектору входа, модифицируется так, чтобы расстояние между ними стало ещё меньше. Результат такого обучения заключается в том, что победивший нейрон, вероятно, выиграет конкуренцию и в том случае, когда будет представлен новый входной вектор, близкий к предыдущему, и его победа менее вероятна, когда будет представлен вектор, существенно отличающийся от предыдущего. Когда на вход сети поступает всё большее и большее число векторов, нейрон, являющийся ближайшим, снова корректирует свой весовой вектор w. В конечном счёте, если в слое имеется достаточное количество нейронов, то каждая группа близких векторов окажется связанной с одним из нейронов слоя. В этом и заключается свойство самоорганизации слоя
Кохонена.
Одно из ограничений всякого конкурирующего слоя состоит в том, что некоторые нейроны оказываются незадействованными, или “мертвыми”. Это происходит оттого, что нейроны, имеющие начальные весовые векторы, значительно удаленные от векторов входа, никогда не выигрывают конкуренции, независимо от продолжительности обучения. Для ликвидации нечувствительности таких нейронов используют положительные смещения, которые добавляются к отрицательным расстояниям удаленных нейронов. Функция learncon производит такую корректировку смещений следующим образом.
В начале процедуры настройки сети всем нейронам присваивается одинаковый характер активности C0 = 1/S. В процессе настройки эта величина для активных нейронов увеличивается, а для неактивных нейронов уменьшается:
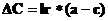 .
.
Нетрудно убедиться, что для всех нейронов, кроме нейрона-
победителя, приращения отрицательны. Функция learcon рас-
считывает приращения вектора смещений следующим образом: 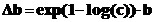 .
.
Увеличение смещений для неактивных нейронов позволяет расширить диапазон покрытия входных значений, и неактивный нейрон начинает формировать кластер, что улучшает кластеризацию входных данных.
Практические задания
Задание 1. Создать слой Кохонена для двух векторов входа, проанализировать его структурную схему и параметры вычислительной модели, произвести обучение сети и моделирование, выполнив следующие команды:
P = [.1 .8 .1 .9; .2 .9 .1 .8]; %–для обучения слоя;
net = newc([01;01],2); %–создание слоя;
gensim (net); %–структура слоя;
net = train(net,P); %–обучение слоя;
w = net.Iw{1,1}; %–веса после обучения;
b =net.b{1}; %–смещение после обучения;
plot(P(1,:),P(2,:),’+k’)
title (′Векторы входа′),xlabel(′P(1,:)′), ylabel(′P(2,:)′)
Hold on
plot (w, ′or′)
P1= [0.2:0.1:0.7; 0.2:0.1:0.7];
y = sim(net,P1)
yc = vec2ind(Y)
Задание 2. Создать слой Кохонена, который для 48 случайных векторов формирует 8 кластеров, выполнив следующие команды:
c = 8; %–число кластеров;
n =6; %–число векторов в классе;
x = [-10 10; -5 5]; %–диапазон входов;
[r,q] = size(x); %–r число строк; q – число столбцов;
minU = min(x′)′ %–минимальные значения;
maxU = max(x′)′ %–максимальные значения;
v = rand(r,c)*((maxv - minU)*ones(1,c)+minU*ones(1,c));
t = c*n %–число точек;
v = [v v v v v v]; %–48 двухэлементных векторов;
v =v+randn(r,t)*d; %–координаты точек;
P = v; %–векторы с отклонениями (нормальный закон);
plot (P(1,:),P(2,:), ′+k′)
title (‘Векторы входа’),xlabel(′P(1,:)′), ylabel(′P(2,:) ′)
net =newc([-2 12; -1 6],8 0.1);
wo = net.IW{1,1} %–веса после инициализации;
bo = net.b{1} %–смещения после инициализации;
co = exp(1)/60 %–начальная активность;
net.trainParam.epochs = 500; %–обучение;
net = train(net, P) , a = sim(net, P), ac = vec2ind(a)
net.IW{1} %–веса после обучения;
bn = net.b{1} %–смещения после обучения;
cn = exp(1)/bn %–активность после обучения;
net = newc([-2 12; -1 6], 8 0.1);
co = exp(1). /net.b{1} %–начальная активность;
net.adaptParam.passes = 500;
[net, y,e] = adapt (net, mat2cell(p)) % – адаптация;
a = sim(net, P) %–моделирование после
ac = vec2ind(a) % адаптации.
Задание 3. Построить график приращений вектора смещений и проанализировать пример democ1.
Задание 4. С помощью слоя Кохонена произвести кластеризацию оценок абитуриентов.
Лабораторная работа № 12
Исследование самоорганизующихся
карт Кохонена
Цель работы: изучение архитектуры самоорганизующихся нейронных сетей в виде карт Кохонена и специальных функций для создания карты и её топологии, взвешивания, накопления, настройки весов (размещение нейронов), адаптации и обучения; ознакомление с демонстрационными примерами и их скриптами, а также приобретение навыков построения самоорганизующихся карт для решения задач кластеризации входных векторов.
Теоретические сведения
Cамоорганизующаяся карта Кохонена – это однослойная нейронная сеть без смешения с конкурирующей функцией compet, имеющая определенную топологию размещения нейронов в N-мерном пространстве. В отличие от слоя Кохонена карта Кохонена после обучения поддерживает такое топологическое свойство, когда близким входным векторам соответствуют близко расположенные активные нейроны.
Первоначальная топология размещения нейронов в карте Кохонена формируется при создание карты с помощью функции newsom, одним из параметров которого является имя топологической функции gridtop, nextop или randtop, что соответствует размещению нейронов в узлах либо прямоугольной, либо гексагональной сетки, либо в узлах сетки со случайной топологией.
Расстояния между нейронами и векторами входов вычисляются с помощью следующих функций:
dist – евклидово расстояние d=sqrt((posi-pj).^2);
boxdist – максимальное координатное смещение d=max(abs(posi-pj));
mandist – расстояние суммарного координатного смещения d=sum(abs(posi-pj));
linkdist – расстояние связи

Формирование саморганизующейся карты Кохонена осуществляется функцией
net=newsom(PR,[d1, d2,…],tfcn, dfсn, olr, osteps, tlr, tnd)),
где Pr – массив размера R*2 минимальных значений векторов входа;
d1,d2…– число нейронов по i-йразмерности карты. По умолчанию – двумерная карта с числом нейронов 5*8;
tfсn – функция топологии карты, по умолчанию nextop;
dfcn – функция расстояния, по умолчанию linkdist;
olr – параметр скорости обучения на этапе размещения, по умолчанию 0.9;
osteps – число циклов обучения на этапе подстройки, по умолчанию 1000;
tlr – параметр скорости на этапе подстройки, по умолчанию 0.02;
tnd – размер окрестности на этапе подстройки, по умолчанию 1.
Настройка карты Кохонена производится по каждому входному вектору независимо от того, применяется метод адаптации или метод обучения. В любом случае функция learnsom выполняет настройку карты нейронов.
Прежде всего определяется нейрон-победитель и корректируется его вектор весов и векторы соседних нейронов согласно соотношению
dw=lr*A2*(p′ – w),
где lr – параметр скорости обучения, равный olr для этапа упорядочения нейронов и tlr для этапа подстройки;
A2 – массив соседства для нейронов, расположенных в окрестности нейрона-победителя i:
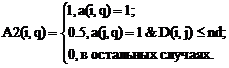
Здесь а(i,q) – элемент выхода нейронной сети;
D(i,j) – расстояние между нейронами i и j;
nd – размер окрестности нейрона-победителя.
Таким образом, вес нейрона-победителя изменяется пропорционально половинному параметру скорости обучения, а веса соседних нейронов – пропорционально половинному значению этого параметра.
Весь процесс обучения карты Кохонена делится на два этапа:
А) этап упорядоченности векторов весовых коэффициентов в пространстве признаков;
Б) этап подстройки весов нейронов по отношению к набору векторов входа.
На этапе упорядочения используется фиксированное количество шагов. Начальный размер окрестности назначается равным максимальному расстоянию между нейронами для выбранной топологии и затем уменьшается до величины, используемой на следующем этапе, и вычисляется по следующей формуле:
nd=1.00001+(max(d)-1)(1-s/S),
где max(d) – максимальное расстояние между нейронами; s– номер текущего шага, а S – количество циклов на этапе упорядочения.
Параметр скорости обучения изменяется по правилу
lr =tlr+(olr-tlr)(1-s/S).
На этапе подстройки, который продолжается в течение оставшейся части процедуры обучения, размер окрестности остается постоянным и равным
nd=tnd+0.00001,
а параметр скорости обучения изменяется по следующему правилу
lr= tlr*S/s.
Параметр скорости обучения продолжает уменьшаться, но очень медленно. Малое значение окрестности и медленное уменьшение параметра скорости обучения хорошо настраивают сеть при сохранении размещения, найденного на предыдущем этапе. Число шагов на этапе подстройки должно значительно превышать число шагов на этапе размещения. На этом этапе происходит тонкая настройка весов нейронов по отношению к набору векторов входов.
Нейроны карты Кохонена будут упорядочиваться так, чтобы при равномерной плотности векторов входа нейроны также были распределены равномерно. Если векторы входа распределены неравномерно, то и нейроны будут иметь тенденцию распределяться в соответствии с плотностью размещения векторов входа.
Таким образом, при обучении карты Кохонена решается не только задачи кластеризации входных векторов, но и выполняется частичная классификация.
Практические задания
Задание 1. Рассчитать положение нейронов на четырехмерной сетке с прямоугольной топологией размера 5*4*3*2 и сделать попытку построить график расположения нейронов, выполнив следующие команды:
pos=gridtop(5,4,3,2) %–массив координат узлов размера N*S,
% где N – количество измерений, равное 4,
% а 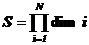 – количество узлов сетки,
– количество узлов сетки,
% равное произведению числа нейронов по
% каждому измерению 5*4*3*2=120;
plotsom(pos) % – вывод только трех размерностей.
Задание 2. Рассчитать положение нейронов на двухмерной сетке с прямоугольной топологией размера 3*2 и построить график расположения нейронов, выполнив следующие команды:
рos =gridtop(2,3) % 0 1 0 1 0 1
% 0 0 1 1 2 2
plotsom(pos) % – плоский график.
Задание 3. Рассчитать положение нейронов на двухмерной сетке с прямоугольной топологией размера 3*2 и построить график расположения нейронов, выполнив следующие команды:
рos =gridtop(3,2) % 0 1 0 1 0 1
% 0 0 1 1 2 2
plotsom(pos) % – плоский график.
Задание 4. Рассчитать положение нейронов на трехмерной сетке с гексагональной топологией размера 5*4*3 с 60 нейронами и построить график их расположения, выполнив следующие команды:
рos =Hextop(5,4,3) %– массив размера 3*60;
рlotsom(pos) %–построение графика.
Задание 5. Сформировать гексагональную сетку размером 2*3 и построить график, выполнив команды:
pos=hextop(2,3) % 0 1.0 0.5 1.5 0 1.0
% 0 0 0.866 0.866 1.7321 1.7321
Plotsom(pos)
Задание 6. Создать сетку размера 2*3 со случайным расположением узлов и построить график расположения нейронов, выполнив следующие действия:
pos=randtop(2,3) % 0.062 0.647 0.49 и т. д.
% 0 0.122 0,904 и т. д.
plotsom(pos) %–построение графика.
Задание 7. Создать сетку размера 5*4*3 со случайным расположением узлов и построить график расположения нейронов, выполнив следующие действия:
pos=randtop(5,4,3) % – создание сетки ;
plotsom(pos) %–построение графика.
Задание 8. Вычислить евклидово расстояние между нейронами сети с теологией, для которой задана матрица для 10 нейронов в трехмерном пространстве, выполнив следующие команды:
pos=rand(3,10) %–случайная матрица координат;
d=dist(pos) %–евклидово расстояние между нейронами.
Задание 9. Вычислить расстояние максимального смещения координат нейронов, размещенных в трехмерном пространстве, выполнив команды:
pos = rand(3,10); %–случайная матрица координат
d = boxdist(pos) %–максимальное координатное смещение,
% которые для векторов х и–у вычисляются
% следующим образом: d = max(abs(x-y)).
Задание 10. Вычислить суммарные координатные смещения для сетки из 10 нейронов в трехмерном пространстве со случайной матрицей координат, выполнив следующие действия:
pos = rand(3,10) %–случайные координаты для 10 нейронов.
d = mandist(pos) %–суммарные координатные смещения,
% которые для векторов х и–у вычисляются
% следующим образом: d = sum(abs(x-y)).
Задание 11. Вычислить расстояние связи между нейронами, распределёнными случайным образом в трехмерном пространстве, выполнив следующие команды:
pos = rand(3,10) %–массив случайных координат
для 10 % нейронов.
d = linkdist(pos) %–расстояния связи между нейронами,
% определяемые следующим образом:
% – 0 1 1 1 1 1 1 1 1 1 1 1
% – 1 0 1 1 1 1 1 1 1 1 1 1
% – 1 1 0 1 1 1 1 1 1 1 1 1
% – 1 1 1 0 2 1 2 1 1 1 1 1 и т. д.
Задание 12. Создать гексагональную карту Кохонена разме-
ром 2х3, проанализировать ее структурную схему и параметры вычислительной модели, произвести обучение карты и ее моделирование, а также построить необходимые графики, выполнив следующие команды:
net = newsom([0 2; 0 1],[2 3]); % – два входа.
net, net.layers{1} % – вычислительная модель.
P = [0.1 0.3 1.2 1.1 1.8 1.7 0.1 0.3 1.2 1.1 1.8 1.7;…….
0.2 0.1 0.3 0.1 0.3 0.2 1.8 1.8 1.9 1.9 1.7 1.8];
plotsom(net.IW{1,1}, net.layers{1}.distances)
Hold on
plot(P(1,:),P(2,:),′*k′,′MarkerSize′,10)
net.trainParam.epochs = 2000;
net.trainParam.show = 100;
net = train(net,P);
plot(P(1,:),P(2,:),′*′,′MarkerSize′,10)
Hold on
plotsom(net.IW{1,1}, net.layers{1}.distances)
net.IW{1,1}
a = sim(net,[1.5;1] % – a = (3,1) 1.
Задание 13. Создать одномерную карту Кохонена из 10 нейронов, обучить её на последовательности из 100 двухэлементных векторов единичной длины, распределенных равномерно в пределах от 0
до 90º, построить график распределения векторов по кластерам и выполнить моделирование сети для одного вектора входа, выполнив следующие команды:
аngels=0 : 0.5 +pi/99 : 0.5*pi;
p=[sin(angels); cos(angels)];
plot(P(1, 1:10:end), P(2, 1:10:end), ′*8′)
Hold on
net=newsom([0 1 ;0 1], [10]);
net.trainparam.epochs=2000;
net.trainparam.show=100;
[net,tr]=train(net,P);
plotsom(net.iw{1,1}, net.laye
