Искусственные нейронные сети

Цель работы: изучение архитектуры искусственных нейронных сетей, способов их графического изображения в виде функциональных и структурных схем и программного представления в виде объектов специального класса network, включающих массив структур с атрибутами сети и набор необходимых методов для создания, инициализации, обучения, моделирования и визуализации сети, а также приобретение навыков построения сетей различной архитектуры с помощью инструментального программного пакета Neural Network Toolbox системы MATLAB.

Теоретические сведения

Хотя отдельные нейроны и способны после некоторой процедуры обучения решать ряд задач искусственного интеллекта, все же для эффективного решения сложных задач по распознаванию образов, идентификации и классификации объектов, распознаванию и синтезу речи, оптимальному управлению применяют достаточно большие группы нейронов, образуя из них искусственные нейронные сети в виде связанных между собой слоёв, напоминающие биологические нейронные (нервные) сети человека и животных.

Существует множество способов организации искусственных нейронных сетей, которые могут содержать различное число слоёв нейронов. Нейроны могут быть связаны между собой как внутри отдельных слоёв, так и между слоями. В зависимости от направления передачи сигнала эти связи могут быть прямыми или обратными. Слой нейронов, непосредственно принимающий информацию из внешней среды, называется входным слоем, а слой, передающий информацию во внешнею среду, – выходным слоем. Остальные слои, если они имеются в сети, называются промежуточными, или скрытыми. В ряде случаев такого функционального распределения слоёв сети не производится, так что входы и выходы могут присоединяться к любым слоям и иметь произвольное число компонент.

Структура, или архитектура сети искусственных нейронов зависит от той конкретной задачи, которую должна решать сеть. Она может быть однослойной без обратных связей или с обратными связями, двухслойной с прямыми связями, трехслойной с обратными связями и т. д. Сети с обратными связями называют часто рекуррентными.

Описание архитектуры искусственной нейронной сети помимо указания числа слоёв и связей между ними должно включать сведения о количестве нейронов в каждом слое, виде функций активации в каждом слое, наличии смещений для каждого слоя, наличии компонент входных, выходных и целевых векторов, а в ряде случаев и характеристики топологии слоёв. Например, для аппроксимации любой функции с конечным числом точек разрыва широко используется сеть с прямой передачей сигналов. В этой сети имеется несколько слоёв с сигмоидальными функциями активации. Выходной слой содержит нейроны с линейными функциями активации. Данная сеть не имеет обратных связей, поэтому её называют сетью с прямой передачей сигналов (FF-net).

Графически искусственная нейронная сеть изображается в виде функциональной или структурой схемы. На функциональной схеме сети с помощью геометрических фигур изображаются её функциональные блоки, а стрелками показываются входы, выходы и связи. В блоках и на стрелках указываются необходимые обозначения и параметры.

Структурная схема сети изображается с помощью типового набора блоков, соединительных элементов и обозначений, принятых в инструментальном программном пакете Neural Network Toolbox системы MATLAB и пакете имитационного моделирования Simulink той же системы. Структурная схема сети может быть укрупнённой или детальной, причём степень детализации определяется пользователем. Системы обозначений блоков, элементов и параметров сети является векторно-матричной, принятой в системе MATLAB. Если в обозначении используется два индекса, то, как правило, первый индекс (индекс строки) указывает адресата, или пункт назначения, а второй индекс (индекс столбца) – источник структурной схемы сети. Структурные схемы создаются системой автоматически с помощью команды gensim. Если элементом вектора или матрицы на структурной схеме является сложный объект, то используются соответственно ячейка и массив ячеек.

Программным представлением, или вычислительной моделью искусственной нейронный сети, является объект специального класса network, который включает массив структур с атрибутами сети и набор методов, необходимых для создания сети, а также для её инициализации, обучения, моделирования и визуализации. Класс Network имеет два общих конструктора, один из которых не имеет параметров и обеспечивает создание массива структур с нулевыми значениями полей, а второй – имеет минимальный набор параметров для создания модели нейронной сети, достраиваемой затем до нужной конфигурации с помощью операторов присваивания. Для создания нейронных сетей определённого вида используются специальные конструкторы.

Практические задания

Задание 1. Создать вычислительную модель нейронной сети с двумя выходами, тремя слоями и одним целевым входом, используя общий конструктор сети с параметрами

Net = network (numInputs, numLayers, biasConnect, imputConnect, layerConnect, outputConnect, tartegtConnect).

Связи между слоями должны быть только прямыми, входы необходимо соединить с первым слоем, а выход – с последним. Выход должен быть целевым, первый слой должен иметь смещения.

Смысл и значения параметров конструктора для создания модели сети заданной архитектуры таковы:

numImputs=2 – количество входов сети;

numLayers=3 – количество слоёв в сети;

biasConnect=[1; 0; 0] – матрица связности для смещений размера numLayers * 1;

inputConnect=[1 1; 0 0; 0 0] – матрица связности для входов размера numLayers * numImputs;

layerConnect=[0 0 0;1 0 0 0 ; 0 1 0] – матрица связности для слоёв размера numLayers * numLayers;

outputConnect=[0 0 1] – матрица связности для выходов размера 1* numLayers;

targetConnect=[0 0 1] – матрица связности для целей размера 1 * numLayers.

Порядок выполнения заданий следующий:

1. Создать шаблон сети, выполнив команду

net = network (2, 3, [1; 0; 0], [1 1; 0 0 ; 0 0], …. ,

[0 0 0 ; 1 0 0 ; 0 1 0], [0 0 1])

2. Проверить значения полей вычислительной модели нейронной сети net и их соответствие заданным значениям в списке параметров.

3. Проверить значения вычисляемых полей модели, которые дополняют описание архитектуры сети

numOutputs = 1 – количество выходов сети;

numTargets = 1 – количество целей сети;

numInputDelays = 0 – максимальное значение задержки для входов сети.

numLayersDelays = 0 – максимальное значение задержки для слоёв сети.

Заметим, что каждый выход и каждая цель присоединяются к одному или нескольким слоям при этом количество компонент выхода или цели равно количеству нейронов в соответствующем слое. Для увеличения возможности модели в сеть включают линии задержки либо на её входах, либо между слоями. Каждая линия задерживает сигнал на один такт. Параметры numInputDelays и NumLayerDelays определяют максимальное число линий для какого-либо входа или слоя соответственно.

4. Проанализировать структурную схему построенной сети, выполнив команду gensim(net) и детализируя блоки с помощью двойного щелчка левой клавиши мыши по рассматриваемому блоку. На структурных схемах искусственных нейронных сетей в пакете NNT используются следующие обозначения:

а) Neural Network – искусственная нейронная сеть с обозначениями входов p{1}, p{2}, …и выхода y{1};

б) входы Input1 , или p{1} и Input2 , или p{2};

в) дисплей y{1};

г) Layer 1, Layer 2, Layer 3, … слои нейронов с обозначениями входов p{1}, p{2], a{1}, a{2}, … и выходов a{1}, a{2}, a{3}, … , y{1};

д) TDL – линии задержки (Time Delay) с именами Delays1,
Delays2, ..., которые обеспечивают задержку входных сигналов или сигналов между слоями нейронов на 1, 2, 3, … такта;

е) Weights – весовая матрица для входных сигналов или сигналов между слоями нейронов; размер матрицы весов для каждого вектора входа S´R, где S – число нейронов входного слоя, а R – число компонент вектора входа, умноженное на число задержек; размер матрицы для сигналов от слоя j к слою i равен S´R,гдеS – число нейронов в слое i, а R – число нейронов в слое j, умноженное на число
задержек;

ж) dotprod – блок взвешивания входных сигналов и сигналов между слоями, на выходе которого получается сумма взвешенных, т. е. умноженных на соответствующие веса компонент сигнала;

з) mux – концентратор входных сигналов и сигналов между слоями, преобразует набор скалярных сигналов в вектор, а набор векторов в один вектор суммарной длины;

и) netsum – блок суммирования компонент для каждого нейрона слоя: компонент от нескольких векторов входа с учётом задержек, смещения и т. п.;

к) hardlim, purelin и т. д. – блоки функций активации;

л) pd{1, 1}, pd{1, 2}, ad{2, 1}, ... – сигналы после линий задержки (d - delay);

м) iz{1, 1}, iz{1, 2}, lz{2, 1}, lz{3, 2} – вектор-сигналы с выхода концентратора;

н) bias – блок весов смещений для слоя нейронов;

о) IW – массив ячеек с матрицами весов входов: IW{i, j} – матрицы для слоя i от входного вектора j;

п) LW – массив ячеек с матрицами весов для слоёв: LW{i, j} – матрицы для слояi от слоя j.

5. Проанализировать все параметры каждого блока структурной схемы рассматриваемой нейронной сети и в случае необходимости обратиться к справочной системе пакета NNT.

6. Задать нулевые последовательности сигналов для входов

P = [0 0 ; 0 0]

и произвести моделирование сети

A = sim(net, P).

7. Задать диапазоны входных сигналов и весовые матрицы с помощью следующих присваиваний:

net.inputs{1}.range = [0 1];

net.inputs{2}.range = [0 1];

net.b{1} = - ¼;

net.IW{1, 1} = [0.5];

net.IW{1, 2} = [0.5];

net.LW{2, 1} = [0.5];

net.LW{3, 2} = [0.5].

Исполнить команду gensim(net) и проверить параметры блока.

8. Вывести на экран поля вычислительной модели и их содержимое, используя функцию celldisp. Убедиться в правильности значений полей модели.

9. Промоделировать созданную статическую сеть, т. е. сеть без линий задержки, используя групповое и последовательное представление входных сигналов

PG = [0.5 1 ; 1 0.5];

PS = {[0.5 1] [1 0.5]};

AG = sim(net, PG);

AS = sim(net, PS).

Убедиться, что для статической сети групповое и последовательное представления входных сигналов дают один и тот же результат.

10. Дополнить архитектуру созданной нейронной сети линиями задержки для входных сигналов и для сигналов между 2-м и 3-м слоями, превратив таким образом статическую сеть в динамическую:

net.inputWeights{1, 1}.delays = [0 1];

net.inputWeights{1, 2}.delays = [0 1];

net.layerWeights{3, 2}.delays = [0 1 2].

Построить структурную схему динамической сети и выяснить смысл используемых операторов присваивания.

11. Скорректировать весовые матрицы:

net.IW{1, 1} = [0.5 0.5];

net.IW{1, 2} = [0.5 0.25];

net.LW{3, 2} = [0.5 0.25 1].

12. Промоделировать динамическую сеть, используя групповое и последовательное представление входных сигналов:

AG = sim(net, PG);

AS = sim(net, PS).

Убедиться, что групповое представление входных сигналов искажает результат, так как в этом случае работа одной сети заменяется параллельной работой двух (по числу последовательностей) одинаковых сетей с нулевыми начальными значениями сигналов на выходах линий задержки.

13. Вывести на печать поля вычислительной модели и их содержимое, используя функцию celldisp.

14. Сохранить содержимое командного окна в М-файле для последующего использования.

Задание 2. Создать точно такую же динамическую сеть asgnet, используя конструктор класса network без параметров и задавая значения соответствующих полей вычислительной модели с помощью операторов присваивания. Убедиться в идентичности сетей net и asgnet. Сравнить результаты работы полученных сетей.

Задание 3. Используя блоки имитационного моделирования инструментального пакета Simulink системы MATLAB, построить модель динамической сети asgnet, провести исследование модели, проверить адекватность её поведения поведению модели net и оформить электронный отчёт с помощью генератора Report Generator.

Задание 4. Используя конструктор класса network с параметрами и операторы присваивания для полей и ячеек объектов этого класса, построить, выдать на экран и промоделировать искусственные нейронные сети следующей архитектуры:

а) однослойная сеть с тремя нейронами, тремя двухкомпонентными входами и одним целевым выходом;

б) трёхслойная сеть с прямой передачей сигналов и с тремя нейронами в каждом слое; количество входов – три с двумя, пятью и тремя компонентами; для всех слоёв имеется смещение; выход –один;

в) трёхслойная сеть, в которой каждый слой соединён со всеми остальными; вход – один и состоит из двух компонентов; количество нейронов в каждом слое – три; слои имеют смещения;

г) трёхслойная динамическая сеть с тремя нейронами в каждом слое; число входов – три, из них каждый состоит из трёх компонентов; имеются смещения на всех слоях; линии задержки задерживают сигналы на один и два такта и включены между всеми слоями, а также на входе;

д) квадратная сеть с десятью слоями и десятью нейронами в каждом слое; десять векторов подключаются по одному к каждому слою; имеется десять выходов от всех слоёв сети; смещения подключены к каждому слою.

Лабораторная работа № 5

Методы и алгоритмы обучения
искусственных нейронных сетей

Цель работы: изучение и приобретение навыков практического применения методов и алгоритмов инициализации и обучения искусственных нейронных сетей, а также овладение способами их разработки.

Теоретические сведения

После того как сформирована архитектура нейронной сети, должны быть заданы начальные значения весов и смещений, или иными словами, сеть должна быть инициализирована. Такая процедура выполняется с помощью метода init для объектов класса network. Оператор вызова этого метода имеет вид:

net = init (net).

Перед вызовом этого метода в вычислительной модели сети необходимо задать следующие свойства:

net.initFcn – для определения функций, которые будут использоваться для задания начальных матриц весов и весов слоёв, а также начальных векторов смещений;

net.layers {i}. initFcn – для задания функции инициализации i-го слоя;

net.biases{i}.initFcn – для задания начального вектора смещения
i-го слоя;

net.inputWeights{i,j}.initFcn – для задания функции вычисления матрицы весов к слою i от входа j;

net.layerWeight{i,j}.initFcn – для задания функции вычисления матрицы весов к слою i от входа j;

net.initParam – для задания параметров функций инициализации.

Способ инициализации сети определяется заданием свойств и net.initFcn net.layers{i}.initFcn. Для сетей с прямой передачей сигналов по умолчанию используется net.initFcn = ‘initlay’, что разрешает для каждого слоя использовать собственные функции инициализации, задаваемые свойством net.layers{i}.initFcn с двумя возможными значениями: ‘initwb’ и ’initnw’.

Функция initwb позволяет использовать собственные функции инициализации для каждой матрицы весов и для каждого вектора смещений, при этом возможными значениями для свойств net.inputWeights{i,j}.initFcn и net.layerWeight{i,j}.initFcnявляются: ‘initzero’, ‘midpoint’, ’randnc’, ’rands’, а для свойства net.biases{i}.initFcn – значения ‘initcon’, ‘initzero и ‘rands’. Для
сетей без обратных связей с линейными функциями активации
веса обычно инициализируются случайными значениями из интервала [-1 1].

Функция initnwреализуют алгоритм Nguyen-Widrow и применяется для слоёв, использующих сигмоидальные функции активации. Эта функция генерирует начальные веса и смещения для слоя так, чтобы активные области нейронов были распределены равномерно относительно области входов, что обеспечивает минимизацию числа нейронов сети и время обучения.

Другими возможными значениями свойства net.initFcn являются: ‘initcon’, ‘initnw’, ‘initwb’ и ‘initzero’.

Помимо функции initnw следующие функции производят непосредственную инициализацию весов и смещений:

initzero присваивает матрицам весов и векторам смещений нулевые значения;

rands присваивает матрицам весов и векторам смещений случайные значения из диапазона [-1 1];

randnr присваивает матрице весов случайные нормированные строки из диапазона [-1 1];

randnc присваивает матрице весов случайные нормированные столбцы из диапазона [-1 1];

midpoint присваивает элементам вектора смещения начальные равные смещения, зависящие от числа нейронов в слое, и используется вместе с функцией настройки learncon.

Таким образом, задание функций инициализации для вычислительной модели нейронной сети является многоступенчатым и выполняется по следующему алгоритму:

1. Выбрать для свойства net.initFcn одно из возможных значений: ‘initzero’, ‘initcon’, ‘initnw’, ‘initwb’ или ‘initlay’.

2. Если выбраны значения ‘initzero’, ‘initcon’ или ‘initnw’, то задание функций инициализации сети завершено.

3. Если выбрано значение ‘initwb’, то переход к шагу 6.

4. Если выбрано значение ‘initlay’, то переходим к слоям и для каждого слоя i свойству net.layers{i}.initFcn необходимо задать одно из возможных значений: ‘initnw’ или ‘initwb’.

5. Если для i-го слоя выбрано значение ‘initnw’, то для этого слоя задание функций инициализации завершено.

6. Если для всех слоев сети или для какого-то слоя установлено свойство ‘initwb’, то для этих слоёв необходимо задать свойства net.biases{i}.initFcn, выбрав его из набора: ‘initzero’, ‘rands’ или ‘initcon’, а также свойства net.layerWeights{i,j}.initFcn, используя следующие значения: ‘initzero’, ‘midpoint’, ‘randnc’, ‘randnr’или ‘rands’.

Заметим, что с помощью оператора revert(net) можно возвратить значения весов и смещений к ранее установленным значениям.

После инициализации нейронной сети её необходимо обучить решению конкретной прикладной задачи. Для этих целей нужно собрать обучающий набор данных, содержащий интересующие признаки изучаемого объекта, используя имеющийся опыт. Сначала следует включить все признаки, которые, по мнению аналитиков и экспертов, являются существенными; на последующих этапах это множество, вероятно, будет сокращено. Обычно для этих целей используются эвристические правила, которые устанавливают связь между количеством необходимых наблюдений и размером сети. Обычно количество наблюдений на порядок больше числа связей в сети и возрастает по нелинейному закону, так что уже при довольно небольшом числе признаков, например 50, может потребоваться огромное число наблюдений. Эта проблема носит название "проклятие размерности". Для большинства реальных задач бывает достаточно нескольких сотен или тысяч наблюдений.

После того как собран обучающий набор данных для проектируемой сети, производится автоматическая настройка весов и смещений с помощью процедур обучения, которые минимизируют разность между желаемым сигналом и полученным на выходе в результате моделирования сети. Эта разность носит название "ошибки обучения". Используя ошибки обучения для всех имеющихся наблюдений, можно сформировать функцию ошибок или критерий качества обучения. Чаще всего в качестве такого критерия используется сумма квадратов ошибок. Для линейных сетей при этом удаётся найти абсолютный минимум критерия качества, для других сетей достижение такого минимума не гарантируется. Это объясняется тем, что для линейной сети критерий качества, как функция весов и смещения, является параболоидом, а для других сетей – очень сложной поверхностью в N+1-мерном пространстве, где N – число весовых коэффициентов и смещений.

С учётом специфики нейронных сетей для них разработаны специальные алгоритмы обучения. Алгоритмы действуют итеративно, по шагам. Величина шага определяет скорость обучения и регулируется параметром скорости настройки. При большом шаге имеется большая вероятность пропуска абсолютного минимума, при малом шаге может сильно возрасти время обучения. Шаги алгоритма принято называть эпохами или циклами.

На каждом цикле на вход сети последовательно подаются все обучающие наблюдения, выходные значения сравниваются с целевыми значениями и вычисляется функция критерия качества обучения – функция ошибки. Значения функции ошибки, а также её градиента используются для корректировки весов и смещений, после чего все действия повторяются. Процесс обучения прекращается по следующим трём причинам, если:

а) реализовано заданное количество циклов;

б) ошибка достигла заданной величины;

в) ошибка достигла некоторого значения и перестала уменьшаться.

Во всех этих случаях сеть минимизировала ошибку на некотором ограниченном обучающем множестве, а не на множестве реальных входных сигналов при работе модели. Попытки усложнить модель и снизить ошибку на заданном обучающем множестве могут привести к обратному эффекту, когда для реальных данных ошибка становится ещё больше. Эта ситуация называется явлением переобучения нейронной сети.

Для того чтобы выявить эффект переобучения нейронной сети, используется механизм контрольной проверки. С этой целью часть обучающих наблюдений резервируется как контрольные наблюдения и не используется при обучении сети. По мере обучения контрольные наблюдения применяются для независимого контроля результата. Если на некотором этапе ошибка на контрольном множестве перестала убывать, обучение следует прекратить даже в том случае, когда ошибка на обучающем множестве продолжает уменьшаться, чтобы избежать явления переобучения. В этом случае следует уменьшить количество нейронов или слоёв, так как сеть является слишком мощной для решения данной задачи. Если же, наоборот, сеть имеет недостаточную мощность, чтобы воспроизвести зависимость, то явление переобучения скорее всего наблюдаться не будет и обе ошибки – обучения и контроля – не достигнут требуемого уровня.

Таким образом, для отыскания глобального минимума ошибки приходится экспериментировать с большим числом сетей различной конфигурации, обучая каждую из них несколько раз и сравнивая полученные результаты. Главным критерием выбора в этих случаях является контрольная погрешность. При этом применяется правило, согласно которому из двух нейронных сетей с приблизительно равными контрольными погрешностями следует выбирать ту, которая проще.

Необходимость многократных экспериментов ведёт к тому, что контрольное множество начинает играть ключевую роль в выборе нейронной сети, т. е. участвует в процессе обучения. Тем самым его роль как независимого критерия качества модели ослабляется, поскольку при большом числе экспериментов возникает риск переобучения нейронной сети на контрольном множестве. Для того, чтобы гарантировать надёжность выбираемой модели сети, резервируют ещё тестовое множество наблюдений. Итоговая модель тестируется на данных из этого множества, чтобы убедиться, что результаты, достигнутые на обучающем и контрольном множествах, реальны. При этом тестовое множество должно использоваться только один раз, иначе оно превратится в контрольное множество.

Итак, процедура построения нейронной сети состоит из следующих шагов:

1. Выбрать начальную конфигурацию сети в виде одного слоя с числом нейронов, равным половине общего количества входов и выходов.

2. Обучить сеть и проверить ее на контрольном множестве, добавив в случае необходимости дополнительные нейроны и промежуточные слои.

3. Проверить, не переобучена ли сеть. Если имеет место эффект переобучения, то произвести реконфигурацию сети.

Для того чтобы проектируемая сеть успешно решала задачу, необходимо обеспечить представительность обучающего, контрольного и тестового множества. По крайней мере, лучше всего постараться сделать так, чтобы наблюдения различных типов были представлены равномерно. Хорошо спроектированная сеть должна обладать свойством обобщения, когда она, будучи обученной на некотором множестве данных, приобретает способность выдавать правильные результаты для достаточно широкого класса данных, в том числе и не представленных при обучении.

Другой подход к процедуре обучения сети можно сформулировать, если рассматривать её как процесс, обратный моделированию. В этом случае требуется подобрать такие значения весов и смещений, которые обеспечивали бы нужное соответствие между входами и желаемыми значениями на выходе. Такая процедура обучения носит название процедуры адаптации и достаточно широко применяется для настройки параметров нейронных сетей.

По умолчанию для сетей с прямой передачей сигналов в качестве критерия обучения используется функционал, представляющий собой сумму квадратов ошибок между выходами сети и их целевыми значениями:

,

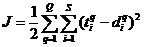где Q – объём выборки; q– номер выборки; i– номер выхода;
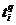– целевое значение для i-го выхода выборки q; 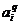– сигнал на i-м выходе при подаче входных сигналов q-й выборки. Целью обучения сети является минимизация этого функционала с помощью изменения весов и смещений.

В настоящее время разработано несколько методов минимизации функционала ошибки на основе известных методов определения экстремумов функций нескольких переменных. Все эти методы можно разделить на три класса:

а) методы нулевого порядка, в которых для нахождения минимума используется только информация о значениях функционала в заданных точках;

б) методы первого порядка, в которых используется градиент функционала ошибки по настраиваемым параметрам, использующий частные производные функционала;

в) методы второго порядка, в которых используются вторые производные функционала.

Для линейных сетей задача нахождения минимума функционала (параболоида) сводится к решению системы линейных уравнений, включающих веса, смещения, входные обучающие значения и целевые выходы и, таким образом, может быть решена без использования итерационных методов. Во всех остальных случаях надо использовать методы первого или второго порядка.

Если используется градиент функционала ошибки, то

,

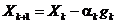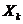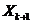где и – векторы параметров на k-й и k+1-й итерациях;
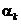– параметр скорости обучения; 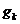– градиент функционала, соответствующий k-й итерации.

Если используется сопряжённый градиент функционала, то на первой итерации направление движения 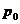выбирают против градиента 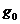этой итерации:

.

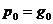Для следующих итераций направление 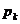выбирают как линейную комбинацию векторов 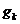и :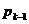

,

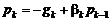а вектор параметров рассчитывают по формуле:

,

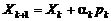Для методов второго порядка расчет параметров на k-м шаге производят по формуле (метод Ньютона):

,

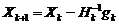где H_k – матрица вторых частных производных целевой функции (матрица Тессе); g_k – вектор градиента на k-й итерации. Вычисление матрицы Тессе требует больших затрат машинного времени, поэтому её заменяют приближенными выражениями (квазиньютоновские алгоритмы).

Градиентными алгоритмами обучения являются:

GD – алгоритм градиентного спуска;

GDM – алгоритм градиентного спуска с возмущением;

GDA – алгоритм градиентного спуска с выбором параметра скорости настройки;

Rprop – пороговый алгоритм обратного распространения ошибки;

GDX – алгоритм градиентного спуска с возмущением и адаптацией параметра скорости настройки.

Алгоритмами, основанными на использовании метода сопряженных градиентов, являются:

CGF – алгоритм Флетчера–Ривса;

CGP – алгоритм Полака–Ребейры;

CGB – алгоритм Биеле–Пауэлла;

SCG – алгоритм Молера.

Квазиньютоновскими алгоритмами являются:

DFGS – алгоритм Бройдена, Флетчера, Гольдфарба и Шанно;

OSS – одношаговый алгоритм метода секущих плоскостей (алгоритм Баттини);

LM – алгоритм Левенберга–Марквардта;

BR – алгоритм Левенберга–Марквардта с регуляризацией по Байесу.

В процессе работы алгоритмов минимизации функционала ошибки часто возникает задача одномерного поиска минимума вдоль заданного направления. Для этих целей используется метод золотого сечения GOL, алгоритм Брента BRE, метод половинного деления и кубической интерполяции HYB, алгоритм Чараламбуса CHA и алгоритм перебора с возвратом BAC.

Практические задания

Задание 1. Адаптировать параметры однослойной статической линейной сети с двумя входами для аппроксимации линейной зависимости вида 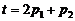, выполнив следующие действия:

1. С помощью конструктора линейного слоя

net = newlin(PR, s, id, lr),

где PR – массив размера Rx2 минимальных и максимальных значений для R векторов входа; s – число нейронов в слое; id – описание линий задержек на входе слоя; lr – параметр скорости настройки, сформировать линейную сеть:

net = newlin([-1 1; -1 1], 1, 0, 0).

2. Подготовить обучающие последовательности в виде массивов ячеек, используя зависимости 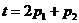и четыре пары значени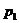й и 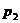(произвольные):

P = {[-1; 1] [-1/3; 1/4] [1/2; 0] [1/6; 2/3]};

T = { -1 -5/12 1 1 }.

3. Для группировки представления обучающей последовательности преобразовать массивы ячеек в массивы чисел:

P1 = [P{:}], T1 = [T{:}].

4. Выполнить команды net и gensim(net), проанализировать поля вычислительной модели и структурную схему сети и записать в тетрадь значения полей, определяющих процесс настройки параметров сети (весов и смещений):

net.initFcn – функция для задания начальных матриц весов и векторов смещений;

net.initParam – набор параметров для функции initFcn, ко-
торые можно определить с помощью команды help(net.initFcn), где initFcn – заданная функция инициализации: initcon, initlay, initnw, initnwb, initzero;

net.adaptFcn – функция адаптации нейронной сети, используемая при вызове метода adapt класса network: adaptwb или trains;

net.adaptParam – параметры функции адаптации, определяемые с помощью команды help(net.adaptFcn);

net.trainFcn – функция обучения нейронной сети, используемая при вызове метода train класса network: trainb, trainbfg, traingbr, trainc, traincgb, traincgt, traincgp, trainngd, traingda, traingdm, traingdx, trainlm, trainoss, trainr, trainrp, trainscg;

net.trainParam – параметры функции обучения, определяемые с помощью команды help(net.trainFcn);

net.performFcn – функция оценки качества обучения, используемая при вызове метода train: mae, mse, msereg, sse;

net.performParam – параметры функции оценки качества обучения, определяемые с помощью команды help(net.performFcn);

net.layers{1}.initFcn – функция инициализации параметров слоя: initnw, initwb;

net.layers{1}.transferFcn – функция активации, которая для
линейного слоя должна быть purelin;

net.layers{1}.netInputFcn – функция накопления для слоя:
netprod, netsum;

net.biases{1}.initFcn – функция инициализации вектора смещений: initcon, initzero, rands;

net.biases{1}.lean – индикатор настройки: 0 – с помощью методаadapt, 1 – с помощью метода train;

net.biases{1}.learnFcn– функция настройки вектора смещений: learncon, learngd, learngdm, learnnp, learnwh;

net.biases{1}.learnParam – параметры функции настройки, определяемые с помощью команды help.(net.biases{1}.learnFcn);

net.inputWeights{1, 1}.initFcn – функция инициализации весов входа: initzero, midpoint, randnc, randnr, rands;

net.inputWeights{1,1}.learn – индикатор настройки: 0 – с помощью метода adapt, 1 – с помощью метода train;

net.inputWeights{1,1}.learnFcn – функция настройки весов: learngd, learngdm, learnhd, learnis, learnk, learnlv1, learnlv2,
learnos, learnnp, learnpn, learnsom, learnnwh;

net.inputWeights{1,1}.learnParam – параметры функции настройки, определяемые с помощью команды help(net.inputWeights {1,1}. learnParam);

net.inputWeights{1,1}.weightFcn – функция для вычисления взвешенных входов для слоя: dist, dotprod, mandist,negdist, normprod;

для многослойных сетей параметры net.inputWeights{i,j}, связанные с обучением такие, как initFcn, learn, learnFcn, learnParam, weightFcn, имеют тот же смысл и могут принимать такие же значения, что и соответствующие параметры для net.inputWeights{1,1}.

5. Выполнить один цикл адаптации сети с нулевым параметром скорости настройки:

[net1, a, e,] = adapt(net, P, T,);

net1.IW{1,1} % – матрица весов после адаптации;

a % – четыре значения выхода;

e % – четыре значения ошибки.

6. Инициализировать нулями веса входов и смещений и задать параметры скорости настройки для них соответственно 0.2 и 0:

net.IW{1} = [0 0];

net.b{1} = 0;

net.inputWeights{1,1}.learnParm.lr = 0.2;

net.biases{1}.learnParam.lr =0.

Нулевое значение параметра скорости настройки для смещения обусловлено тем, что заданная зависимость 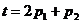не имеет постоянной составляющей.

7. Выполнить один цикл адаптации с заданным значением параметра скорости адаптации:

[net1, a, e] = adapt (net, P, T);

net1.IW{1,1} % – значения весов в сети net1 изменились;

a % – четыре значения выхода сети net1;

e % – четыре значения ошибки сети net1.

8. Выполнить адаптацию сети net с помощью 30 циклов:

for i = 1:30,

[net, a{i}, e{i}] = adapt(net, P, T);

W(i, :) = net.IW{1,1};

end;

cell2mat(a{30}) % – значения выхода на последнем цикле;

cell2mat(e{30}) % – значение ошибки на последнем цикле;

W(30, :) % – веса после 30 циклов;

mse(cell2mat(e{30}) % – функция ошибок: 0.0017176.

Здесь cell2mat – функция преобразования массива числовых ячеек в массив чисел, а mse– функция среднеквадратичной ошибки.

9. Построить графики зависимости значений выходов сети и весовых коэффициентов, а также среднеквадратичной ошибки от числа циклов, используя функцию subplot для деления экрана на окна:

Subplot(3,1,1)

for i = 1:1:30, plot(i, cell2mat(a{i}), ′k′),

Hold on

end;

xlabel(′′), ylabel(′Выходы a(i)′)

Grid

Subplot(3,1,2)

Наши рекомендации