Виражи на автомобильных дорогах.

На кривых, радиусы которых меньше 3000 м для автомобильных дорог 1 категории и 2000 м для других категорий, устраивают виражи, придавая дорожному полотну односкатный поперечный профиль с накло­ном к центру кривой (рис. 78).

Односкатный профиль сохраняется на всем протяжении круговой кривой. Отгон виража делается на переходных кри­вых или на прямых участках, примыкающих к закруглению.

При радиусе кривой, меньшем 700 м, на виражах делают дополнительное уширение проезжей части. Величина этого уширения на две полосы движения в зависимости от радиуса кривой приведена ниже.

Поперечный уклон проезжей части на вираже зависит от радиуса кривой и колеблется от 20 до 60 %.

Поперечный профиль дороги в начале отгона виража имеет вид, показанный на рис. 79, а. В конце отгона виража (в на­чале круговой кривой) дорожное полотно будет иметь одно-

скатный уклон (рис. 79, б). При этом если поворот дорожного полотна осуществляется вокруг его внутренней кромки, про­фильные отметки которой остаются неизменными, то превыше­ние в отметках характерных точек поперечного профиля отно­сительно начального сечения без учета продольного уклона до­роги будет для осевой точки

Рис. 80. Левоповоротный съезд

При пересечении авто­дороги и железной дороги в одном уровне острый угол между их осями должен быть не менее 60°. Подходы автодороги к переезду на протяжении 50 м проекти­руют с продольным укло­ном не более 30 %■

Автодороги 1 категории с дорогами всех категорий, дороги 2 категории с доро­гами 2 и 3 категорий, а также важнейшие дороги 3 категории пересекаются в разных уровнях с устройством пу­тепровода и съездов.

Радиусы кривых левоповоротных съездов должны быть не менее 60—50 м, правоповоротных — не менее 250 м (дороги 1 и 2 категорий) и 125 м (дороги 3 категории).

На всех однопутных съездах устраивают вираж с уклоном 20—60 %. Продольный уклон дорог на подходах к путепроводу и на съездах проектируют не более 40 %• Наименьшие радиусы вертикальных выпуклых кривых принимают на левоповоротных съездах для дорог 1 и 2 категорий 1500 м, на правоповоротных съездах — 5000 м; для вогнутых кривых—1200 и 2000 м соот­ветственно.

На дорогах 1 и 2, а иногда и 3 категории на въездах проек­тируют переходно-скоростные полосы разгона и торможения, в пределах которых машина набирает скорость при выезде на магистраль или, наоборот, снижает скорость для выезда на съезд. Длина полос разгона составляет 150—200 м, торможе­ния 100—75 м; их ширина принимается равной полосе движе­ния основной дороги (3,5 м) с обочиной в 1,5 м при длине от­гона 80—60 м.

Для составления проекта пересечения и расчета элементов съездов производят съемку в масштабе 1:1000—1:2000 с вы­сотой сечения рельефа 0,5—1 м участка, достаточного для раз­мещения всех частей пересечения, и измеряют в натуре углы между осями пересекающихся дорог.

На рис. 80 ОМ и ОМ'— оси автомагистралей, АР и АР'— оси переходно-скоростных полос. Для разбивки левоповоротного съезда необходимо на местности определять положение то­чек В и В' начала и конца круговой кривой съезда и центра кривой С. Так как в точках В и В' прямые участки полосы перпенди­кулярны к радиусу кривой, то из прямоугольных треуголь­ников ABC и АВ'С имеем

где r — величина радиуса петли; 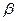— угол пересечения осей дорог.

Следовательно, отложив вдоль осей переходно-скоростных полос расстояния АВ и АВ', найдем на местности точки В и В', от которых разбивают кривую на петлях съезда. Разбивка кри­вой производится методом координат по частям. Для этого де­лят угол на четыре части и в таблицах кривых по аргумен­там r и /4 находят элементы каждой части кривой.

Иногда в месте сопряжения переходно-скоростной полосы и петли съезда вставляют переходную кривую. При небольшом радиусе r кривая ВВ' может быть разбита непосредственно из центра С.

Для разбивки правоповоротного соединения находят поло­жение углов поворота F и F'.

Из прямоугольного треугольника OEF

Расстояние составляет OE=OA + AD + DE, а

где / — расстояние между осями магистрали и переходно-ско­ростной полосы. Отрезок AD получают из выражения

Отрезок DE назначают из условия свободного размещения половины земляного полотна левого съезда В, половины по­лотна соединения правого поворота В' и некоторого запаса D на устройство кювета, т. е.

Вычислив по формулам расстояния OF и ОЕ и найдя в натуре положения точек F и F', из них как вершин углов поворота разбивают кривые. Элементы кривых находят по радиусу R, который желательно иметь не менее 600 м, и по углу поворота, равному 90°— 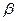/2.

Отложив от начала кривой М вдоль тангенса величину t и ординату 1/2, находят К — точку перехода с правого поворота на скоростную полосу. Из треугольника KC'G получают

Пересечение автомобильных дорог 1—3 категорий с желез­ными дорогами проектируется в разных уровнях. При изыска­ниях дорог 4, 5 категорий также стремятся найти варианты, исключающие пересечение железной дороги в одном уровне.

Разбивка соединений и парков железнодорожных путей. Примыкания, как и любые соединения железнодорожных путей, осуществляют при помощи стрелочных переводов, которые стремятся устраивать на прямых участках пути.

Основными частями стрелочного перевода являются ост­ряки 2 (рис. 81) с переводным механизмом /, переводная кри­вая 3 и крестовина 5. Угол а между рабочими гранями кресто­вины называется углом крестовины. Выражение 2tg( /2) назы­вают маркой стрелочного перевода и обозначают через 1/N. Вследствие малости угла

Точка 4 пересечения граней крестовины называется математи­ческим центром кресто­вины (МЦК). Наиболее распространена марка стрелочных переводов l/W=l/9 (a = 6°20'25") и l/N=l/ll (a=5° 40"). Пересечение осей двух соединяющих путей на­зывается центром стре­лочного перевода (ДСП). Расстояние а от центра стрелочного перевода до начала стрелки и b до конца крестовины, а так­же до других частей стандартны для стрелоч­ного перевода на оси пути, относительно него легко разместить все ча­сти перевода. Отсюда следует вывод, что при разбивке стрелочного перевода на местности необходимо фик­сировать положение его центра.

Для разбивки примыкания трассируемого пути CL (рис.82) к существующему АК находят точку пересечения осей путей В и измеряют угол примыкания 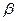. Так как стрелочный перевод отклоняет путь на постоянный угол , то чтобы соединить пути CL и ВК, необходимо разместить его центр не в вершине угла примыкания В, а в некоторой точке А. Расстояние АВ = х мо­жет быть найдено из решения треугольника ABC, в котором известны все три угла: , 180°— 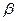, 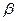— и сторона AC = b + q + T,

где угол и величина Ь определяются по марке стрелочного перевода; угол 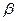измеряют на местности, прямая вставка за­дается, тангенс Т берут из таблиц кривых по углу поворота 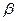— и принятому радиусу R или вычисляют:

Отложив по оси пути от точки примыкания В отрезок х, находят точку А — центр стрелочного перевода, которую закреп­ляют створной плоскостью. Для нахождения на местности по­ложения вершины угла поворота С откладывают вдоль трасси­руемой линии расстояния ВС — 1, величина которого определя­ется из треугольника ABC:

Эту же точку можно получить, если в центре стрелочного перевода построить угол крестовины а и вдоль стороны АС по­лученного угла отложить расстояние b + q + T.

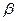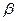Угол поворота трассы в вершине С равен — . Таким обра­зом общий угол примыкания путей с учетом угла отклонения, который задает стрелочный перевод, будет равен сумме углов и — , т. е. равен углу .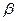

Если место установки стрелочного перевода задано службой движения, то в этом случае разбивка примыкания произво­дится в обратном порядке. Сначала в заданном центре стре­лочного перевода А откладывают угол а, соответственно марке принятой стрелки, затем находят точку С пересечения найден­ного направления с разбитой трассой и измеряют угол пово­рота.

При примыкании параллельных путей расстояние от центра стрелочного перевода А (рис. 83) до вершины угла поворота С

Рис. 83. Примыкание параллельных путей

где / — расстояние между осями путей (например, при l= 5,30 м и стрелке 1/N= 1/9 х = 5,30-9 = 47,70 м).

Угол поворота в точке С в этом случае равен углу кресто­вины а и, следовательно, тангенс кривой следующим

Прямая вставка q может быть найдена по формуле