Исполнительная съемка подкрановых путей.
Исполнительная съемка выполняется в два этапа: предварительная — после монтажа рельсов, и окончательная — после обкатки путей краном. В результате исполнительной съемки определяют и показывают на чертеже фактическое положение в плане и по высоте левого и правого рельса, расстояние между осями рельсов, составляют продольные профили обоих рельсов, подписывают проектные расстояния и отметки, уклонения от них.
Высотное положение рельсов определяют в условных отметках, прокладывая замкнутый нивелирный ход IV класса по обоим рельсам. Нивелир устанавливают на подкрановой балке или на кронштейнах, иногда — на кране, расположенном в середине пролета. Во всех случаях необходимо строго выполнять поверку главного условия нивелира и при больших длинах визирного луча вводить поправки в отсчеты за непараллельность визирной оси и оси уровня. Для проверки прямолинейности рельса теодолит центрируют над его осью в одном конце пролета, визируют на середину рельса в другом конце пролета и по специальной реечке или марке, нуль которых совмещается с осью рельса в каждой контролируемой точке, определяют уклонение оси рельса от створа. Определение выполняют на всех поперечных осях пролета через 6 или 12 м, в тех же точках, для которых определялись отметки при нивелировании.
Прямолинейность второго рельса определяют путем промеров от первого рельса между их осями либо также с помощью теодолита. Для этого в начале и в конце пролета (для контроля ив середине) тщательно откладывают от первого створа проектное расстояние между осями и от этого створа определяют уклонения оси второго рельса. Принято считать уклонение от створа внутрь пролета со знаком «минус», а уклонения в сторону колонны — со знаком «плюс». В этом случае фактическое расстояние между осями рельсов в каждом поперечном сечении вычисляется как разность между проектным расстоянием и алгебраической суммой уклонений рельсов от створов.
Для одновременного контроля рельса в плане и по высоте применяют лазерные приборы и марки, перемещающиеся вдоль рельса. На марке нанесена координатная сетка, позволяющая по перемещению светового луча относительно исходного положения, считывать отклонения оси рельса от створа и от горизонтали.
ГЛАВА 8
ГЕОДЕЗИЧЕСКИЕ РАБОТЫ ПРИ СТРОИТЕЛЬСТВЕ
ЛИНЕЙНЫХ СООРУЖЕНИЙ
8.1. РАЗБИВКА КРИВОЛИНЕЙНЫХ ЭЛЕМЕНТОВ СООРУЖЕНИИ
Общие сведения о кривых
При строительстве автомобильных и железных дорог, трамвайных путей, магистральных трубопроводов, каналов возникает необходимость в разбивке различных кривых: окружности, эллипса, параболы, радиоидальной кривой, кубической параболы, лемнискаты и т. п. Окружность применяется в качестве основной кривой на дорогах и каналах, эллипс—на регуляционных дамбах, конусах насыпи мостовых опор; парабола'—для очертания вертикального продольного профиля дорог, поперечного профиля автомобильных дорог и т. д.; радиоидальная кривая и кубическая парабола используются в качестве переходной кривой, предназначенной для сглаживания резкого перехода от прямой к основной круговой кривой.
Круговая кривая характеризуется углом поворота 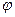 и радиусом R (рис. 62). Угол
и радиусом R (рис. 62). Угол 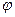 измеряется в точке В — вершине угла поворота. Радиусом R задаются с учетом нормативных требований, предъявляемых к сооружению. Главные точки кривой: НК — начало, СК — середина и КК — конец — определяются относительно вершины и направлений угла на другие вер –
измеряется в точке В — вершине угла поворота. Радиусом R задаются с учетом нормативных требований, предъявляемых к сооружению. Главные точки кривой: НК — начало, СК — середина и КК — конец — определяются относительно вершины и направлений угла на другие вер –

шины. Основные элементы кривой: Т — тангенс или касательная, Б — биссектриса, К — длина кривой, Д —домер — вычисляют по формулам

Положение средней точки можно определить также путем деления кривой на две равные части и вычисления малого тангенса t, полухорды bи стрелы f
 :
:
Основные элементы кривых выбирают из таблиц для разбивки кривых. При больших углах поворота кривая отклоняется от касательных на большое расстояние и ее разбивают кратными кривыми с углом 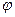 г =
г = 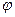 /n где п—число кратных кривых.
/n где п—число кратных кривых.
Если при разбивке кривой ее вершина недоступна (рис.63), то угол 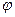 получают косвенным способом по измеренным углам
получают косвенным способом по измеренным углам 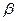 и
и  в промежуточных произвольных точках С и D. Измерив расстояние CD, решают треугольник COD иопределяют расстояния ОС и OD. Далее, задавшись радиусом круговой кривой, по углам
в промежуточных произвольных точках С и D. Измерив расстояние CD, решают треугольник COD иопределяют расстояния ОС и OD. Далее, задавшись радиусом круговой кривой, по углам 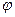 и (
и ( 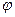 /2) находят соответственно величины Т иt. Теперь по разностям известных расстояний легко найти расстояния
/2) находят соответственно величины Т иt. Теперь по разностям известных расстояний легко найти расстояния

по которым определяют положение точек Е и F — вершины составной кривой. При этом точка Н является серединой всей кривой и точкой сопряжения кратных кривых одного радиуса. Элементы кратных кривых определяют по известной схеме. Их применяют при разбивке длинных кривых с большим углом поворота, когда кривая слишком далеко удалена от тангенса. В этом случае целесообразно делить кривую на четыре и более частей.
Детальная разбивка кривых
Положение кривой на местности не определяется полностью ее главными точками. Для строительства сооружения необходимо найти положение ряда промежуточных точек кривой. Расстояние между ними выбирают с таким расчетом, чтобы кривая

незначительно отличалась от хорды, соединяющей смежные точки. Обычно расстояние между промежуточными точками составляет 20 м при радиусе более 500 м, 10 м —при радиусе 100—500 м и 5 м — при радиусе менее 100 м. Кроме того, частота разбивки зависит от вида и материала сооружения, необходимой точности его возведения. Эти требования определяют также и точность разбивочных работ.
Существует несколько способов детальной разбивки кривых, которые различаются между собой по виду измерений и условиям использования. Разбивка кривых радиусом менее 20 м выполняется из центра кривой или при помощи шаблонов.
Способ прямоугольных координат.За ось абсцисс принимают линию тангенса (касательную), за начало координат — начало кривой для первой и конец кривой для второй ветви. Задавшись удалением k промежуточной точки кривой от начала координат (рис. 64) находят центральный угол  = (k/R)p, а по нему — прямоугольные координаты точек 1, 2,...,п:
= (k/R)p, а по нему — прямоугольные координаты точек 1, 2,...,п:

где i— текущий номер точки кривой (i=1, 2, ..., п). Вместо абсциссы часто пользуются величиной к—х. Значения у даются в таблицах и выбираются по аргументу k—х. Для разбивки точки сначала откладывают вдоль касательной величину k, а затем, отступив назад на величину k—х, фиксируют временную точку и строят в ней перпендикуляр. На нем откладывают ординату у, в конце которой закрепляют точку кривой.
Способ применяется для разбивки круговых и переходных кривых, особенно в тех случаях, когда кривая близко подходит к тангенсу, а также при выносе пикета на кривую.
Способ линейно-угловой засечки.Он заключается в построении угла  /2 в начале координат и последовательном от-
/2 в начале координат и последовательном от-

Для разбивки промежуточных точек кривой теодолит устанавливают в НК или КК. Ориентируют его по линии тангенса и откладывают от этой линии  /2. Отложив вдоль построенного направления хорду /, закрепляют первую точку. Затем в той же точке НК строят угол 2 (
/2. Отложив вдоль построенного направления хорду /, закрепляют первую точку. Затем в той же точке НК строят угол 2 (  /2) и откладывают хорду /—2, получая на пересечении направления угла и хорды точку 2, и т. д. Линейные измерения выполняют вблизи кривой, что выгодно при разбивке точек на насыпи. Если сектор угловых построений ограничен, то теодолит переносят в какую-либо определенную точку, строят в ней новую касательную и производят от нее разбивку аналогично предыдущему. Этот способ применяют для разбивки кривых земляных сооружений.
/2) и откладывают хорду /—2, получая на пересечении направления угла и хорды точку 2, и т. д. Линейные измерения выполняют вблизи кривой, что выгодно при разбивке точек на насыпи. Если сектор угловых построений ограничен, то теодолит переносят в какую-либо определенную точку, строят в ней новую касательную и производят от нее разбивку аналогично предыдущему. Этот способ применяют для разбивки кривых земляных сооружений.

Способ продолженных хорд.Задавшись длиной хорды, например 10 м, определяют смещение a = l2/R, при помощи которого разбивают все точки кривой, кроме первой. Первую точку получают по прямоугольным координатам х — 1 и у = а/2 (рис. 66). Протянув через НК (точка А) и точку 1 мерный прибор или трос длиной 21, например рулетку, на продолжении получают предварительную точку 2'. Для получения на кривой точки 2 рулетку придерживают в точке 1, а ее конец сдвигают к кривой на величину а и фиксируют точку 2. Точку 3 получают аналогично на основе линии 1—2 и далее до середины кривой. Применяется этот способ в стесненных условиях (в насыпи, выемке, шахте) при невысокой точности разбивки.
Способ трех точек.Он аналогичен способу продолженных хорд. Для хорды / вычисляют стрелу f = l2/2R, по которой определяют все точки кривой (рис. 67). Сначала разбивают точку 1 по прямоугольным координатам х = 1 и y = f. Затем рулетку или трос длиной 21 протягивают так, чтобы в точке 1 он проходил с внутренней стороны кривой на расстоянии f. В этом положении троса закрепляют точку 2, Затем начало троса переносят в точку /, укладывают его со стрелкой в точке 2 и отмечают точку 3 и далее до середины кривой.
Способ вписанного многоугольника.Он заключается в делении всей кривой на п равных частей с хордой,  где (
где ( 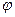 — центральный угол (рис. 68).
— центральный угол (рис. 68).
Вычислив углы  = 180°—
= 180°— 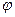 /2n
/2n  =180°—
=180°—  , начинают разбивку. Для этого теодолитом, установленным в НК (или КК) строят угол
, начинают разбивку. Для этого теодолитом, установленным в НК (или КК) строят угол  , по направлению угла откладывают хорду и фиксируют точку /. Установив на ней теодолит, строят угол
, по направлению угла откладывают хорду и фиксируют точку /. Установив на ней теодолит, строят угол  фиксируют точку 2 и далее до середины кривой. Благодаря высокой точности линейных и угловых измерений способ используется для разбивки кривых в тоннелестроении.
фиксируют точку 2 и далее до середины кривой. Благодаря высокой точности линейных и угловых измерений способ используется для разбивки кривых в тоннелестроении.
Переходные кривые
Для уменьшения вредного влияния центробежной силы и обеспечения плавности движения при переходе с прямого участка пути на кривую их сопряжение осуществляется при помощи переходной кривой. Главной особенностью переходной кривой является ее радиус, который плавно изменяется от бесконечности в начале кривой до радиуса круговой кривой.В пределах переходной кривой делают односкатный поперечный про-

Рис.69. Переходная кривая
филь (вираж) с наклоном к центру кривой (на автомобильных дорогах) или поднимают наружный рельс над внутренним (на железнодорожных линиях). Уравнение переходной кривой, выведенное из условия, чтобы в каждой ее текущей точке величина виража или возвышения рельса уравновешивала действие центробежной силы, имеет вид р = С/1, где р — радиус; I — удаление текущей точки кривой от ее начала; С—постоянная, или параметр переходной кривой. В начале переходной кривой I =0 и R=  , а в конце l = L и p = R (рис. 69), следовательно C=RL, где L — длина переходной кривой; R — радиус круговой кривой. Элементы переходной кривой определяют по формуле
, а в конце l = L и p = R (рис. 69), следовательно C=RL, где L — длина переходной кривой; R — радиус круговой кривой. Элементы переходной кривой определяют по формуле

где Т, Б, К, Д — элементы круговой кривой; Тп, Бп, Кп, Д  — элементы переходной кривой; t—дополнение к тангенсу (расстояние от НК до НПК); р — сдвижка круговой кривой.
— элементы переходной кривой; t—дополнение к тангенсу (расстояние от НК до НПК); р — сдвижка круговой кривой.
Чтобы не уменьшать радиус круговой кривой на сдвижку р, центр кривой сдвигают на величину Бр=р sec( 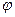 /2), где
/2), где 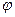 — угол поворота трассы. Поэтому тангенс круговой кривой получает приращение
— угол поворота трассы. Поэтому тангенс круговой кривой получает приращение
 .
.
Элементы переходной кривой со смещенным центром определяют по формулам

Все величины выбирают из таблиц для разбивки кривых. Пикетаж вычисляют по известному правилу.
Положение текущих точек переходных кривых задают чаще всего в прямоугольных координатах:
радиоидальная кривая (клотоида)

Для облегчения разбивки переходных кривых составлены таблицы, в которых даются прямоугольные координаты текущих точек клотоиды. Их определяют по аргументам R, L и I. Радиусы кривых приняты от 100 до 4000 м, а значения L от 20 до 200 м и кратны 10 или 20 м. Для детальной разбивки переходной кривой ее начало НПК принимают за начало координат, а тангенс — за ось — абсцисс.
Вертикальные кривые
Переломы продольного профиля дорог сопрягаются вертикальными круговыми кривыми. Различают выпуклые и вогнутые вертикальные кривые. Для обеспечения видимости на выпуклых кривых их радиусы назначаются больше, чем на вогнутых (100—30 000 м первые и 100—3000 м —вторые). Большие радиусы принимаются на железных, а меньшие — на автомобильных дорогах. Элементы вертикальных кривых определяют по радиусу и алгебраической разности уклонов (рис. 70) при помощи приближенных формул

где i 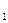 i2 — уклоны первой и второй сопрягаемых линий продольного профиля.
i2 — уклоны первой и второй сопрягаемых линий продольного профиля.
Для детальной разбивки кривых вычисляют отметки промежуточных точек профильной линии и вводят в них поправки за кривизну:


где  и
и  — отметки вершины перелома продольного профиля текущей точки кривой; х — абсцисса этой точки от начал кривой; у — поправка за кривизну, которая вводится со знаком «—» для выпуклых кривых и со знаком « + » — для вогнутых. Элементы вертикальных кривых и поправки даются в таблицах.
— отметки вершины перелома продольного профиля текущей точки кривой; х — абсцисса этой точки от начал кривой; у — поправка за кривизну, которая вводится со знаком «—» для выпуклых кривых и со знаком « + » — для вогнутых. Элементы вертикальных кривых и поправки даются в таблицах.
