Перенесение на местность проектной отметки, линии и плоскости

Одной из наиболее распространенных задач геодезии является перенесение на местность проектной отметки. Например, при закладке фундамента требуется передавать отметку на дно глубокого котлована. При укладке подземных коммуникаций, в частности, водопровода, канализации и др., необходимо передавать отметки на дно соответствующей траншеи. Кроме этого в строительстве необходимо передавать отметки на высокие части здания. Рассмотрим исходную задачу геодезии при перенесении на местность проектной отметки. Для решения данной задачи в качестве исходных данных необходимо иметь на местности доступ к известной ближайшей отметке, называемой репером. Репером, в частности, может быть соответствующий пункт высотной государственной геодезической сети. Перенести на местность требуемую отметку – значит забить в необходимую точку земной поверхности колышек, верхний срез которого будет иметь заданную высоту. Для решения задачи между репером А с отметкой Н_А и точкой В устанавливают нивелир.

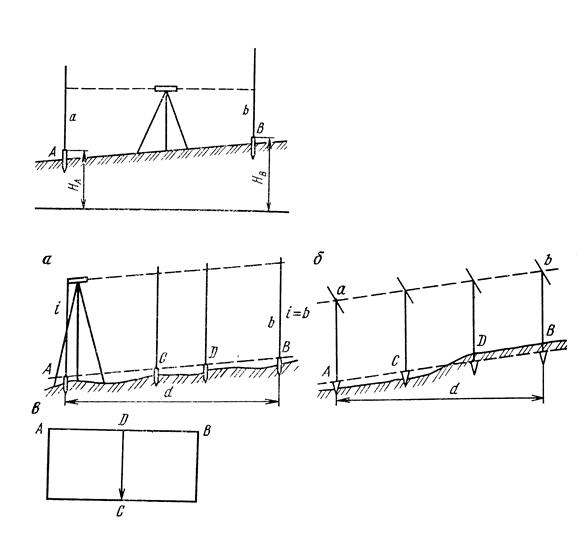
Рис. Схемы перенесения на местность наклонной линии и плоскости

По рейке, стоящей на репере, производят отсчет а. После получения отсчета а рассчитывают требуемый отсчет b = Н_А + а – Н_В. Далее в точке В забивают колышек на такую глубину, при которой отсчет по рейке, установленной на вершине колышка в точке В будет равен b. В этом случае высота пятки рейки, а следовательно и верхнего среза колышка в точке В будет равна проектной отметке Н_В.

Следующей задачей геодезии представляется задача перенесения на местность линии заданного уклона. Такая задача, например, возникает при строительстве линейных сооружений (дорог, трубопроводов). В этом случае от точки А с известной отметкой на местности Н_А откладывается длина линии АВ, равная d. После этого по известной величине уклона u находят отметку точки В по формуле: Н_В = Н_А + du. Далее в точке В забивают колышек с отметкой Н_В, так, как было рассмотрено в задаче по перенесению на местность точки с заданной отметкой. При необходимости на линии АВ разбивают промежуточные точки. Это можно сделать с помощью соответствующих расчетов отметок промежуточных точек или же с помощью наклонного луча нивелира, если превышение начальной и конечной точки невелико. Нивелир устанавливается в точке А так, чтобы один из подъемных винтов был направлен вдоль линии АВ, а линия, соединяющая два других подъемных винта, была перпендикулярна линии АВ.

При помощи подъемного винта, расположенного по линии АВ, ставят зрительную трубу нивелира на отсчет по рейке в точке В, равный высоте окуляра i. После этого в точках С и D забивают колышки такой высоты, при которой отсчеты по рейкам, установленным на верхних срезах колышков, также равнялся высоте i.

При необходимости разбивки на местности наклонной площадки в натуру, прежде всего, переносят плановое и высотное положение опорных точек А, В, С и D, определяющих границы площадки, являющихся одновременно и вершинами соответствующих квадратов.

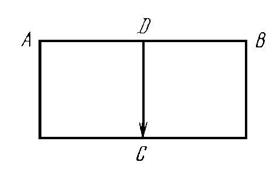
Далее на местности производят разбивку каждой опорной точки, рассмотренными выше методами. Если площадка имеет не слишком большие размеры, то её разбивку выполняют с одной станции. Для этого предварительно разбивают на местности две взаимно перпендикулярные линии АВ и СD, из которых линия СD имеет заданный уклон. На местности отметки точек А, В и D равны проектной отметке Н_D, а отметка точки С вычисляется, исходя из заданного проектного уклона площадки u. Н_С = Н_D – ud, где d – длина отрезка DC. После необходимых расчетов устанавливают нивелир в точке D так, чтобы два его подъемных винта располагались по направлению линии АВ, а третий подъемный винт – по направлению DC. Затем приводят ось вращения нивелира в вертикальное положение. При этом отсчеты по рейкам в точках А и В должны равняться высоте окуляра прибора i. Затем, визируя зрительную трубу на реку, установленную в точке С, вращают третий подъемный винт до тех пор, пока отсчет по рейке не станет равным i, то есть высоте прибора. При такой установке нивелира визирная ось трубы при вращении будет всегда находиться в плоскости, параллельной проектной плоскости наклонной площадки. Далее необходимо забить в требуемых точках колышки так, чтобы отметки их верхних срезов соответствовали высоте прибора.

Передача отметок на дно глубокого котлована и на высокие части сооружения.В строительной практике необходимо передавать соответствующие отметки вниз, например, на дно глубокого котлована, глубина которого часто превышает длину геодезической рейки. В таких случаях для передачи отметки требуется два нивелира, один из которых установлен на поверхности земли, а другой размещен на дне котлована или на соответствующем монтажном горизонте.

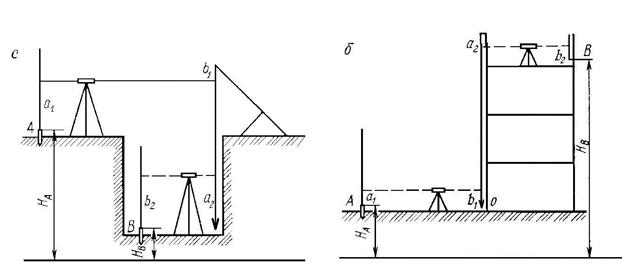
Рис. Схемы передачи отметок на дно глубокого котлована и высокие части сооружения

Для передачи отметки на дно глубокого котлована над котлованом устанавливают кронштейн, к которому подвешивают рулетку с грузом на нулевом конце. Далее берут отсчет а₁ по рейке, установленной в точке А на соответствующем репере. После этого поворачивают зрительную трубу верхнего нивелира в сторону подвешенной рулетки и берут отсчет по рулетке b₁. По второму нивелиру, установленному на дне котлована, берут отсчет по рулетке а₂. Далее нивелировщик, находящийся на дне котлована, направляет зрительную трубу нивелира на рейку, установленную на вершине колышка в точке В и делает отсчет по рейке b₂. Зная отметку Н_А репера в точке А, можно рассчитать отметку В, то есть высоту верхнего среза колышка, находящегося на дне глубокого котлована, по формуле:

H_B = H_A + a₁ – (b₁ – a₂) – b₂;

Для того, чтобы отметка НВ равнялась проектной отметке, отсчет по рейке, установленной на дне котлована должен составлять величину b₂ = H_A + a₁ – (b₁ – a₂) – H_B. Имея расчетное значение отсчета b₂, на дне котлована забивают временный знак, верхний срез которого перемещают по вертикали до тех пор, пока отсчет по соответствующей рейке не совпадет с расчетной величиной.

Процесс передачи отметки на высокую часть здания, по сути, аналогичен перенесению отметки на дно котлована. Рассмотрим данную задачу на примере. Допустим, что необходимо передать отметку от репера А на репер В соответствующего монтажного горизонта. Отметка репера В рассчитывается по формуле:

H_B = H_A + a₁ + (a₂ – b₁) – b₂; Определив отметку репера В, на стене сооружения отмечают проектную отметку, закрепляя её одним из известных способов.

Разбивка на местности круговых кривых.При строительстве линейных сооружений, например, дорог, трубопроводов и др, появляется необходимость перенесения на местность круговых кривых. Разбивка круговой кривой начинается с расчетов и разбивки на местности так называемых главных точек кривой. Этими точками, в частности, являются начало кривой, конец кривой и середина кривой.

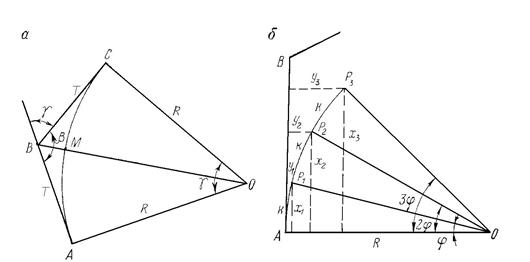
Рис Схемы разбивки главных точек кривой и детальной разбивки кривой способом перпендикуляров

Для определения этих точек требуется знать угол поворота γ = 180 – β, радиус кривой R, длину касательной АВ = ВС = Т, называемой тангенсом, длину кривой АМС = К, биссектрису ВМ = Б. Угол β измеряется с помощью теодолита в точке В, радиус R задается, исходя из технических нормативов для проектирования сооружений. После расчета γ можно вычислить значения Т = R·tg γ/₂; Б = ВО – МО = R(1/cos γ/₂ – 1); K = π Rγ/180; Для практических расчетов элементов кривой созданы специализированные таблицы, в которых по аргументам γ и R можно подобрать значения Т, Б и К. Отложив на местности от вершины угла поворота В величины отрезков ВА = ВС = Т, а вдоль биссектрисы угла отрезок Б, получим координаты начала кривой (НК), конца кривой (КК) и середины кривой (СК). При строительстве зачастую появляется необходимость разбивки не только главных точек кривой, но и промежуточных точек, что позволяет выполнять работы с повышенной точностью. В зависимости от требований решения задачи промежуточные точки кривой располагаются между главными точками через 2, 5, 10 или 20 метров. Наименьший интервал устанавливается для кривых малого радиуса, находящегося в пределах от 20 до 100 метров. Наибольший интервал при радиусах кривой 1000 метров и более. Чаще всего в практике строительства детальную разбивку круговых кривых выполняют, используя способ прямоугольных координат. Для этого способа, как известно, требуется открытая площадка. Перед выносом соответствующих точек на местность необходимо рассчитать положение точек Р₁, Р₂, Р₃ и … так, чтобы расстояния между ними по кривой были равны К. Условно примем касательную АВ за ось абсцисс Х, а соответствующий перпендикулярный оси АВ радиус R за ось ординат Y. При этом положение точек Р₁, Р₂, Р₃, лежащих на заданной кривой можно определить с помощью прямоугольных координат. Для этого рассчитаем вначале численное значение угла φ, соответствующего длине дуги k, показанной на рисунке. φ = 180^О·k/(π·R). Из рисунка следует, что x₁ = R·sin φ; y₁ = R(1 – cos φ) = 2R·sin²(φ/2); Аналогично определяются координаты точек Р₂, Р₃, … Р_n, а именно: x₂ = R·sin2φ; y₂ = 2R sin²(2φ/2); x₃ = R· sin3φ; y₃ = 2R sin²(3φ/2); … x_n = R·sin nφ; y_n = 2R·sin²(nφ/2); Абсциссы и ординаты откладывают на местности по касательной и по перпендикуляру к ней с помощью теодолита и мерной ленты. Разбивку кривой производят от начала и конца кривой к её середине. Координаты промежуточных точек можно брать не только из расчетов, но и из соответствующих таблиц для разбивки круговых кривых.

Таблица детальной разбивки круговой кривой радиуса 100 м

Точки кривой	Расстояния НК и КК	Координата Х	Координата У
Р1		9,98	0,50
Р2		19,87	1,99
Р3		29,55	4,47
Р4		38,94	7,89