Арифметическая средина. средняя квадратическая ошибка. предельная и относительная ошибки

Исходя из четвертого свойства случайных ошибок при геодези­ческих измерениях одинаковой точности, за окончательный ре­зультат принимают среднее арифметическое из ряда измерений.Если измерена одна и та же величина п раз и получены результаты: l₁, l₂, l₃, ..., l_n, то

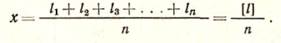(12)

Величина х называется арифметической срединой или вероят-нейшим значением измеренной величины.

Разности между каждым измерением и арифметической сре­диной называются вероятнейшими ошибками измерений:

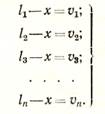(13)

Сложив равенства (13), получим

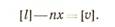(14)

Из формул (12) и (14) следует, что [υ] = 0.

Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

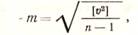(15)

где [и²] — сумма квадратов вероятнейших ошибок; п — число из­мерений.

Средняя квадратическая ошибка арифметической средины вычисляется по формуле:

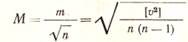(16)

Предельная ошибка не превышает утроенной средней квадратической ошибки, т. е.

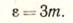(17)

Пример.* Линия измерена шесть раз. Определить ее вероят-нейшую длину и оценить точность этого результата. Вычисления приведены в табл. 1.

Таблица 1

№ п/п	Длина линии, м	υ, СМ	υ2	Вычисления
	225,26 225,23 225,22 226,14 225,23 225,12	+6 +3 +2 -6 +3 -8		т=√158/(6-1)=5,6см М=5,6/√6=2,3см
хср = 225,20	[υ] = о	[υ2] = 158

По формулам (15) и (16) вычислены абсолютные средние квадратические ошибки, а оценивать точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная ошибка вероятнейшего значения изме­ренной линии равна

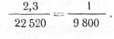
СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ОШИБКА ФУНКЦИЙ ИЗМЕРЕННЫХ ВЕЛИЧИН

Если мы имеем функцию суммы или разности двух независимых величин

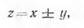(18)

то квадрат средней квадратической ошибки функции выразится формулой:

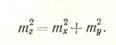(19)

При т_х = т_у = т

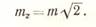(20)

Пример. Линия на плане масштаба 1:5000 измерена по частям. Одна часть длиной 600,5 м, вторая часть длиной 400,0 м. Найти средние квадратические ошибки суммы и разности этих длин и соответствующие им относительные ошибки.

Ответ. Средняя квадратическая_ошибка суммы и разности двух длин будет т_г =0,7 м, где т = 0,5-точность масштаба. Относительные ошибки суммы и разности длин соответственно равны

0,7/1000,5=1/1 400 и 0,7/200,5=1/300

Если функция имеет вид

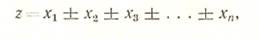(21)

то

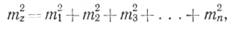(22)

т. е. квадрат средней квадратической ошибки алгебраической суммы аргументов равен сумме квадратов средних квадратиче-ских ошибок слагаемых.

Если m₁ = m₂ = m₃ = .. . = m_п= m. то формула (22) примет вид

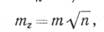(23)

т. е. средняя квадратическая ошибка алгебраической суммы (разности) измеренных с одинаковой точностью величин в √п раз больше средней квадратческой ошибки одного слагаемого.

Пример. В шестиугольнике каждый угол измерен с одинаковой точностью 0,5', средняя квадратическая ошибка суммы всех измеренных углов будет

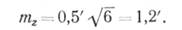
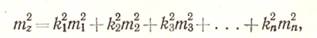(24)

то

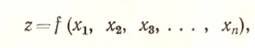
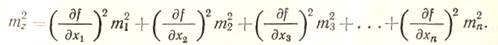(27)

Из формулы (27) следует, что квадрат средней квадратической ошибки функции общего вида равен сумме квадратов произведений частных производных по каждому аргументу на среднюю квадратическую ошибку соответствующего аргумента.