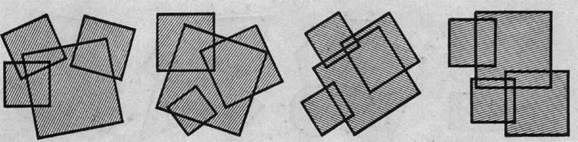
Плоскостные композиции из ряда прямоугольников
Понятия и сложности выявления конструктивных начал в доступной форме, многие пытаются решить задачи конструктивизма интуитивным или опытным порядком.

Четвертой причиной малой популярности конструктивных начал необходимо признать то обстоятельство, что в распоряжении лиц, готовых уделить достаточное внимание вопросам конструктивизма, не имеется конкретного материала, могущего осветить данный вопрос. Нет источника, который мог бы дать исчерпывающие данные тем, кто хочет ознакомиться с конструкциями. Каждому интересующемуся обоснованием, логикой и сущностью конструктивизма, приходится самому подбирать себе материал из массы разнородных опытов и фактов, и на основе этого материала строить свою собственную систему с логическим обоснованием ее.

 |
Несмотря на все указанные причины, затрудняющие удовлетворение потребности в конструктивном творчестве, эта потребность все же постоянно заявляет о себе. Искание конструктивных начал
 |
| 14 15 16 17 |
Плоскостные композиции из ряда квадратов 
 |
заложено по существу в каждом живом существе и особенно резко выражено в деятельности человека. Человеку врожденобыть во всех областях жизни строителем, и это чувствуется с первых же моментов его существования. Ребенок, не получая никаких указаний извне, часто сам решает во время своих игр и занятий довольно сложные вопросы конструктивизма. Например, следует признать, что всякий узел (из нитки, веревки и т. д.) и всякое скрепление (пало чек, щепочек и т. д.) есть по существу конструкция; следовательно, можно обнаружить конструкцию в самых примитивных детских затеях, например, когда ребенок при помощи палочек вполне рационально решает вопрос подпорок, защемления одной части в другой, когда он занимается шитьем платьев для кукол и т. д. Не строить, не создавать человек не может, — отсюда появляется необходимость иметь дело с конструкцией предмета. Это происходит непроизвольно —стихийно. То обстоятельство, что в первой стадии своего развития ребенок любит разрушать, следует признать также характерным явлением, так как почти всякому творческому процессу обычно предшествует разрушение. Всякий, открывший нечто новое, разрушает что-то, ранее выработанное, установившееся, вовсе не будучи по своему характеру абсолютным разрушителем. Видимо,
 |
 |
18 19 20 21
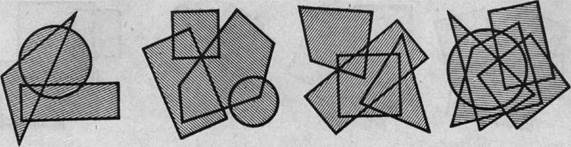
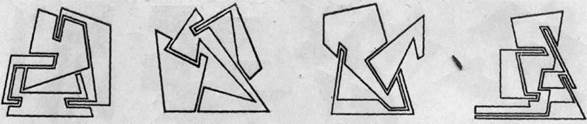
Плоскостные композиции из различных фигур 
природа человека устроена так, что вслед за разрушением он приступает к созиданию.
Безотчетная потребность в конструктивизме, хотя бы бессистемном, присущая каждому человеку, в конечном результате должна
в будущем найти себе основу. Эта основа должна быть формулирована в доступном, ясном виде и должна уяснять всю сложную систему
конструктивизма.

 |
Нельзя не подчеркнуть некоторых особенностей, сопровождающих искание конструктивных начал у отдельных, склонных к этому, лиц. Эта потребность выражается довольно ярко в целом ряде работ экспериментального порядка и носит характер изобретательства. Никто не станет отрицать того, что всякий изобретатель технического типа наделен от природы склонностью к конструктивным началам. Мы не предрешаем вопроса о том, как у каждого индивида выражается способность отображать конструкцию —наглядным или объемно-пространственным путем, или графически, —
 |
 |
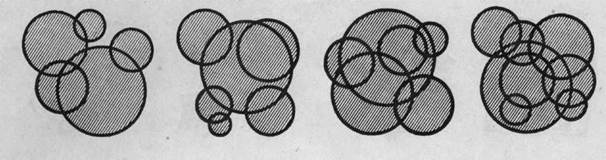
Плоскостные композиции из ряда кругов 
22 23 24 25
мы только констатируем наличие факта, что многим лицам свойственно от природы обладать конструкторскими качествами. Потребность человека в конструировании окружающих его жизнь объектов властно диктует поиски рационального и здорового выхода из неясного и неопределенного положения. И мощное строительство, и грандиозная техника нашего времени столь быстрым темпом идут вперед, что в окружении их человеку необходимо осознать, понять и изучить все этапы, законы, свойства конструктивизма. Не только хочется знать основы конструктивизма, но надо их знать. Иными словами: потребность в знании начал конструктивизма стала потребностью времени.

 |
Особенно настойчиво проявляются искания конструктивизма за последнее время в Германии и Голландии, наблюдаются они и в СССР, хотя следует заметить, что ни на Западе, ни у нас еще не было сделано попытки систематизации идей конструктивизма, не было сделано точной, исчерпывающей характеристики его законов и воз
 |
 |
 \
\
26 27 28 29
Прозрачныекомпозиции а) изквадратов, Ь) из прямоугольников, с) из прямоугольныхполос, d) из различных фигур
можностей. Ясно лишь одно: конструктивизм, как художественное направление, стремится к созданию синтеза техники и всех видов изобразительных искусств в единой форме конструктивистического творчества, которое „строится соответственно принципам механического, геометрического и эстетического взаимоотношений материала конструкций (краска, полотно, железо, стекло и т. д.) и ее форм" (определение И. Маца в книге „Искусство современной Европы"). Следует отметить особенность нашего века, заключающуюся в том, что стремлением к конструктивизму заражено множество людей. Эта зараженность отдельных индивидов — более глубокое явление, чем можно предположить. Потребность отдельных лиц, разных по существу специальностей, ищет себе выхода, создает особое состояние, вызывающее необходимость выявить сущность конструктивных замыслов. Люди ищут: этим самым предопределяется будущность того, что ищут. Человечество, став на путь исканий, во всех почти случаях добивается, если не полного ответа на них, то известного успеха. Самый факт существования многочисленных попыток оформить конструктивые начала говорит за то, что
 |

 |
Пространственные композиции из ломаных плоскостей 
30 31 32 33
вопрос о конструктивизме назрел и действительно является „потребностью".
 |
Не представляя собою науки высшего порядка, учение о конструктивизме, безусловно, в недалеком будущем примет доступные и понятные формы, приближающие его ко всем тем, кто пожелает заняться изучением конструктивных начал.
Как верно замечает Б. Арватов („Искусство и классы"), конструктивизм есть не форма, а метод. „Поскольку этот метод подлежит коллективизации, поскольку он кладет в основу принципы социально технического использования материалов, поскольку, наконец, он ставит своей прямой задачей организацию не только идей и людей, но и вещей, —постольку конструктивизм является историческим движением, переходным от искусства вне жизни стоящих, закоснелых форм к искусству социально-жизненному, к эволюционно-динамическому, т, е. к искусству пролетарскому".

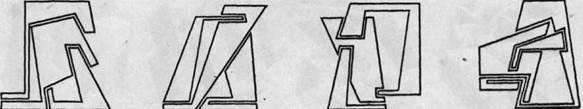 |
 | |||||
 |  |
 35 35    |
 |
Статические решения соче
В.СМЫСЛ КОНСТРУК ТИВИЗМА  |
Тания неправильных фигур
 |
Смысл конструктивизма таится в сути всех конкретных начал, которые он обслуживает. Сама по себе конструкция может существовать и без обязательной оправданности ее применения, но тогда ценность ее понижается, и ее удельный вес становится небольшим в сравнении с действительной ее значимостью. Совершенно другую картину мы наблюдаем в том случае, когда видим не только тесное объединение объема и конструкции, но рациональный смысл этой связи. Разве у нас не „открываются глаза" в том случае, когда мы в едином цельном куске-теле обнаруживаем признаки конструктивизма (рис. 85)? Мы убеждаемся на столь простом примере в наличии „конструкции", как таковой. Данный простой объем делается, благодаря конструктивности, „осмысленным". Приведенный пример — самый простой. Во всех случаях конструирования сооружения можно усмотреть определенный смысл связи одного тела с другим. Можно предлагать много различных решений какой-нибудь части сооружения, они будут раз
 |
    |
 |
Статические решения соче таниянеправильных фигур
ниться между собою, но мы во всех случаях будем предлагать „конструктивное" решение. Это значит, что, создавая здание, мы решать его будем конструктивным путем.

 |
Машина говорит сама за себя во всех случаях своего выявления. Машина не может быть не конструктивна, так как она воплощает в себе все виды и начала конструктивизма. Наилучшие примеры конструктивных начал и основ мы наблюдаем в машине и ее деталях. Но, помимо конструирования предметов тяжелых-компактных, существует еще конструкция мягких тел и поверхностей. К числу таких объектов следует отнести одежду человека. Смысл подобной конструкции зиждется в самой структуре одеяния и потребности в ней. Если сейчас одежда человека не достигла совершенства, то это следует объяснить несовершенством самой жизни людей, многими
 |
| 42 43 44 45 |

Пространственноконструктивные сочетанияпрямоугольных плоскостей 
Экономическими и бытовыми недочетами. В будущем человек окружит себя столь законченными предметами обихода и быта, что поневоле сосредоточит свое внимание на одеянии, вполне пригодном к самым различным функциям. Постепенно происходят уже теперь сдвиги в этом направлении, хотя бы в вопросах физкультуры.

 |
Самый смысл конструктивизма во всех случаях заключается в том, что он создает впечатление необходимости увязки одного элемента с другим. Наблюдая функциональную зависимость ряда объектов между собою и оправдывая эту зависимость, мы, тем самым, утверждаем тот конструктивный рационализм, к которому стремимся. Смысл конструктивизма таится также и в том, что он создает у нас убеждение в той устремленности обхвата, каким обладают некоторые предметы. В цепком сочленении и спаянности отдельных элементов между собою есть узаконение принципа сцепления. Когда одно тело внедряется в другое и, тем самым, порождает
 |
46 47 48 49

 Пространственно-конструк
Пространственно-конструк
тивные сочетания овальных плоскостей 
зависимость одной части от другой, то в совокупности их взаимодействия создается законченное произведение. Мы и тут обнаруживаем смысл, заключающийся в том, что коллективные объединения ряда элементов образуют одно определенное целое. В то время, как отдельный элемент представляет собою нечто безличное в общей массе, группа конструктивно-объединенных элементов представляет собою оформленную единицу, т. е. определенное и целостное единство.

 |
Еще лучше мы убеждаемся в смысле конструктивизма, когда сталкиваемся с такими вопросами практического характера, где только конструктивным путем может быть решена та или иная задача. В сооружениях таких движущихся машин, как паровоз, аэроплан, автомобиль, пароход и пр., смысл всех конструктивно-спаянных частей свидетельствует об особой, строго рассчитанной комбинации всех элементов. И поскольку все осмысленно в таких машинах,— постольку они логичны.


Композиция вертикальных и горизонтальных линий разных толщин с участием фигуры квадрата 

Композиция вертикальных и горизонтальных линий раз личных толщин 

Композиция вертикальных, горизонтальных и наклонных прямых с участием фигур круга 
Самым интересным моментом является в конструктивизме его рациональность. Без этого свойства конструктивизм не мыслим. Соединение таких значительных и важных начал, как конструктивизм и рациональность, говорит об осмысленности рассматриваемого нами вопроса.
 |
Наконец, из простого наблюдения конструктивных предметов и сооружений ясно, что конструктивизм является необходимой потребностью и постоянной принадлежностью всего уклада нашей жизни и что без конструктивных начал немыслимо разрешить большинство вопросов техники и искусства.
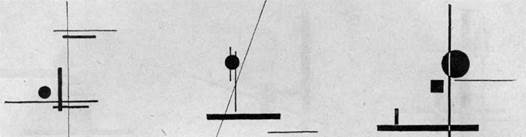

Композиция равновесия конструктивно - связанных прямых с пятном круга

Композиция равновесия прямых с пятном круга и длинного прямоугольника 


