Исследование гидравлического
ПРЫЖКА
1. ЦЕЛЬ РАБОТЫ
Определить вид гидравлического прыжка, его длину, потери энергии в прыжке.
Сравнить опытные величины h", Lnp с вычисленными по формулам.
Определить состояния потока до и после гидравлического прыжка.
Вычислить значения прыжковых функций П(h') и П(h'').
2. ОБЩИЕ СВЕДЕНИЯ
Гидравлическим прыжком называется резкое увеличение глубины потока от величины h', меньшей hKp, до величины h", большей hKp. Это явление наблюдается на относительно коротком участке русла (рисунок 3.1) и является единственной формой перехода потока из бурного состояния в спокойное.
Глубины h' и h" измеряемые в сечениях 1-1 и 2-2, ограничивающих прыжок, называются сопряженными. Расстояние между этими глубинами называется длиной гидравлического прыжка Ьпр. Высота гидравлического прыжка ап - это разность между второй и первой сопряженными глубинами, т. е. ап = h"—h'. В потоке между сечениями 1-1 и 2-2 наблюдается поверхность раздела АВС; ниже этой поверхности струя (транзитная струя) резко расширяется от глубины h' до глубины h"; выше поверхности АВС имеется поверхностный валец, который представляет собой водоворотную область, насыщенную пузырьками воздуха.
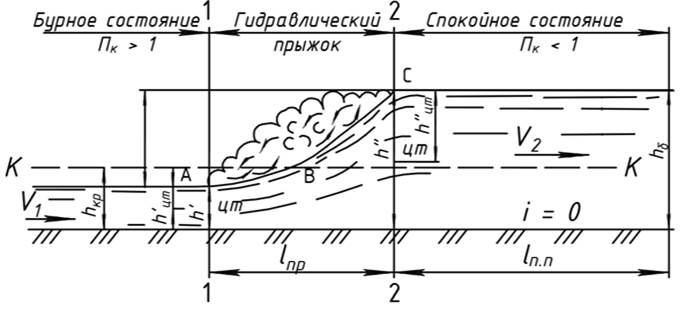
Рисунок 3.1 - Схема гидравлического прыжка
В зависимости о.т условий, в которых происходит гидравлический прыжок, наблюдаются различные его виды: совершенный, волнистый, подпертый, затопленный, поверхностный и другие гидравлические прыжки.
Совершенный гидравлический прыжок образуется в нестесненном русле при уклоне дна близком к нулю и соотношении сопряженных глубин h''/h' ≥2. В прыжке этого вида заметно выражены поверхностный валец и транзитная часть потока.
Другие виды гидравлических прыжков подробно описаны в справочной литературе.
Состояние потока (бурное, спокойное, критическое) характеризуется параметром кинетичности Пк. Параметр кинетичности выражает количественное соотношение кинетической и потенциальной энергий и определяется отношением удвоенной кинетической энергии к потенциальной энергии потока
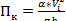 , (3.1)
, (3.1)
где α - коэффициент Кориолиса, α ≈ 1,1;
V - средняя скорость потока в сечении, м/с;
h - средняя глубина в том же сечении потока, м.
При Пк < 1 поток находится в спокойном состоянии (h>hKp); при Пк> 1 - поток в бурном состоянии (h<hKp) ; при Пк = 1 - поток в критическом состоянии (h = hKp).
Для русла прямоугольного поперечного сечения с уклоном дна равным нулю и однородной шероховатостью уравнение гидравлического совершенного прыжка имеет вид:
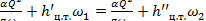 , (3.2)
, (3.2)
где Q - расход воды в лотке, м3/с;
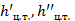 - глубины погружения центров тяжести соответственно первого и второго живых сечении потока, м;
- глубины погружения центров тяжести соответственно первого и второго живых сечении потока, м;
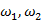 - площади живых сечении потока в первом и втором створах соответственно с глубинами h'' и h', м2.
- площади живых сечении потока в первом и втором створах соответственно с глубинами h'' и h', м2.
Левая часть уравнения (3.2) равна правой. Следовательно, выражение (3.2) можно записать как
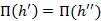 , (3.3)
, (3.3)
где 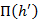 - прыжковая функция первой сопряженной (взаимной глубины;
- прыжковая функция первой сопряженной (взаимной глубины;
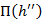 - прыжковая функция второй сопряженной (взаимной глубины;
- прыжковая функция второй сопряженной (взаимной глубины;
Сопряженные глубины в прямоугольном русле (лотке) гидравлического совершенного прыжка находятся по формулам
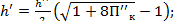 (3.4)
(3.4)
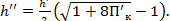 (3.5)
(3.5)
Потери энергии в совершенном гидравлическом прыжке в прямоугольном русле определяются из выражения
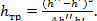 (3.6)
(3.6)
Длина совершенного гидравлического прыжка для прямоугольного русла определяется по эмпирическим формулам. Наиболее часто используется формула Н.Н. Павловского.
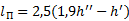 . (3.7)
. (3.7)
3. ОПИСАНИЕ УСТАНОВКИ
На рисунке 1.1 представлена схема опытной установки. Вода из трубопровода 1 поступает в приемную камеру 3. При помощи задвижки 2 регулируется расход воды на водосливе 5 и в лотке 6. Пьезометр 4, установленный на внешней стороне камеры 3, используется для измерения напора на водосливе. В начале лотка имеется специальный паз 8, в который вставляется плоский вертикальный затвор. В конце лотка имеется паз 7 для установки щита, служащего для изменения состояния потока между затвором и щитом.
4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Открывается задвижка 2 и устанавливается свободное истечение из-под затвора, установленного в пазе 8 лотка 6. Щитом в конце лотка создается подпор так, чтобы в лотке образовался гидравлический прыжок. Маневрируя щитом в пазе 7, устанавливается гидравлический прыжок примерно на середине лотка.
При помощи шпиценмасштаба измеряются отметки уровня воды и дна лотка в начале и конце гидравлического прыжка (сечение 1-1 и 2-2 на рисунке 3.1). Уклон дна лотка равен нулю.
Расход воды определяется с помощью водослива-водомера 5 по тарировочной кривой Q =f(H).
Длина прыжка измеряется сантиметровой линейкой.
Результаты измерений и расчетов заносятся в таблицу 3.1.
5. ПОРЯДОК ВЫЧИСЛЕНИЯ
1. Определяется глубина воды в первом и во втором сечениях:
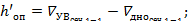
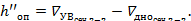
2. Находятся параметры кинетичности потока до и после гидравлического прыжка:
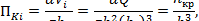
где 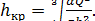
3. Вычисляется вторая сопряженная глубина h'' из формулы (3.5):
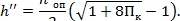
4. Находятся прыжковые функции 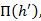
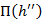 :
:
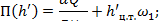
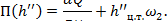
Таблица 3.1 - Опытные данные
| Наименование | Опыты | |
| 1. Расход по тарировочной кривой Q, м3/с | ||
| 2. Отметка дна в сеч. 1-1 ,м | ||
| 3. Отметка уровня воды в сеч. 1 -1, м | ||
| 4. Отметка дна в сеч. 2-2, м | ||
| 5. Отметка уровня воды в сеч. 2-2, м | ||
| 6. Ширина потока лотка, м | ||
| 7. Глубина перед прыжком h'on, м | ||
| 8. Глубина за прыжком h"on, м | ||
| 9. Параметр кинетичности до прыжка П'к | ||
| 10. Параметр кинетичности после прыжка П"к | ||
| 11. Прыжковая функция П(h) | ||
| 12. Прыжковая функция П (h") | ||
| 13. Глубина за прыжком h"по формуле (3.5), м | ||
| 14. Вид прыжка | ||
| 15. Длина прыжка по замерам lпр, м | ||
| 16. Длина прыжка по формуле (3.7) lпр, м | ||
| 17. Потери энергии в прыжке hmp, м |
5. Определяется вид гидравлического прыжка.
6. Вычисляется длина прыжка по формуле (3.7).
7. Находятся потери энергии из выражения (3.6).
8. По данным табл. 3.1 в масштабе 1:5 вычерчивается совершенный гидравлический прыжок.
9. Сравнить опытные результаты по длине гидравлического прыжка с расчетной длиной, полученной из формулы (3.7). Сделать вывод.
ЛАБОРАТОРНАЯ РАБОТА №4
